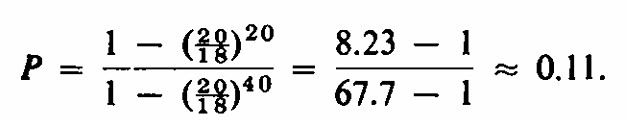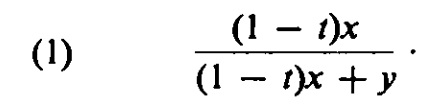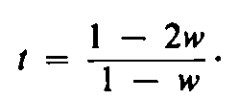En Las Vegas, un hombre con $20 necesita $40, pero le da vergüenza pedirle más dinero a su esposa. Decide invertir en la ruleta (aunque no le gusta jugar) y está considerando dos estrategias: apostar los $20 de una vez en los números pares y dejar de jugar si gana o pierde, o apostar $1 a la vez en los números pares hasta ganar o perder $20.

Compara los méritos de las estrategias

Solución

El juego audaz, como lo llaman Lester E. Dubins y Leonard J. Savage en su libro Cómo apostar si es necesario,(véase artículo esp) es decir, apostar $20 de una vez, le da una probabilidad de

18/38 ≈ 0.474

de alcanzar su objetivo (En la ruleta americana, hay 38 casillas en total: 18 son rojas, 18 son negras, y 2 son verdes (0 y 00).

Un juego cauteloso, un dólar a la vez, nos lleva al problema de la ruina del jugador con

m=20                    n=20

p=18/38        q=20/38

que da una probabilidad ≈ 0.11 .

El juego cauteloso ha reducido sus posibilidades  menos de una cuarta parte de las del juego audaz.

La explicación intuitiva es que el juego audaz también es un juego rápido, y el juego rápido reduce la exposición del dinero al porcentaje de la casa. Hemos visto varias veces que las intuiciones basadas en promedios no siempre conducen a probabilidades correctas. Dubins y Savage advierten que no se conoce ninguna prueba de los méritos del juego audaz, en general, que esté basada en este argumento intuitivo.

Sin embargo, Dubins señala que para nuestro caso especial de duplicar el dinero en el juego de Rojo-y-Negro, la siguiente exposición de Savage sí se basa en esto.

Al preparar esta discusión para nosotros, Savage ha pasado por alto deliberadamente un par de puntos matemáticos sutiles relacionados con la alcanzabilidad de límites.

El Paraíso Dorado
En el Paraíso Dorado venden cualquier apuesta justa en la que un jugador tenga fondos para apostar.

Un jugador que entra al Paraíso Dorado con x dólares con el objetivo de ganar y dólares adicionales, si es posible, puede lograr su objetivo con una probabilidad de x/(x + y) apostando toda su fortuna x en una única oportunidad de ganar y con una probabilidad de x/(x + y), lo cual es claramente justo. Como es bien sabido, ninguna estrategia puede darle una mayor probabilidad de alcanzar su objetivo, y la probabilidad es tan alta solo si se asegura de perder x o ganar y eventualmente.

El Paraíso Menor
El Paraíso Menor se parece al Paraíso Dorado con la importante diferencia de que antes de salir del salón, el jugador debe pagar un impuesto sobre la renta del 100t% (0<t<1) sobre cualquier ingreso neto positivo que haya ganado allí.

Por lo tanto, no es ni más difícil ni más fácil para él ganar y dólares con una fortuna inicial de x de lo que es para su hermano en el Paraíso Dorado ganar y/(1 - t) dólares. La mayor probabilidad con la que puede lograr su objetivo es, por lo tanto,

El Paraíso Perdido

Aquí, el crupier recauda el impuesto de 100t% sobre el ingreso positivo, si lo hay, de cada apuesta individual.

El jugador aquí evidentemente no está en mejor situación que su hermano en el Paraíso Menor.

En particular, (1) es un límite superior en la probabilidad de ganar y con una fortuna inicial de x en el Paraíso Perdido.

Esta probabilidad se puede alcanzar apostando todo en una única oportunidad como antes. Sin embargo, no se puede lograr mediante ninguna estrategia que tenga una probabilidad positiva de emplear alguna apuesta que tenga una probabilidad positiva de ganar cualquier cantidad positiva menor que y después de impuestos.

Para ver esto, considera que el hermano del Paraíso Menor puede imitar cualquier estrategia del hermano del Paraíso Perdido, reservando para su propio uso posterior lo que el crupier tome del hermano del Paraíso Perdido en impuestos sobre pequeños premios. Así, el primero puede tener un ingreso esperado más alto que el que pueda tener el último en cualquier estrategia en la que arriesgue ganar un pequeño premio.

Rojo y negro

En Rojo-y-Negro, el jugador puede apostar cualquier cantidad que posea contra una probabilidad w (0 < w < 1/2) de ganar un premio igual a su apuesta. Dicho de otra manera, gana el premio justo de (1 - w)/w veces su apuesta, sujeto a un impuesto inmediato del 100t% donde

Por lo tanto, la probabilidad de que un jugador en Rojo-y-Negro gane y con una fortuna inicial de x es como máximo (1), al igual que para su hermano en el Paraíso Perdido. En términos de w, esto es