43. La Barra Rota

Problema 43 del libro de Mosteller

Una barra se rompe al azar en dos lugares. Encuentra el tamaño promedio del más pequeño, del tamaño mediano y del más grande de los pedazos.

Solución para La Barra Rota

Podemos trabajar con una barra de longitud unitaria. Sea x y y las posiciones de los dos puntos de ruptura, x el más a la izquierda (Fig. 1). Sabemos por el principio de simetría que cada uno de los tres segmentos (izquierda, medio y derecha) promedia ¹/₃ de la longitud en caídas repetidas de dos puntos. Pero se nos pregunta sobre el más pequeño, por ejemplo. Si dejamos caer dos puntos al azar, sea X la posición del primer punto dejado caer y Y la del segundo. Luego el par aleatorio (X, Y) se distribuye uniformemente sobre un cuadrado unitario.

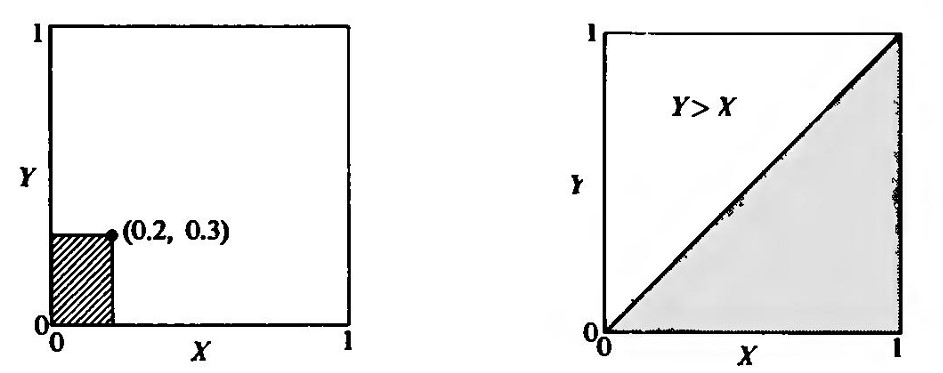
Figura 1. Intervalo con puntos de ruptura x e y.

Continúa la solución

Dejemos que X represente la posición del primer punto dejado caer y Y la posición del segundo. Luego el par aleatorio (X, Y) se distribuye uniformemente sobre un cuadrado unitario como en la Fig. 2, y las probabilidades se pueden medir por áreas. Por ejemplo, la probabilidad de que X < 0.2 y Y < 0.3 está dada por el área debajo y a la izquierda de (0.2, 0.3), y es 0.2 × 0.3 = 0.06.

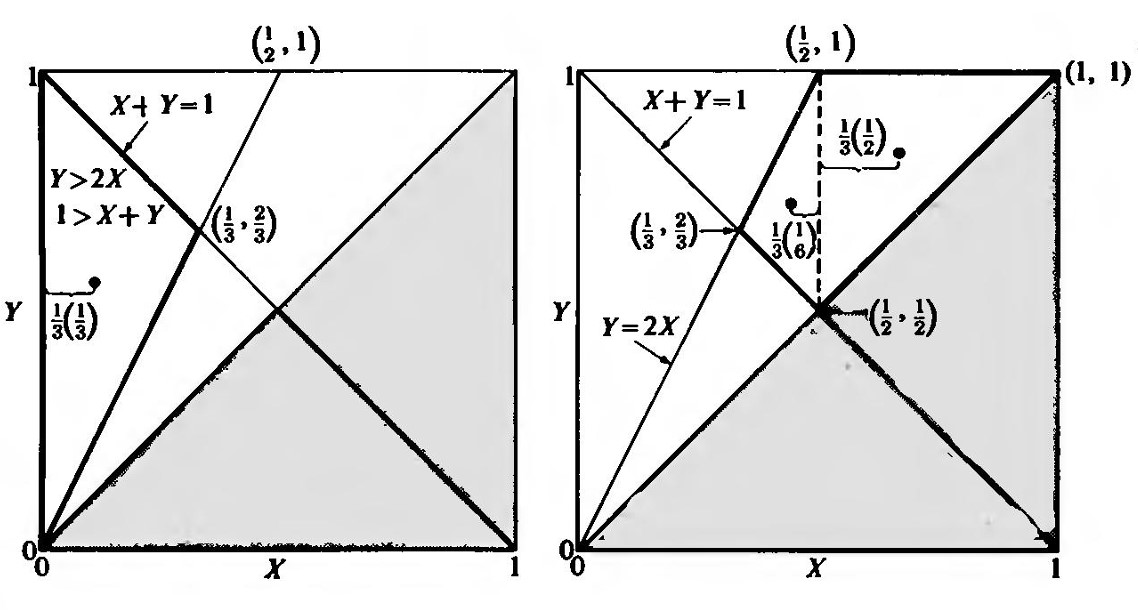
Fig. 2. Cuadrado unitario que representa la distribución de probabilidad para un par de puntos (X, Y) dejados caer en un intervalo unitario.

Fig. 3. El área sin sombrear muestra donde Y > X.

Por conveniencia, supongamos que X está a la izquierda de Y, o que X < Y. Luego, la distribución está sobre la media cuadrícula sin sombrear en la Fig. 3. Las probabilidades aún son proporcionales a las áreas, pero el área debe multiplicarse por 2 para obtener la probabilidad. Si queremos obtener la longitud promedio del segmento de menor tamaño, entonces observe que cualquiera de X, Y - X, o 1 - Y es el menor. Supongamos que X es el menor, de modo que

X < Y - X o, equivalentemente, 2X < Y,

y

X < 1 - Y o, equivalentemente, X + Y < 1.

En la Fig. 4, la región triangular que cumple todas estas condiciones se muestra fuertemente delineada. Aunque X varía de 0 a ¹/₃, debe promediarse sobre la región triangular. El hecho clave de la geometría del plano es que el centroide de un triángulo está a ¹/₃ de la distancia desde una base hacia el vértice opuesto. La base de interés en el triángulo delineado es la que está en el eje Y. La altitud paralela al eje X es ¹/₃. En consecuencia, el promedio de X es ¹/₃ × ¹/₃ = ¹/₉. Por lo tanto, el valor promedio del segmento más pequeño es ¹/₉.

Veamos qué pasa si X es el más grande. Queremos

X > Y - X o, equivalentemente, 2X > Y,

y

X > 1 - Y o, equivalentemente, X + Y > 1.

La Fig. 5 muestra la región cuadrilátera apropiada fuertemente delineada. Para obtener su promedio para X, rompemos la región cuadrilátera en dos triángulos como se muestra.

Fig. 4. Región triangular donde el segmento más pequeño es más pequeño está fuertemente delineada.

Fig. 5. Región donde X es el más grande está fuertemente delineada.

Luego calculamos el promedio para X para cada triángulo por separado y ponderamos los dos promedios por las áreas de los triángulos para obtener la respuesta final. El promedio de X para el triángulo derecho cuya base es la línea de puntos es

¹/₂ +¹/₃ ·¹/₂

El del triángulo izquierdo cuya base es la línea de puntos es

¹/₂ - ¹/₃ ·¹/₆

Los pesos son proporcionales a las alturas ¹/₂ y ¹/₆

respectivamente, porque los triángulos tienen una base común.

Finalmente, el promedio de X es

[¹/₂(¹/₂ + ¹/₆) + ¹/₆(¹/₂ - ¹/₁₈)] / (¹/₂ + ¹/₆) = ¹¹/₁₈

Dado que el promedio del más pequeño es ¹/₉ o ²/₁₈ y que para el más grande es ¹¹/₁₈, el promedio para el segmento del medio es 1 - ¹¹/₁₈ - ²/₁₈ = ⁵/₁₈. Puede verificar esto aplicando el método que acabamos de usar cuando, por ejemplo, 1 - Y > X > Y - X.

Finalmente, los promedios del segmento más pequeño, del tamaño mediano y del más grande de la barra rota son proporcionales a 2, 5 y 11, respectivamente.

Cuando rompemos una barra en 2 pedazos, los tamaños promedio de los pedazos más pequeños y más grandes son proporcionales a

¹/₄, ³/₄, lo que se puede escribir como ¹/₂(¹/₂), ¹/₂(¹/₂ + 1).

Para 3 pedazos tenemos, en orden, las proporciones

¹/₃, ⁵/₁₈, ¹¹/₁₈,

o

1/3(¹/₃), 1/3(¹/₃ + ¹/₂), 1/3(¹/₃ + ¹/₂ + ¹/₁).

En general, si hay n piezas, las longitudes promedio en orden de tamaño son proporcionales a

más pequeño:

¹/_n ( ¹/_n )

siguiente más grande:

¹/_n ( ¹/_n + ¹/_n-1 )

tercero:

¹/_n ( ¹/_n + ¹/_n-1 + ¹/_n-2 )

...

más grande:

¹/_n ( ¹/_n + ¹/_n-1 + ... + ¹/₂ + 1 )

Pero no tengo una prueba fácil de esto.

Créditos
Traducción del problema 43 del libro Fifty Challenging Problems in Probability with Solutions,  F.  Mosteller,  Dover, New York, 1965 , MOSTELLER

Vídeo introducción con lumen5.com