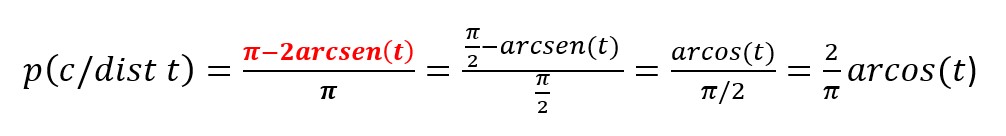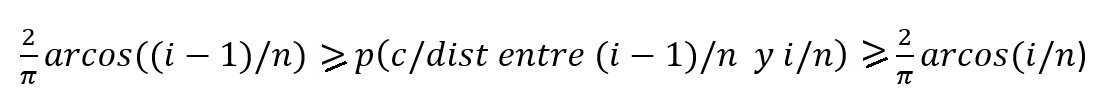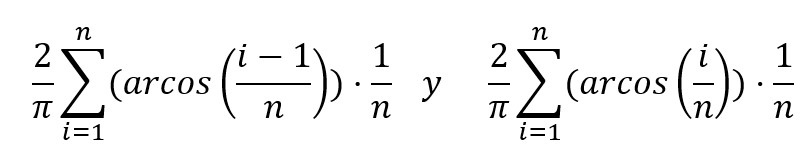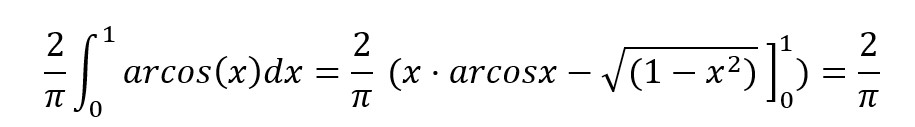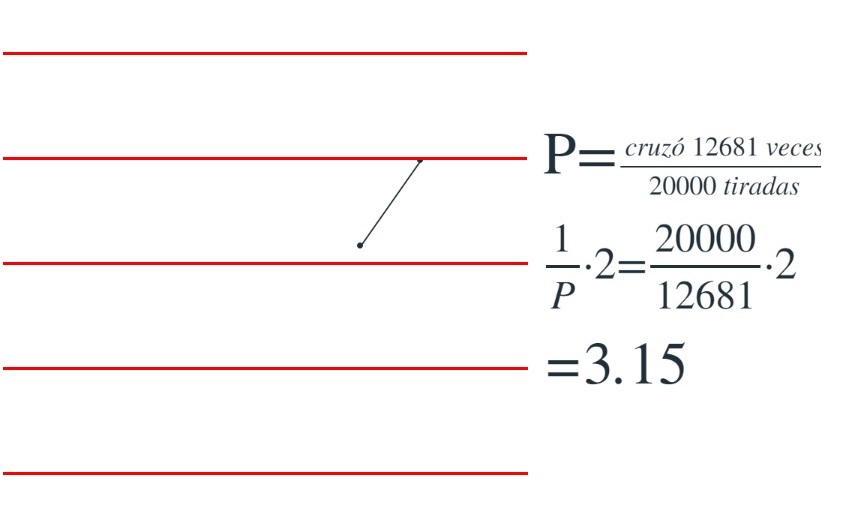Aguja de Buffon

El problema de la Aguja de Buffon conecta la geometría con la teoría de la probabilidad. Aunque su solución está altamente documentada, nuestra meta es abordarlo de manera que sea accesible para estudiantes de segundo de bachillerato.

Imagina un suelo entarimado con tablas de madera dispuestas en líneas paralelas, separadas por una distancia de 2 unidades cada una. Ahora, lanzamos un palillo de longitud 2 unidades sobre este suelo. El desafío es demostrar que la probabilidad de que el palillo cruce alguna de las juntas entre las tablas es exactamente 2/π.

Este enigma, aparentemente simple nos invita a explorar la relación entre la geometría y la probabilidad estimulando el razonamiento matemático. Acompáñanos mientras desentrañamos los secretos de la Aguja de Buffon y nos sumergimos en el apasionante mundo de las matemáticas.

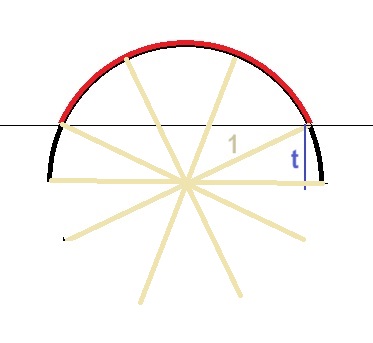
1 Calculemos la probabilidad de que el palillo cruce alguna de las juntas (suceso c) sabiendo que su centro está a una distancia t de la junta que tiene más cerca (suceso dist t). Hallaremos p(c/dist t)

Estando el centro del palillo a una distancia t de la junta, los casos favorables para cada lugar del centro son los que el extremo cae en la parte señalada en rojo y los casos posibles son toda la semicircunferencia,

2 Calculemos la probabilidad de que el centro del palillo esté a menos de una distancia t de la junta más cercana

los casos favorables son aquellos señalados en rojo, su área es 2t· ancho· número de juntas = 2t· ancho· largo/2 (pues 2 es la distancia entre dos juntas). Por tanto los casos favorables ocupan un área igual a t· ancho· largo

3 Probabilidad de que la mínima distancia del centro del palillo a una junta sea entre (i-1)/n y (i/n) siendo n un número natural y i también número natural pero menor o igual que n

Esta probabilidad es igual a 1/n

4 Probabilidad que el palillo cruce una junta sabiendo que la mínima distancia de su centro a una junta está entre (i-1)/n y (i/n)

Como la distancia del centro a la junta más cercana será mayor que (i-1)/n y menor que i/n pues según el punto 1 esta probabilidad, p(c/ dist entre (i-1)/n y (i/n)) está acotada por los valores de p(c/dist (i-1)/n) y p(c/dist i/n):

5 La probabilidad de que cruce una junta y la mínima distancia del centro a una junta esté entre entre (i-1)/n y (i/n)

Esta probabilidad es el producto de la condicionada, calculada en el punto 4 y la probabilicad calculada en el punto 3, luego está comprendida entre

Por último la probabilidad de que el palillo cruce alguna junta es igual a las suma de estas probabilidades cuando i varía de 1 a n, pues el centro estará en alguna de las franjas, así pues estará comprendida entre

Se ha hecho una simulación del experimento para ver cuanto se tarda en alcanzar ese valor de 2/pi
y después de realizar 20000 tiradas se ha obternido para la inversa de la probabilidad de cruzar una junta multiplicada por 2 un valor igual a 3,15 que aún dista de pi una centésima

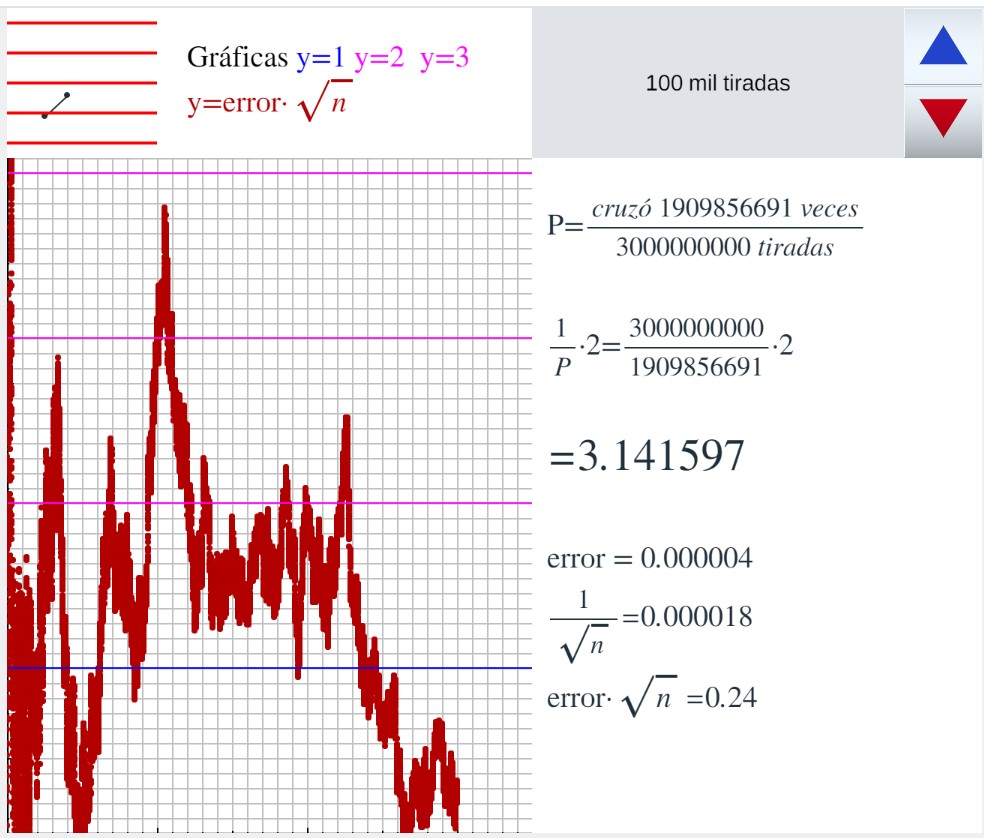
Y la imagen muestra los resultados obtenidos después de más de 1000 millones de tiradas,

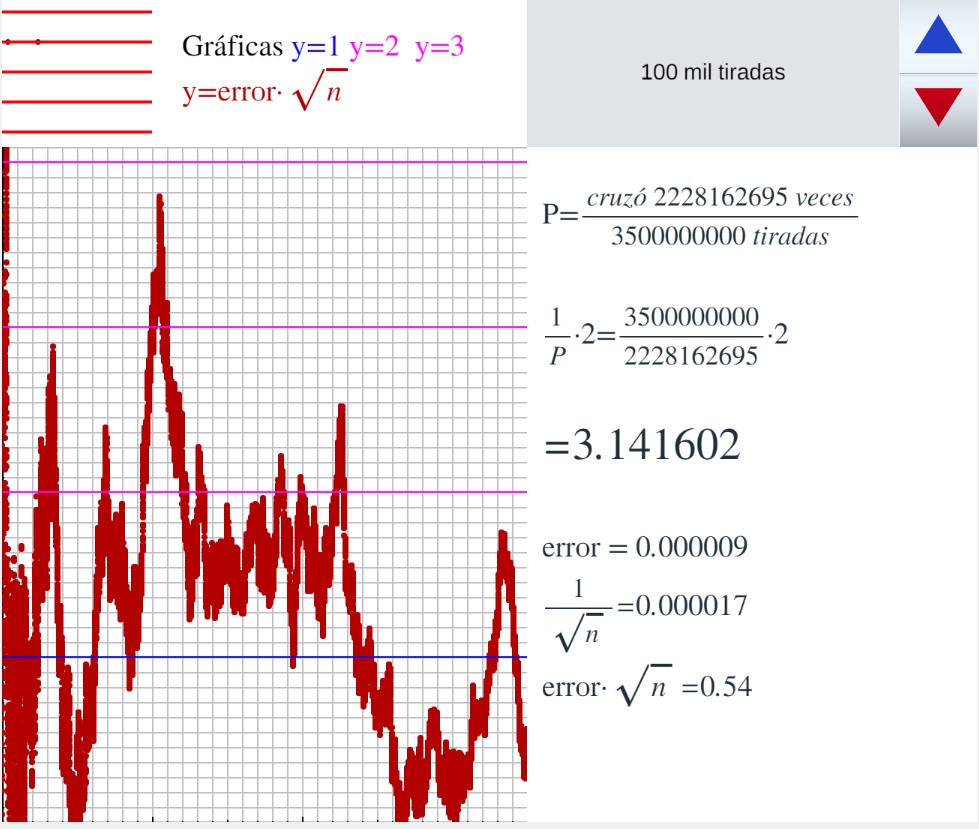
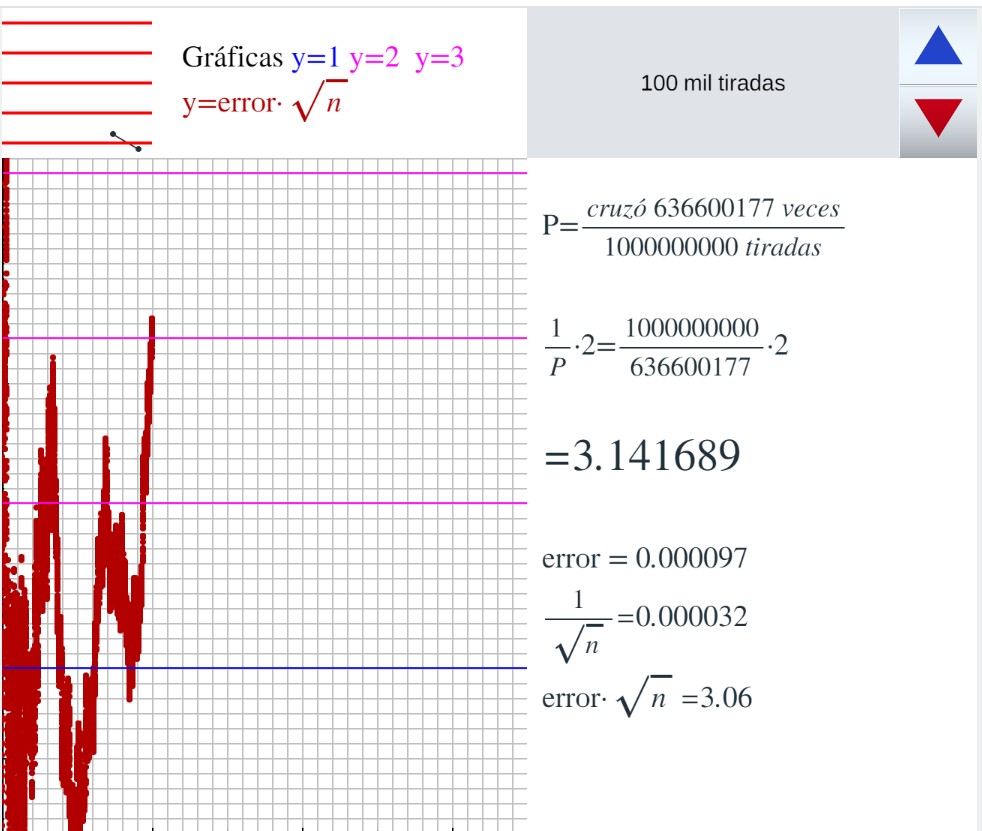
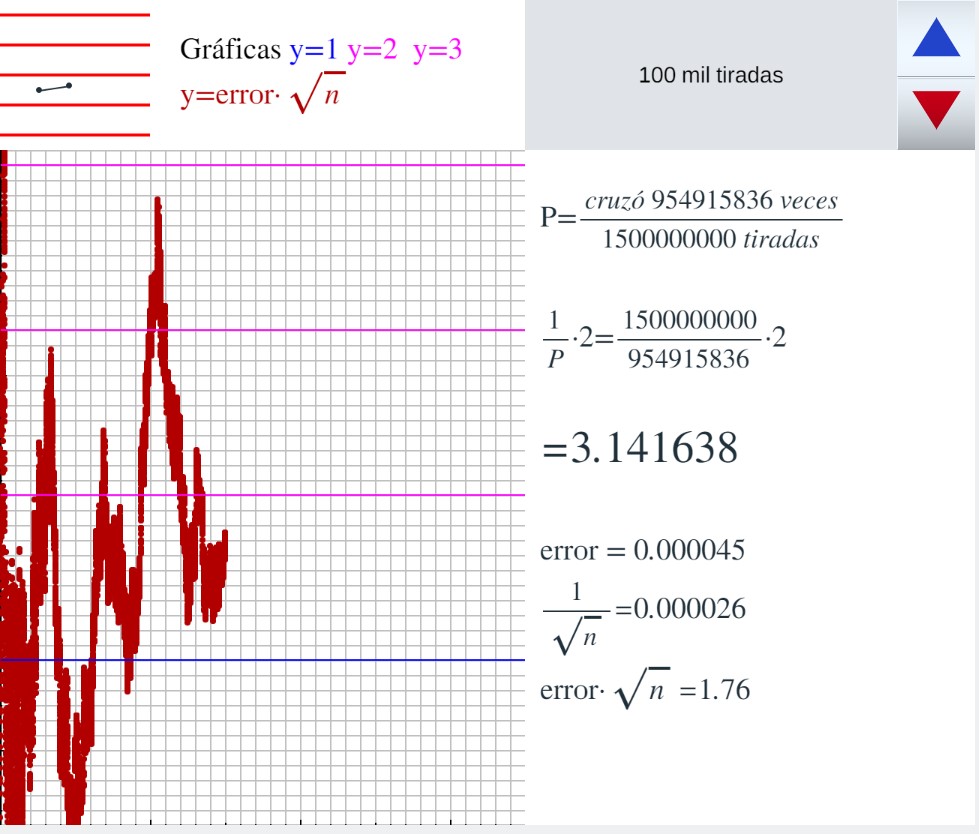
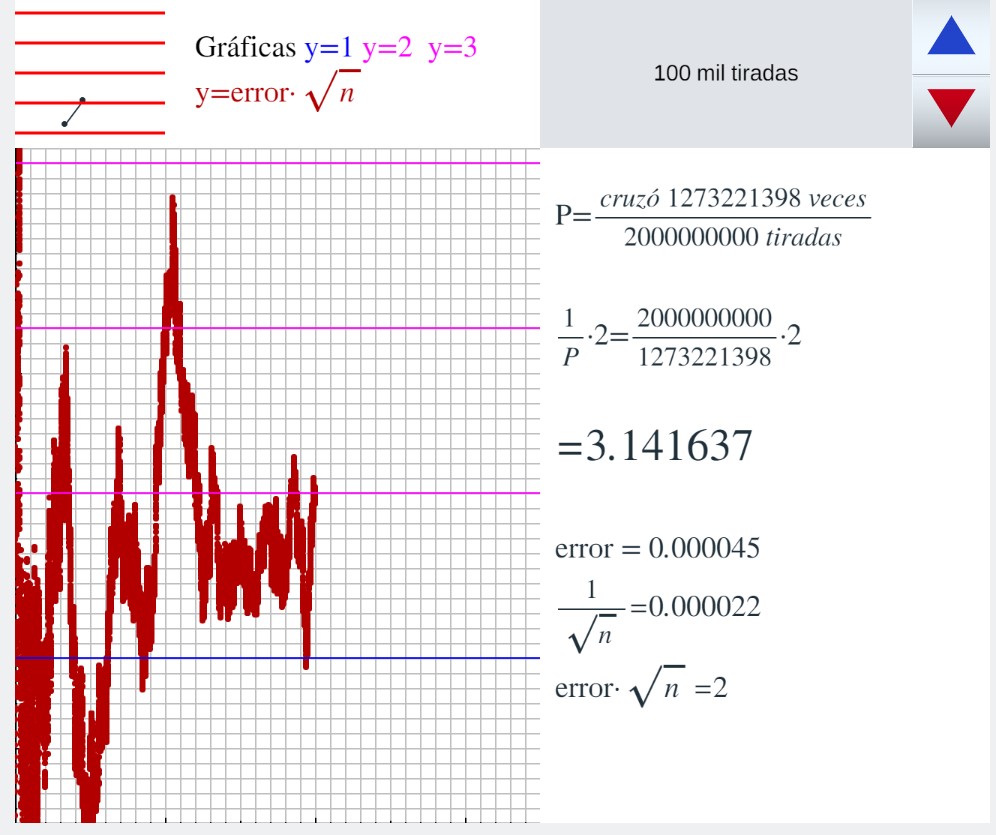
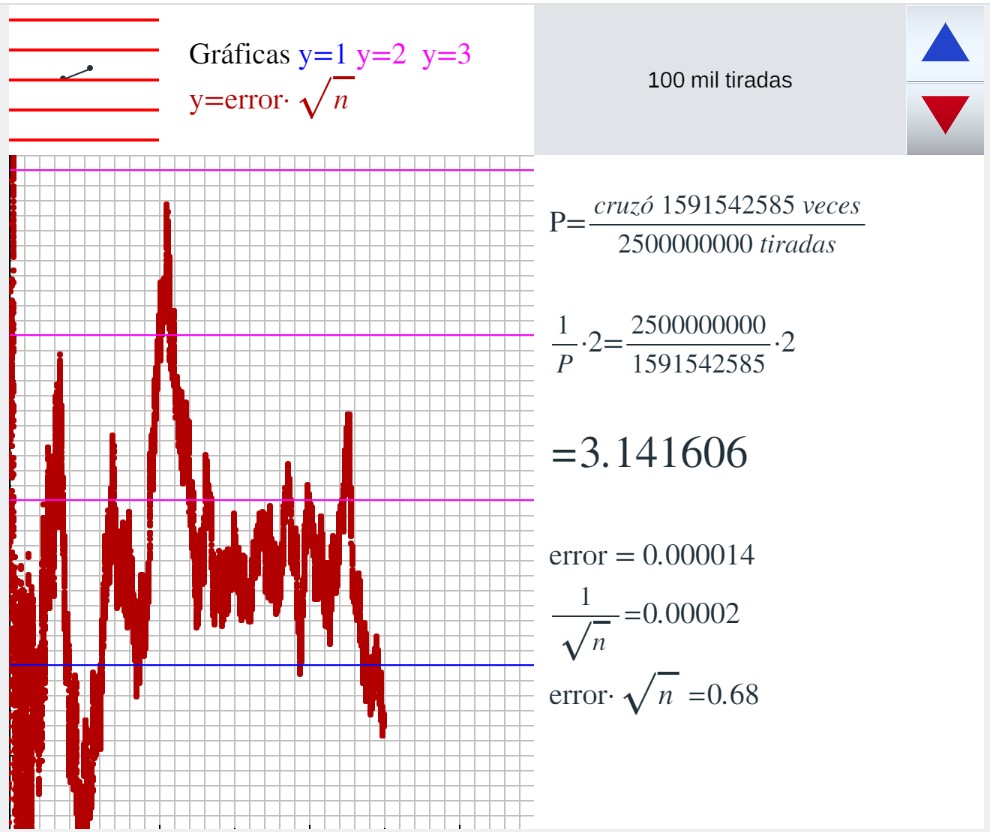
Comparación del error en la aproximación de pi por las agujas de Buffón con 1/raíz(n)

En una escena de Descartes se simula el experimento de la aguja de Buffon, cada vez que se presiona el triángulo azul o el rojo se realizan 100 mil tiradas. Se van dibujando en marrón los puntos (n, error/(1/raíz(n)) es decir, (n, (pi-2n/c)·raíz(n)) solo se dibuja uno de cada 100000 puntos

Con ella se ha realizado un experimento de 3500 millones de tiradas, la captura del resultado final ha sido

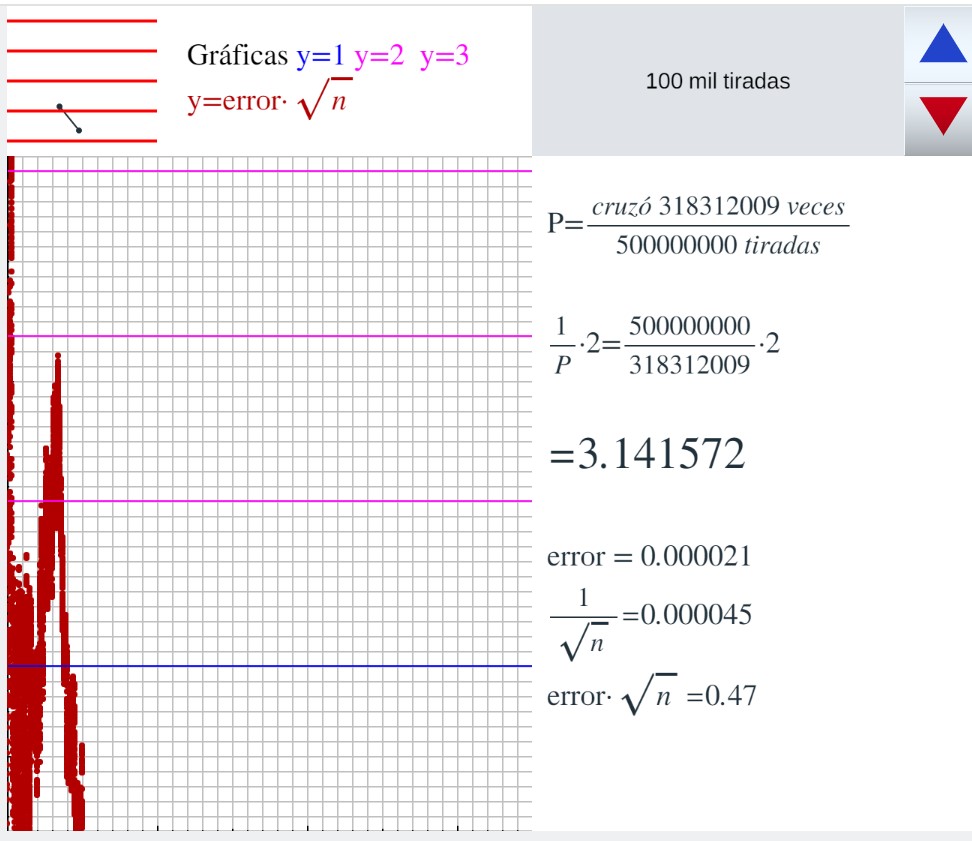
Sucesivos videos del experimento

La siguiente escena es similar, al presionar el triángulo azul se realizan 10^4 lanzamientos. Esta permite más cosas, así en un fondo anaranjado se ve la gráfica de todos los valores obtenidos en los primeros 10^6 lanzamientos, (los puntos marrones son solo los últimos en cada pulsación, si no se modifica nada, será un punto de cada 10^4 lanzamientos). También permite cambiar el número de lanzamientos en cada pulsación (control tiradas), o la amplitud del eje x (expo), o comparar el error con k/raíz(n) (control k) o con otra potencia de n (control potn) Estos controles aparecen cualdo se hace clic derecho sobre la escena. Los controles n1 y c1 nos servirán para ampliar las tiradas, supongamos que la amplitud es como al inicio, 10^7 (expo=7) , pues después de 10^7 lanzamientos, si anotamos los valores n=10^7 como n1 y el c obtenido como c1, entonces al pulsar inicio, modificar n1 y c1 con los valores obtenidos y cerrar, la gráfica será continuación de la anterior, es decir podemos ver como saldrán los siguientes 10^7 lanzamientos.