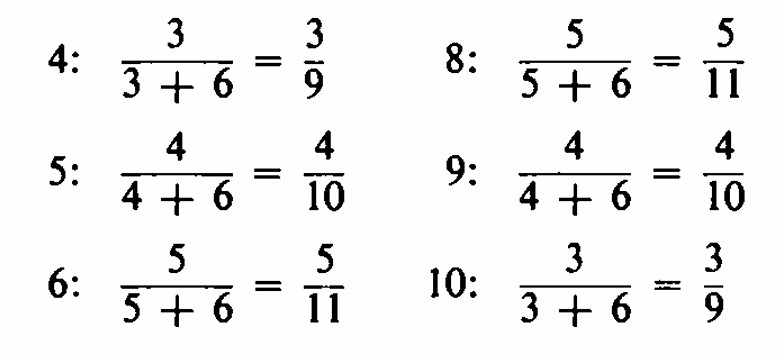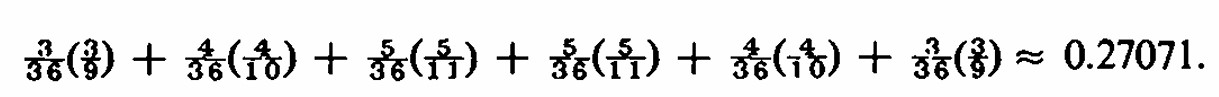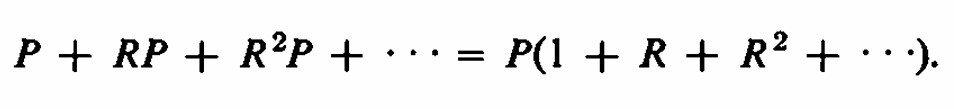|
Craps Solo cuentan los totales de los dos dados. El jugador lanza los dados y gana de inmediato si el total de la primera tirada es 7 u 11, pierde de inmediato si es 2, 3 o 12 Cualquier otra tirada se llama su " punto . " Si la primera tirada es un punto, el jugador tira los dados repetidamente hasta que gane volviendo a sacar su punto o pierda tirando un 7. ¿Cuál es la probabilidad de ganar del jugador?
Solución
El juego es sorprendentemente equitativo, como veremos, pero ligeramente
en desventaja para el jugador.
Primero obtengamos las probabilidades para los totales de los dos dados.
Consideremos los dados como distinguibles, digamos rojo y verde.
Entonces hay 6 × 6 = 36 posibles lanzamientos igualmente probables cuyos
totales se muestran en la tabla dado rojo
Al contar las celdas en la tabla obtenemos la distribución de probabilidad de los totales:
Por lo tanto, la probabilidad de ganar en el primer lanzamiento es P ( 7 ) + P ( 11 ) = (6+2) /36 = 8/36 La probabilidad de perder en el primer lanzamiento es P ( 2 ) + P ( 3 ) + P ( 12 ) = (1+2+1) /36 = 4/36 Para los lanzamientos posteriores necesitamos la probabilidad de hacer el punto. Dado que no hay lanzamientos excepto el punto o el 7 que importen, podemos calcular para cada uno de estos la probabilidad condicional de hacer el punto dado que se ha lanzado inicialmente. A veces, este enfoque se llama el método de espacios de muestra reducidos porque, aunque los lanzamientos reales producen los totales del 2 al 12, ignoramos todo excepto el punto y el 7. Por ejemplo, para cuatro como punto, hay 3 formas de hacer el punto y 6 formas de hacer un siete, por lo que la probabilidad de hacer el punto es 3 / (3 + 6) = 3/9. De manera similar, obtenemos las probabilidades condicionales para los otros puntos y resumimos:
Cada probabilidad de ganar debe ser ponderada por la probabilidad de lanzar el punto en el lanzamiento inicial para obtener la probabilidad incondicional de ganar para ese punto. Así, la probabilidad de ganar lanzando un punto es la suma
A esto le sumamos la probabilidad de ganar en el primer lanzamiento, 8/36 ≈ 0.22222, para obtener 0.49293 como la probabilidad del jugador de ganar. Su pérdida esperada por unidad apostada es 0.50707 - 0.49293 = 0.01414 , 1.41 % . Creo que este es un juego de inicio equitativo que no tiene estrategia . Y el 1.4 % no suena como mucho , pero mientras escribo , las acciones de General Motors se están vendiendo a 71 , y su dividendo anual ( antes de extras ) se cita como $ 2 , o aproximadamente 2.8 % . Entonces, por cada dos jugadas en los dados, tu pérdida es igual al pago de dividendos anuales de la corporación más grande de Estados Unidos . Algunos lectores pueden no estar satisfechos con el enfoque de probabilidad condicional utilizado para los puntos y pueden desear ver la serie sumada . Sea P la probabilidad de lanzar el punto y sea R la probabilidad de un lanzamiento que no cuenta, R=1−P-1/6 Este 1/6 es la probabilidad de lanzar un 7. El jugador puede ganar lanzando una serie de lanzamientos que no cuentan y luego lanzando su punto . La probabilidad de que haga su punto en el (r+1)º lanzamiento (después del lanzamiento inicial) es Rr·P , r = 0 , 1 , 2 , . . . Para obtener la probabilidad total , sumamos los valores de r
Sumando esta serie geométrica infinita obtenemos Probabilidad de hacer punto = P / ( 1 − R ) . Por ejemplo si el punto es 4, P=3/36 R=1-3/36-6/36=27/36 (1 − R)=9/36 P / (1 − R) = 3/9 como obtuvimos mediante el enfoque más simple de espacios muestrales reducidos . Mosteller comenta: "La primera vez que me encontré con este problema , sumé la serie y estaba bastante satisfecho conmigo mismo hasta que unos días después se me ocurrió el enfoque de espacios muestrales reducidos y me quedé desanimado ."
Créditos Vídeo introducción con lumen5.com Simulación del craps realizada con chatGPT
Consolación Ruiz Gil Abril 2024 https://www.matsolin.com/craps/index.htm
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||