50. Ecuaciones Cuadráticas Aleatorias

Problema del libro de Mosteller

¿Cuál es la probabilidad de que la ecuación cuadrática

tenga raíces reales?

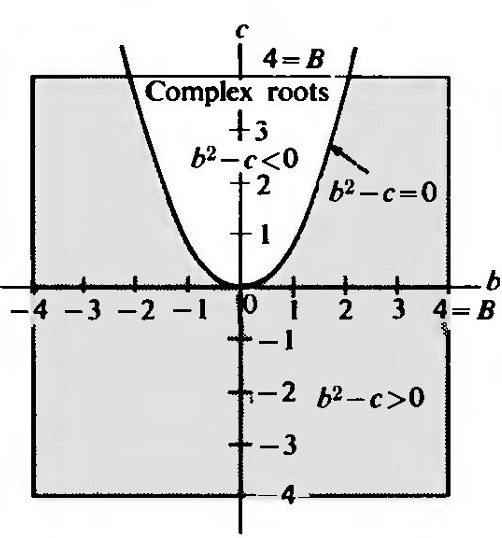
Solución para Ecuaciones Cuadráticas Aleatorias

Para hacer esta pregunta significativa, supondremos que el punto \((b, c)\) se elige al azar de una distribución uniforme sobre un gran cuadrado centrado en el origen, con lado \(2B\) (ver la figura). Resolvemos el problema para un valor dado de \(B\); luego dejamos que \(B\) crezca lo suficientemente grande para que \(b\) y \(c\) puedan tomar cualquier valor.

Para que la cuadrática tenga raíces reales, debemos tener

En la figura, trazamos la parábola \(b^2 = c\) y mostramos las regiones en el cuadrado, para \(B = 4\), donde la ecuación original tiene raíces reales.

Es un ejercicio fácil en cálculo mostrar que el área de la región sin sombrear es \(\frac{4}{3}B^3\) (para \(B \geq 1\)), y, por supuesto, el área del cuadrado completo es \(4B^2\). En consecuencia, la probabilidad de obtener raíces complejas es \(1/(3\sqrt{B})\). Cuando \(B = 4\), el resultado es \(\frac{1}{6}\). A medida que \(B\) crece, \(1/\sqrt{B}\) tiende a cero, y por lo tanto la probabilidad de que las raíces sean reales tiende a 1!

Debo advertirles que el problema que acabamos de resolver no es idéntico a aquel para \(ax^2 + 2bx + c = 0\). Podrías pensar que podrías dividir por \(a\). Puedes, pero si los viejos coeficientes \(a, b, c\) se distribuyeron independientemente y uniformemente sobre un cubo, entonces \(b/a\) y \(c/a\) no son ni uniformemente ni independientemente distribuidos.