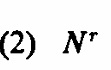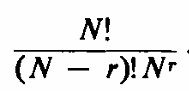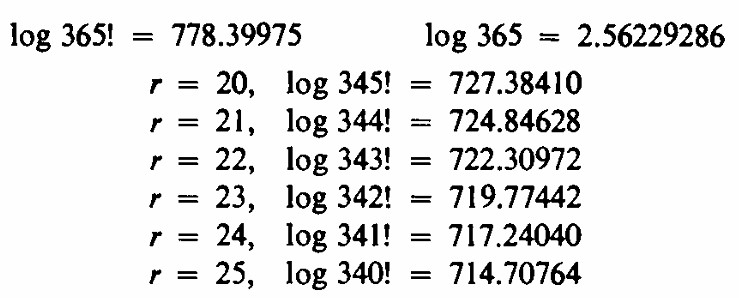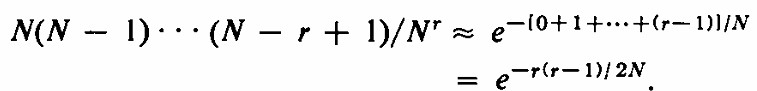Cuál es el número mínimo de personas requerido si la probabilidad supera que dos o más de ellas tengan el mismo cumpleaños (No es necesario que el año de nacimiento coincida)

Solución

Las simplificaciones habituales son que se ignora el 29 de febrero como una posible fecha de cumpleaños y que los otros 365 días se consideran fechas de cumpleaños igualmente probables.

Resolvamos un problema algo más general.

Sea N el número de días igualmente probables,

r el número de individuos,

y calculemos la probabilidad de que no haya cumpleaños iguales.

Luego podemos obtener la probabilidad de al menos un par de cumpleaños iguales tomando el complemento.

Hay N días para que la primera persona tenga un cumpleaños,

N-1 para el segundo para que no coincida con el primero,

N - 2 para el tercero para que no coincida con ninguno de los dos primeros,

y así sucesivamente hasta N - r + 1 para la r-ésima persona.

Multiplicamos y encontramos el número de formas en que no haya cumpleaños iguales

Para obtener la probabilidad de no tener cumpleaños iguales también necesitamos el nú mero de formas en que r personas pueden tener cumpleaños sin restricciones.

Hay N formas para cada persona. Entonces el número total de formas diferentes en que se pueden asignar los cumpleaños a r personas es

El número en la expresión ( 1 ) dividido por el de la expresión ( 2 ) es la probabilidad de no tener cumpleaños iguales, porque asumimos que todos los cumpleaños y, por lo tanto, todas las formas de asignar cumpleaños son igualmente probables.

El complemento de esta proporción es la probabilidad de al menos un par de cumpleaños iguales. Así

Para evaluar esta expresión para valores grandes de N como 365 se requiere algo de valentía o, mejor aún, algunas buenas tablas de logaritmos. T. C. Fry en Probabilidad y sus usos en ingeniería, D. Van Nostrand Company, Inc., Princeton, New Jersey, 1928, proporciona tablas de logaritmos de factoriales, por lo que es conveniente evaluar la probabilidad de no tener cumpleaños iguales en la forma

Los siguientes datos ayudan:

Un breve encuentro con tablas de logaritmos muestra que para r = 23 la probabilidad de al menos un éxito es 0.5073, pero para r = 22 la probabilidad es 0.4757.

Por lo tanto, r = 23 es el número mínimo que da un50-50 de probabilidad de obtener algunos cumpleaños iguales.

La mayoría de las personas se sorprenden de que el número requerido sea tan pequeño, ya que esperaban alrededor de 365/2. Discutiremos esa noción en nuestro próximo problema, pero hagamos algo más con el actual.

Primero, la tabla da probabilidades de al menos un par de cumpleaños iguales para varios valores de r:

Segundo, aprendamos una forma complicada de aproximar la probabilidad de fracaso. Recuerde que

Si x fuera muy pequeño, entonces los términos más allá de 1 - x no serían significativos .

Consecuentemente, para valores pequeños de x podríamos aproximar e^-x por 1-x

Observa que N ( N - 1 ) ···(N-r + 1 ) / N^r

es un producto de r factores (N-k) / N  donde k es mucho menor que N,

Estos factores pueden escribirse como 1-k/N donde 0 ≤ k ≤ r

Por tanto

Para ver la aproximación en acción, pruébala en = 23 y obtén aproximadamente 0.500 . en lugar de 0.507. O establece

r ( r - 1 ) / 2 ( 365 )= -log.0.5 ≈ 0.693

y resuelve para r

Tercero, supongamos que el problema original se extendió para que quisieras el menor número para lograr al menos un par de cumpleaños idénticos o cumpleaños adyacentes (el 31 de diciembre es adyacente al 1 de enero).

Intenta este problema por tu cuenta.