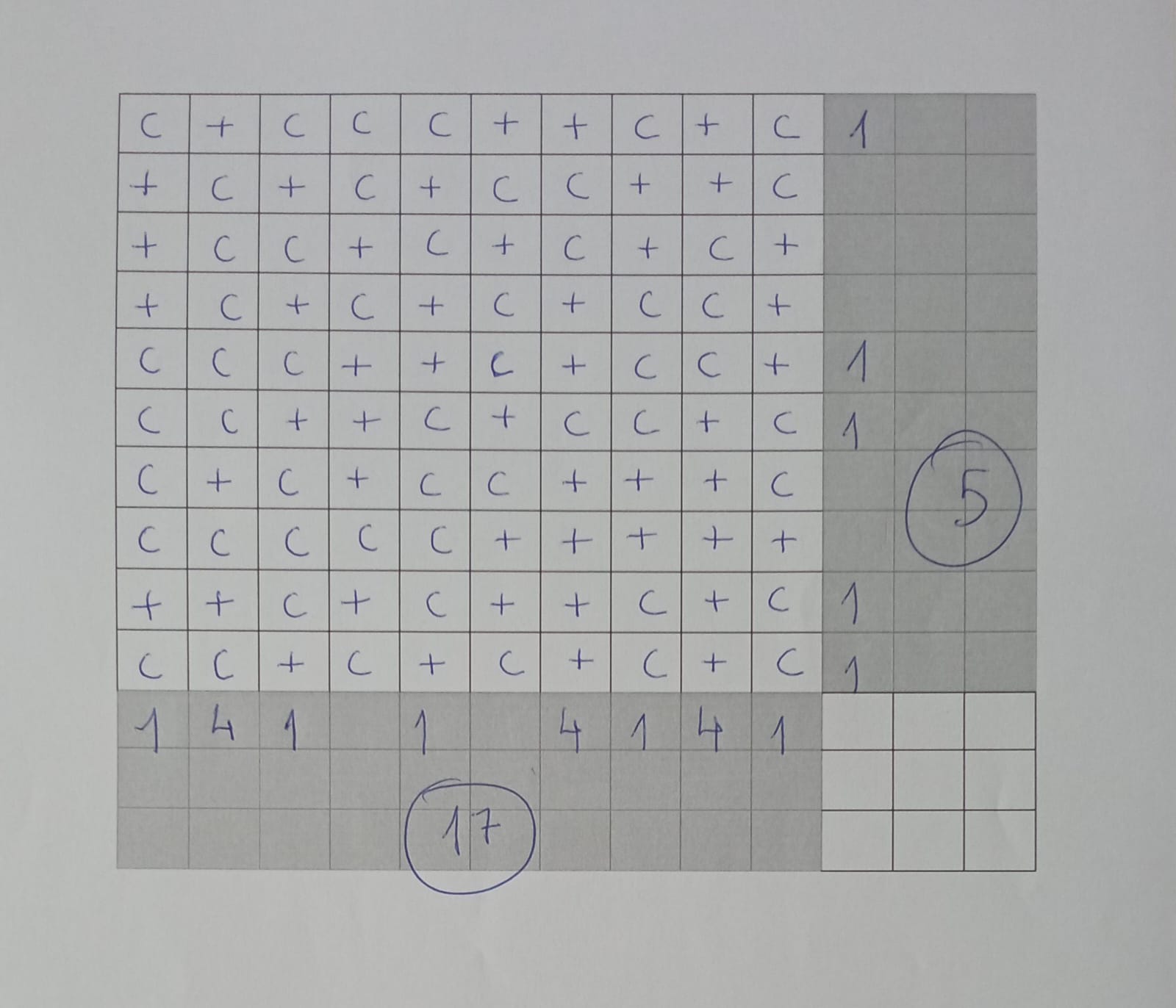
Experimento: Azar Humano vs. MáquinaEste estudio pone su enfoque en comparar los resultados de un experimento de azar realizado por humanos con aquellos generados por una máquina. La premisa es simple: ¿cuál es la diferencia entre el azar humano y el azar generado por una máquina? La Provocación del Experimento Con motivo del Día Internacional de las Matemáticas de 2024 (14 de marzo), la Real Academia de Ciencias Exactas en España organizó una serie de conferencias. La primera, impartida por el Dr. Juan Antonio Cuesta Albertos, Catedrático de Estadística de la UC, está disponible para su visualización completa aquí. A continuación, se presenta un resumen de nuestra actividad. A partir de estas conferencias, se recogieron 45 cuadrículas realizadas manualmente, siguiendo las indicaciones del profesor. Las cuadrículas recogidas tenían dimensiones de 10x10, con el propósito de estudiar la diferencia entre las sumas horizontales y verticales, destacando que los participantes no pensaron en la construcción vertical, sino en el rellenado horizontal. Se calculó el promedio de las relaciones SV/SH y SH/SV, así como sus cocientes respectivos. El Azar humano Una cuadrícula fue rellenada a mano por horizontales.
En la imagen, 5 es SH y 17 es SV , calculamos también SH/SV y SV/SH
¿Por qué 45 experimentos o hojas? Simplemente porque fueron los que se
recogieron en un día.
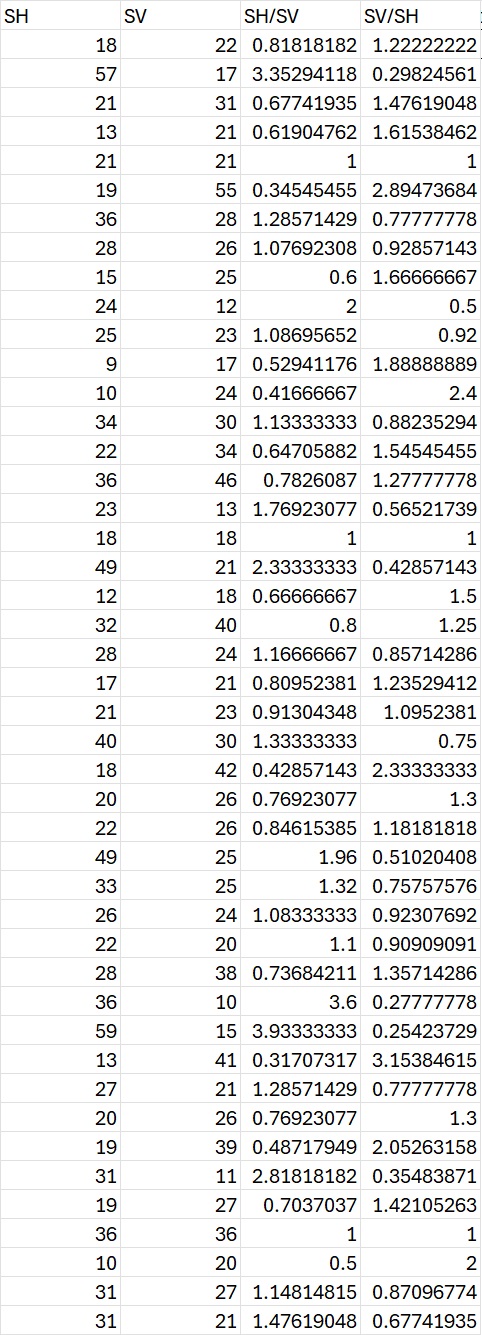
El experimento con java script Se llevó a cabo utilizando la ayuda del chatGPT. Una cuadrícula fue generada por horizontales con java script
Esta es la página con la que se generaron dferentes tarjetas, 100, cuyos resultados se muestran a continuación.
Copiamos de nuevo los promedios obtenidos con las cuadrículas a mano
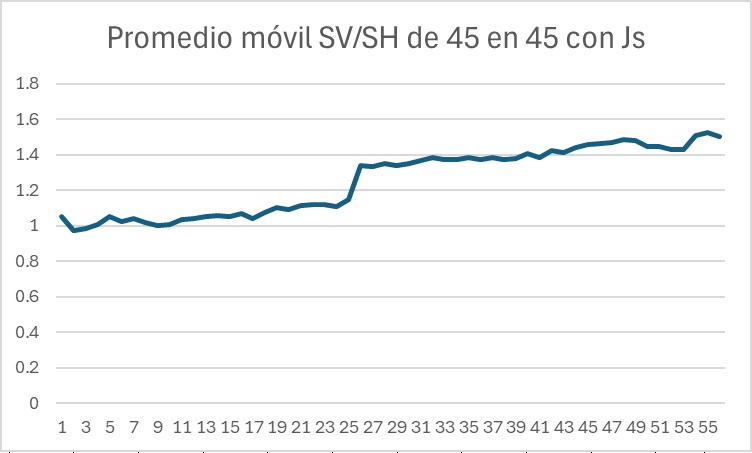
Llama la atención que en el experimento humano el promedio de los cocientes SV/SH, 2.49841167, es más del doble que el promedio de los cocientes SH/SV y sin embargo en el experimento con js son prácticamente iguales. Hemos calculado la tabla de los promedios móviles de SV/SH de 45 en 45 tarjetas
este es el gráfico
El experimento con excell
Simulamos el experimento con una hoja de calculo, de la misma forma, y
se completaron 45 hojas Los resultados con excell fueron
Y los promedios de SV/SH y SH/SV fueron respectivamente 1.18769783 1.18641166 Como en el experimento con javascript practicamente iguales. Con excell se volvio a completar 45 tarjetas 20 veces y los promedios obtenidos fueron
Y el promedio de estos promedios excell da 1.23985331 1.19543366 Con excell se han realizado 20 experimentos cada uno de 45 tarjetas y los promedios de SV/SH fueron siempre menores de 1.44. En el experimento a mano ese promedio fue mayor de 2.49.
Conclusiones En resumen, los experimentos realizados con Excel o JavaScript arrojaron un promedio aproximado de 1.2 para SV/SH, mientras que el promedio obtenido manualmente fue de alrededor de 2.5.
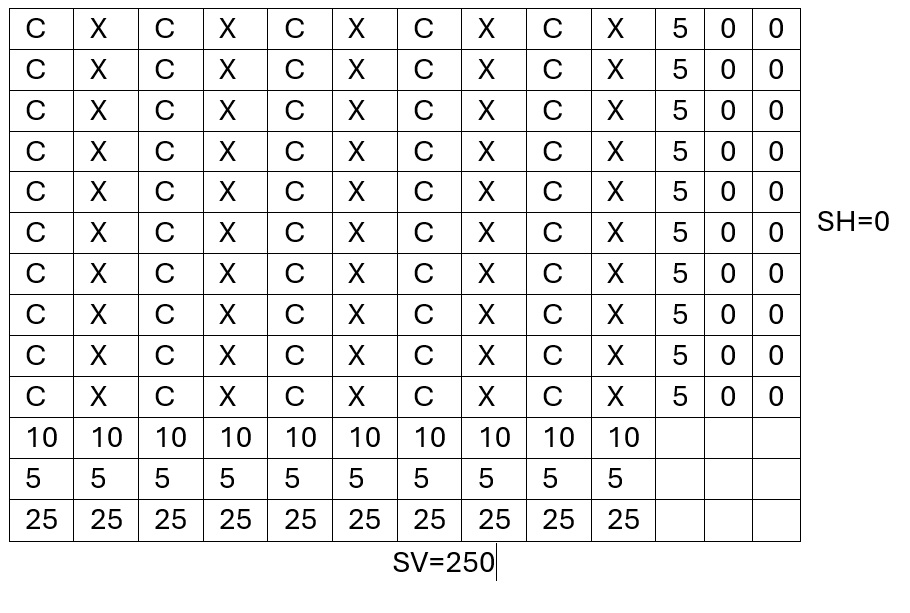
Máximo y mínimo de SV/SH Cuadrícula par En la cuadrícula 10x10 el valor máximo de SV es 250 y entonces SH es 0 con lo que el cociente sale 250/0
Para una cuadrícula 8x8 el máximo SV es 16·8 y SH en ese caso es 0, de modo que para n par el maximo SV es (n/2)2·n y SV/SH en este caso es (n/2)2·n/0 Para evitar este denominador 0 se podrían coger cuadrículas nxn con n impar
Cuadrícula impar
SV/SH en este caso es n2 Curioso este resultado: Cuando la cuadrícula nxn con n impar, el valor máximo para SV/SH es n2
Herramientas creadas con motivo de
este artículo Con ayuda de Chat GPT
Hoja de cálculo para generar 45 tarjetas diferentes cada vez.
Agradecimientos Queremos agradecer a todas las personas que colaboraron rellenando las 45 tarjetas con el formato de 10x10, sin cuya ayuda este experimento no habría sido posible. También agradecemos al Dr. Cuesta Albertos por inspirar esta idea con su conferencia y por estar siempre disponible para responder nuestras preguntas, así como al Catedrático D. Miguel Ángel Maestro Agustín por sus valiosas sugerencias.
Consolación Ruiz Gil Marzo 2024 https://www.matsolin.com/cx/index.htm
|