Traducción pp 318-335 de Mosteller

"Probability with Statistical Applications" (PWSA)

Obtenido en https://archive.org/details/probabilitywiths0000most/page/334/mode/1up?view=theater

9-2 La varianza de la distribución de la suma de dos variables aleatorias independientes

Para derivar la varianza de la suma de dos variables aleatorias independientes, definimos

$ U = X + Y $

donde $ X $ e $ Y $ son variables independientes, y $\mu_X, \mu_Y, \sigma_X^2, \sigma_Y^2$ son sus respectivas medias y varianzas. La ecuación (1) define una nueva variable aleatoria $ U $ cuya varianza, como la de cualquier variable aleatoria, es la media de su cuadrado menos el cuadrado de su media:

\[ \sigma_U^2 = E(U^2) - (E(U))^2 \]

Por lo tanto, sustituyendo desde la ecuación (1),

\[ \sigma_U^2 = E((X + Y)^2) - (\mu_X + \mu_Y)^2 \]

Sabemos por el Teorema 6-4 que:

\[ E((X + Y)^2) = E(X^2) + 2E(XY) + E(Y^2) \]

El término del medio de la última línea de la Ecuación (6) se deduce de la propiedad de que la media de un término constante multiplicado por una variable aleatoria es ese término constante multiplicado por la media:

\[ E(cY) = cE(Y) \]

Hasta ahora, no hemos usado la suposición de que $ X $ e $ Y $ son independientes. Ahora utilizamos su independencia y el Teorema 6-6, para escribir

\[ E(XY) = E(X)E(Y) = \mu_X \mu_Y \]

Ahora sustituimos desde la ecuación (7) en la ecuación (6), luego desde la ecuación (6) a la ecuación (3), y el resultado, junto con la ecuación (4), en la ecuación (2), para obtener

\[ \sigma_U^2 = E(X^2) + 2\mu_X\mu_Y + E(Y^2) - \mu_X^2 - 2\mu_X\mu_Y - \mu_Y^2 \]

\[ = \sigma_X^2 + \sigma_Y^2 \]

Por lo tanto, hemos establecido el siguiente teorema:

Teorema 9-1

$\sigma_U^2$ para variables independientes. Si $ U = X + Y $ y $ X, Y, U $ tienen varianzas $\sigma_X^2, \sigma_Y^2, \sigma_U^2$ y $ X $ e $ Y $ son independientes, entonces

\[ \sigma_U^2 = \sigma_X^2 + \sigma_Y^2 \]

Ejemplo 1

Una máquina fabrica pequeños discos redondos de un grosor de 0.5 pulgadas, pero con una desviación estándar del grosor de 0.003 pulgadas. Ensamblajes de dos discos uno encima del otro (como una pila en un juego de damas). ¿Cuál es la desviación estándar de las alturas de los ensamblajes de dos discos?

Solución. Deja que $ X $ sea el grosor del disco inferior y $ Y $ el grosor del superior, y $ U = (X + Y) $ para el grosor del ensamblaje. Suponemos que $ X $ e $ Y $ son independientes. Entonces

\[ \sigma_U^2 = (0.003)^2 + (0.003)^2 = (0.003)^2 (2) \]

\[ \sigma_U = 0.0042 \]

Ejemplo 2

Mediciones. Un niño corta tablas en longitudes de aproximadamente 3 pies, y la desviación estándar de las longitudes es de 0.2 pulgadas. Para comprobar su precisión, el niño mide las longitudes de las tablas y obtiene una distribución de mediciones con una desviación estándar de 0.25 pulgadas. ¿Cuál es la desviación estándar de su error de medición?

Solución. Deja que la variable aleatoria $ X $ represente la longitud real de una tabla, y deja que $ Y $ sea el error de medición; entonces la medición $ U = X + Y $. Supongamos que $ X $ e $ Y $ son independientes. Entonces $\sigma_X = 0.2$, $\sigma_U = 0.25$. Para encontrar $\sigma_Y$, sustituimos en

\[ \sigma_U^2 = \sigma_X^2 + \sigma_Y^2 \]

y obtenemos

\[ 0.0625 = 0.04 + \sigma_Y^2 \]

Resolviendo para $\sigma_Y^2$ obtenemos

\[ \sigma_Y^2 = 0.0225, \quad \sigma_Y = 0.15 \]

Por lo tanto, la desviación estándar de la distribución de los errores de medición es de 0.15 pulgadas, o aproximadamente el tamaño de la desviación estándar de la distribución de las longitudes reales. La medición del niño es casi tan precisa como su corte.

Ejemplo 3

Desviaciones estándar dispares. Deja que $ X $ tenga una desviación estándar $\sigma$ y $ Y $ una desviación estándar $ k\sigma $, donde $ k $ es grande comparado con 1. Encuentra aproximadamente la desviación estándar de $ U = X + Y $.

Solución. Por la fórmula (8),

\[ \sigma_U^2 = \sigma_X^2 + \sigma_Y^2 = \sigma^2 + (k\sigma)^2 = (k^2 + 1)\sigma^2 \]

\[ \sigma_U = \sqrt{(k^2 + 1)\sigma^2} = \sigma \sqrt{k^2 + 1} \approx k\sigma \]

Roughly, then, $\sigma_U \approx k\sigma = \sigma_Y$, la desviación estándar más grande.

Observación. La moraleja del Ejemplo 3 es que si una situación experimental involucra la suma de variables aleatorias, cuando sus varianzas deben añadirse, la reducción de una varianza grande cuenta mucho, pero la reducción de una pequeña variabilidad es casi inútil para reducir la variabilidad de la suma.

Uso de tablas normales. Cuando los datos son casi distribuidos normalmente y conocemos su media y varianza, podemos usar tablas normales (Tabla III) para calcular las probabilidades aproximadas.

Ejemplo 4. El desempeño en una prueba de álgebra y en una prueba de habilidades dramáticas son aproximadamente independientes, y la distribución de la suma de sus puntuaciones es aproximadamente normal. Si la distribución de las puntuaciones del examen tiene una media de 50 y una desviación estándar de 10, ¿qué proporción de examinados obtuvo una puntuación total de 125 puntos o más?

Solución. Deja que $ X $ sea la puntuación de álgebra, $ Y $ la puntuación dramática, $ U $ su total. Entonces

\[ \mu_U = 50 + 50 = 100, \quad \sigma_U^2 = 10^2 + 10^2 = 200, \quad \sigma_U = \sqrt{200} = 14.1 \]

Si dejamos

\[ Z = \frac{U - 100}{\sqrt{200}} \]

entonces $ Z $ es aproximadamente normal y tiene una media de 0 y una desviación estándar de 1. Podemos encontrar $ P(Z \geq a) $, aproximadamente, en la tabla normal, Tabla III. El evento $ U \geq 125 $ es equivalente al evento

\[ Z \geq \frac{125 - 100}{\sqrt{200}} \approx 1.77 \]

Por lo tanto,

\[ P(U \geq 125) \approx P(Z \geq 1.77) \]

y, de la Tabla III, encontramos

\[ P(Z \geq 1.77) \approx 0.0384 \]

Por lo tanto, aproximadamente el 4% de los examinados obtuvieron una puntuación de 125 o más.

Teorema 9-2. Sumas ponderadas de mediciones. Deja que las mediciones $ X $ e $ Y $ sean tomadas independientemente de distribuciones con medias $\mu_X, \mu_Y$ y varianzas $\sigma_X^2, \sigma_Y^2$. Deja que su suma ponderada, con pesos $ a $ y $ b $, sea una nueva variable aleatoria $ Z $:

\[ Z = aX + bY \]

Entonces

\[ \mu_Z = a\mu_X + b\mu_Y \]

\[ \sigma_Z^2 = a^2\sigma_X^2 + b^2\sigma_Y^2 \]

Prueba. Se le pide que demuestre este teorema en el Ejercicio 16.

Ejemplo 5. Precios de aleaciones. Los bloques fabricados de aleaciones costosas se venden por peso. Los bloques de la aleación A tienen una desviación estándar de 3 libras y cuestan $100 por libra. Los bloques de la aleación B tienen una desviación estándar de 4 libras y cuestan $50 por libra. En pedidos repetidos de dos bloques (uno de A y uno de B), ¿cuál es la desviación estándar del precio total si los bloques se ensamblan independientemente para completar el pedido?

Solución. Sea $ X $ el peso en libras de un bloque de la aleación A, $ Y $ el de la aleación B. Entonces, el precio total en dólares es

\[ Z = 100X + 50Y \]

Por el Teorema 9-2,

\[ \sigma_Z^2 = 100^2\sigma_X^2 + 50^2\sigma_Y^2 = 130,000 \]

\[ \sigma_Z = \sqrt{130,000} = 361 \, \text{dólares} \]

Corolario 9-3. Diferencias. Si $ X $ e $ Y $ son independientes, con medias $\mu_X, \mu_Y$ y varianzas $\sigma_X^2, \sigma_Y^2$, entonces la distribución de su diferencia $ D $,

\[ D = X - Y \]

tiene media

\[ \mu_D = \mu_X - \mu_Y \]

y varianza

\[ \sigma_D^2 = \sigma_X^2 + \sigma_Y^2 \]

Prueba. El Teorema 9-2 se aplica a este corolario cuando tomamos $ a = 1, b = -1, a^2 = 1, b^2 = 1 $. Sustituyendo estos valores en las Ecuaciones (10) y (11) obtenemos las Ecuaciones (13) y (14).

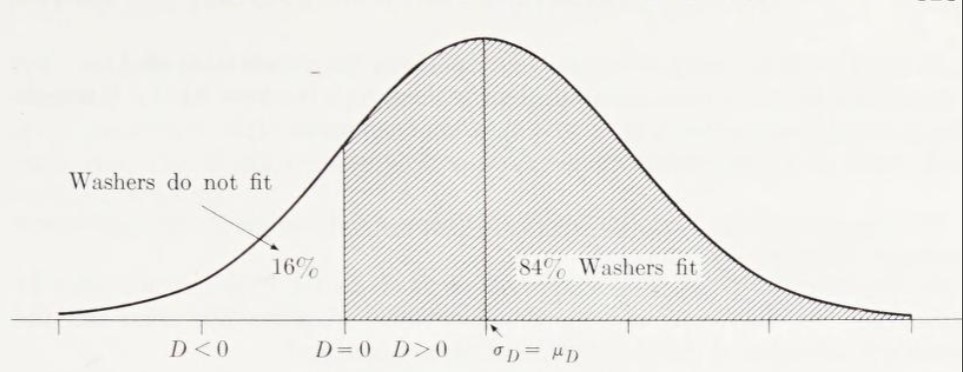
Ejemplo 6. Varillas con arandelas. Las varillas (circulares en sección transversal) tienen diámetros externos que se distribuyen normalmente con una media de 1.000 pulgadas y una desviación estándar de 0.003 pulgadas. Las arandelas (con orificios circulares en sección transversal) tienen diámetros internos que se distribuyen normalmente con una media de 1.005 pulgadas y una desviación estándar de 0.004 pulgadas. Cuando las varillas y las arandelas se emparejan aleatoriamente, ¿qué proporción de las arandelas son demasiado pequeñas para caber en sus varillas? (Suponga que la diferencia de dos variables independientes distribuidas normalmente también se distribuye normalmente).

Solución. Deja que $ X $ mida el diámetro interno de una arandela en pulgadas, $ Y $ el diámetro externo de una varilla. Entonces deja que $ D = X - Y $ mida la diferencia en estos diámetros. Si $ D > 0 $, la varilla cabe en el orificio, de lo contrario, no.

Por el Corolario 9-3,

\[ \mu_D = 1.005 - 1.000 = 0.005 \, \text{pulgadas}, \]

\[ \sigma_D^2 = 0.004^2 + 0.003^2 = 0.000016 + 0.000009 = 0.000025 \, \text{pulgadas}^2 \]

\[ \sigma_D = \sqrt{0.000025} = 0.005 \, \text{pulgadas}. \]

Dado que $ \mu_D = \sigma_D $, el porcentaje de arandelas demasiado pequeñas para caber en sus varillas es igual a la probabilidad a la izquierda de -1 para una variable aleatoria normal estándar $ Z $, donde

\[ Z = \frac{D - \mu_D}{\sigma_D}. \]

Si $ D < 0 $, entonces $ Z < -1 $, y

Probabilidad (la arandela no cabe) = $ P(D < 0) = P(Z < -1) $.

De la Tabla III,

\[ P(Z < -1) = P(Z > 1) = 0.5000 - P(0 \leq Z \leq 1) = 0.1587. \]

Por lo tanto, aproximadamente el 16% de las arandelas son demasiado pequeñas para caber en sus varillas (Fig. 9-1).

Figura 9-1: Distribución de la diferencia de diámetros de varillas y arandelas.

Ejercicios para la sección 9-2

En los ejercicios 1 a 5, $ X $ e $ Y $ son independientes, $ U = X + Y $.

Las variables $ X $ y $ Y $ toman ambos valores -1, 0, 1 con probabilidades iguales de $ \frac{1}{3} $. Encuentra $ \sigma_U^2 $.
Encuentra los valores faltantes en la siguiente tabla:

	$\sigma_X$	$\sigma_Y$	$\sigma_U$
(a)	3	4	25
(b)	7		25
(c)	9	40
(d)		8	10
(e)	8		17
(f)		12	13
(g)	1	1	2
(h)	1	1

3. Si $\sigma_U^2 = 8$, $\sigma_Y^2 = 8$, ¿qué puedes decir sobre la distribución de $X$?

4. ¿Qué teorema de la geometría plana se parece a la Ecuación (8)? ¿A qué corresponden $\sigma_X$, $\sigma_Y$ y $\sigma_U$ en ese teorema de geometría?

5. Si $\sigma_X = \sigma_Y$, muestra que $\sigma_U = \sqrt{2}\sigma_X$. (¿Por qué no $-\sqrt{2}\sigma_X$?)

6. (Continuación.) Usa el resultado del Ejercicio 5 para resolver el problema del ensamblaje de discos, Ejemplo 1 del texto.

7. Cuando se lanza un dado, un hombre recibe $4 si aparece un uno, pero pierde $1 de lo contrario. Sobre esta base, si un dado se lanza dos veces, ¿cuál es la media y la desviación estándar de la distribución de sus ingresos netos?

8. (Continuación.) Supón que en el juego del Ejercicio 7 el dado se lanza una tercera vez. ¿Cuál es la media y la desviación estándar de la distribución de sus ingresos netos en las tres tiradas? (Pista. Deja que el resultado de las dos primeras tiradas sea $X_1$.)

9. Las puntuaciones de los exámenes del College Board tienen una media de 500 y una desviación estándar de 100. Si se seleccionan dos estudiantes al azar de los examinados del College Board, aproximadamente, ¿cuál es la media y la desviación estándar de la distribución de la suma de sus puntuaciones en matemáticas?

10. (Continuación.) Considera que los exámenes del College Board incluyen tanto inglés como matemáticas. Encuentra la media y la desviación estándar de la distribución de la suma de las dos puntuaciones, o explica por qué no puedes.

11. En una gran operación química, un hombre saca material con dos cucharas, una con capacidad de una libra y la otra de dos libras. Para un trabajo preciso, usa la cuchara de una libra dos veces para poner dos libras de material en la mezcla. La desviación estándar de la distribución del peso de la cuchara de dos libras es de 0.5 onzas, para una cuchara de una libra es de 0.3 onzas. ¿Debería haber usado la cuchara de dos libras para mayor precisión?

12. Se dan dos pruebas con puntuaciones independientes $X$ y $Y$. Tienen desviaciones estándar de 7 y 24. Para cada estudiante tomamos la suma de sus puntuaciones en las pruebas, $X + Y$. Muestra que la desviación estándar de la distribución de estas puntuaciones $X + Y$ es 25.

13. Las distribuciones de longitudes de dos tipos de partes de madera $A$ y $B$ son aproximadamente normales, con medias $\mu_A = 2$ pulgadas y $\mu_B = 4$ pulgadas, y desviaciones estándar $\sigma_A = 0.009$ pulgada, $\sigma_B = 0.040$ pulgada. Una parte $A$ y una parte $B$ se ensamblan al azar y se colocan de extremo a extremo para formar una longitud de aproximadamente 6 pulgadas. Si un ensamblaje debe encajar, debe estar entre 5.92 y 6.08 pulgadas de largo. ¿Qué porcentaje de ensamblajes aleatorios no encajan? (Supón que la distribución de la suma de dos variables aleatorias independientes distribuidas normalmente es normal).

14. Dos mediciones $X$ y $Y$ se extraen de la misma distribución con media $\mu$ y varianza $\sigma^2$, y se calcula una suma ponderada $S = wX + (1 - w)Y$. (a) Encuentra $\mu_S$. (b) Encuentra $\sigma_S^2$. (c) Encuentra el valor de $w$ que minimiza $\sigma_S^2$. (d) Encuentra el valor mínimo de $\sigma_S^2$. [Observación. Para cualquier $w$, $S$ se llama una estimación imparcial de $\mu$ porque $\mu_S = \mu$, y con $w = \frac{1}{2}$, $S$ se llama la estimación de varianza mínima imparcial de $\mu$.]

15. Un ensamblaje se realiza poniendo dos objetos similares a arandelas cara a cara en un eje. Si el grosor total de los dos objetos está entre 0.549 y 0.551 pulgadas inclusivas, el ensamblaje es satisfactorio; de lo contrario, no lo es. Los objetos se ensamblan aleatoriamente de una población con un grosor medio de 0.275 y una desviación estándar de 0.0006 pulgadas. ¿Qué porcentaje de los ensamblajes es insatisfactorio? (Supón que la distribución de la suma de dos variables aleatorias normales independientes es normal).

16. Demuestra el Teorema 9-2 (relacionado con sumas ponderadas de mediciones).

En los Ejercicios 17 a 19, $X, Y, Z$ son variables aleatorias independientes que toman los siguientes valores, cada uno con una probabilidad de $\frac{1}{4}$:

Valores de $X$:	-4, -1, 2, 3
Valores de $Y$:	-3, -1, 2, 3
Valores de $Z$:	-2, -1, 0, 3

17. Calcula $\sigma_{X+Z}^2$ por definición y por fórmula.

18. Calcula $\sigma_{X+Y}^2$ por definición y por fórmula.

19. Calcula $\sigma_{3X+Z-4Y}^2$ por definición y por fórmula.

9-3. VARIANZA DE LA SUMA Y DEL PROMEDIO DE VARIAS VARIABLES

Para resolver el problema de la distribución de promedios de muestras para el problema de 100 dados dado al principio de este capítulo, necesitamos primero la varianza de la suma de muchas variables independientes, no solo dos, como tratamos en la Sección 9-2. A medida que tengamos la varianza de la suma, obtenemos la varianza de promedios de muestras por una operación trivial.

Subíndices para variables aleatorias. Nota que previamente hemos usado subíndices principalmente en los valores de las variables aleatorias, tales como $X_1$, no en las variables aleatorias mismas, porque solo había unas pocas de ellas. Ahora estudiamos muchas variables aleatorias, por lo que necesitamos subíndices para ellas. Este es un teorema sobre la suma de $n$ variables aleatorias, por lo que denotamos las variables aleatorias por $X_1, X_2, \ldots, X_n$. Pero si solo tenemos unas pocas variables aleatorias, continuamos denotándolas por $X, Y, Z$.

Para extender el teorema sobre la varianza de la suma de dos variables aleatorias, necesitamos mostrar que podemos agregar una variable más, y luego otra, y así sucesivamente. Por ejemplo, si $X, Y$ y $Z$ son tres variables aleatorias independientes, sabemos que la varianza de $U = X + Y$ es $\sigma_U^2 = \sigma_X^2 + \sigma_Y^2$. Si $Z$ es independiente de $X$ y de $Y$, naturalmente esperamos que sea independiente de su suma $U$. Si $Z$ es independiente de $U$, entonces sabemos que $W = U + Z$ tiene varianza $\sigma_W^2 = \sigma_U^2 + \sigma_Z^2 = \sigma_X^2 + \sigma_Y^2 + \sigma_Z^2$. Dado que $Z$ es independiente de $U$, este argumento es suficiente para mostrar que tenemos un método general para agregar una variable más. Por lo tanto, podemos extender el teorema de 3 variables aleatorias independientes a 4, luego de 4 a 5, y así sucesivamente a $n$ variables. Por supuesto, un desarrollo riguroso requiere un argumento de inducción más formal.

Todo el argumento anterior depende del hecho intuitivamente obvio pero algo sutil de que si $X$, $Y$ y $Z$ son conjuntamente independientes, entonces las dos variables $Z$ y $U ( = X + Y)$ son independientes. La declaración es cierta, pero su prueba, aunque fácil, requiere una notación adicional que no hemos desarrollado. Se da una prueba en el Apéndice III. Esta prueba junto con los argumentos anteriores completa la demostración del siguiente teorema deseado:

Teorema 9-4. Varianza de sumas de variables aleatorias independientes.

Si $X_1, X_2, \ldots, X_n$ son variables aleatorias independientes con varianzas $\sigma_1^2, \sigma_2^2, \ldots, \sigma_n^2$, y

\[ T = X_1 + X_2 + \cdots + X_n, \]

entonces

\[ \sigma_T^2 = \sigma_1^2 + \sigma_2^2 + \cdots + \sigma_n^2. \]

Ejemplo 1. Ensamblaje de tres unidades.

En un circuito eléctrico, las resistencias en serie forman una resistencia igual a la suma de sus resistencias. Una resistencia de 10,000 ohmios, una de 20,000 ohmios y una de 50,000 ohmios se extraen cada una de un gran stock para formar una resistencia de 80,000 ohmios. Las desviaciones estándar de estos tres tipos son 30, 60 y 150 ohmios, en ese orden. Encuentra la desviación estándar de la distribución de las resistencias de 80,000 ohmios formadas de esta manera.

Solución. Si las resistencias se ensamblan al azar, entonces

\[ \sigma^2 = (30)^2 + (60)^2 + (150)^2 = 27,000, \] \[ \sigma = \sqrt{27,000} \approx 164. \]

Nota. Se dice que dos o más variables aleatorias están idénticamente distribuidas si sus funciones de probabilidad son iguales.

Corolario 9-5. Varianza de variables idénticamente distribuidas: teoría del muestreo.

Si $X_1, X_2, \ldots, X_n$ son variables aleatorias independientes e idénticamente distribuidas con medias $\mu$ y varianzas $\sigma^2$, y si

\[ T = X_1 + X_2 + \cdots + X_n, \]

entonces

\[ \mu_T = n\mu, \]

\[ \sigma_T^2 = n\sigma^2. \]

Prueba. La Ecuación (2) se deduce de inmediato del Corolario 6-5, Sección 6-1. La Ecuación (3) se obtiene sustituyendo $\sigma^2$ por cada $\sigma_i^2$ en la Ecuación (1) del Teorema 9-4 anterior.

En los Capítulos 7 y 8 usamos frecuentemente el hecho de que la varianza de la distribución binomial es

\[ \sigma^2 = npq = np(1 - p). \]

Ahora proporcionamos la tan esperada prueba.

Corolario 9-6. Varianza de una distribución binomial.

Sea $p$ la probabilidad de éxito en una sola prueba binomial, y sea $X$ el número total de éxitos en $n$ tales pruebas. Entonces la varianza de $X$ es

\[ \sigma_X^2 = np(1 - p). \]

Prueba.

La distribución del número de éxitos, $B$, en una prueba binomial es

Probabilidad	p	1 - p
Número de éxitos	1	0

Por consiguiente, el número medio de éxitos en una sola prueba es

\[ \mu_B = p \cdot 1 + (1 - p) \cdot 0 = p. \]

La varianza del número de éxitos en una sola prueba es

\[ \sigma_B^2 = E(B^2) - \mu_B^2 = 1^2p + 0^2(1 - p) - p^2 = p - p^2 = p(1 - p). \]

El número total de éxitos en $n$ pruebas es la suma de $n$ variables aleatorias independientes como $B$, una para cada prueba, y cada una con media $p$ y varianza $p(1 - p)$. Por lo tanto, la media, la varianza y la desviación estándar para el número de éxitos en $n$ pruebas se dan por las fórmulas:

(a) $\mu_X = np$, (b) $\sigma_X^2 = np(1 - p)$, (c) $\sigma_X = \sqrt{np(1 - p)}$. \quad (5)

Ejemplo 2. 1000 chinchetas. Si las chinchetas tienen una probabilidad $p = 0.3$ de caer con la punta hacia arriba, ¿cuál es la probabilidad de que al menos 320 de 1000 chinchetas lanzadas caigan con la punta hacia arriba?

Solución. Sea $X$ el número de chinchetas que caen con la punta hacia arriba. Entonces, por la Ecuación (5), la media de $X$ es $(0.3)(1000) \approx 300$, y la desviación estándar es $\sigma_X = \sqrt{1000(0.3)(0.7)} \approx 14.5$. Así, si 320 caen con la punta hacia arriba, el número de "éxitos" en exceso de la media es $320 - 300 = 20$, y el número de desviaciones estándar de la media es $20 / 14.5 \approx 1.38$. De la Tabla III, la probabilidad de un exceso de 1.38 desviaciones estándar es aproximadamente 0.0838, o alrededor del 8%.

Teorema del límite central.

En el Capítulo 7 estudiamos el comportamiento de la distribución binomial a medida que $n$ aumenta. Encontramos que si $X$ es el número de éxitos en $n$ pruebas binomiales independientes, entonces la variable aleatoria relacionada

\[ Z = \frac{X - np}{\sqrt{npq}} \]

tiene una distribución que se aproxima estrechamente a la distribución normal estándar si $n$ es grande. Ese resultado es un caso especial de un teorema más general llamado teorema del límite central, que ahora enunciamos y usamos, sin prueba.

Teorema 9-7. Teorema del límite central.

Sean $X_1, X_2, \ldots, X_n, \ldots$ una secuencia de variables aleatorias independientes idénticamente distribuidas, cada una con media $\mu$ y varianza $\sigma^2$. Sea

\[ T_n = X_1 + X_2 + \cdots + X_n. \]

Entonces, para cada valor fijo de $z$, a medida que $n$ tiende al infinito,

\[ P\left( \frac{T_n - n\mu}{\sigma \sqrt{n}} > z \right) \]

se aproxima a la probabilidad de que la variable aleatoria normal estándar $Z$ exceda $z$.

Observación. Restando $E(T_n) = n\mu$ de $T_n$ y luego dividiendo por $\sigma \sqrt{n} = \sqrt{n\sigma^2} = \sqrt{\text{Var}(T_n)}$, obtenemos una nueva variable aleatoria cuya media es cero y cuya desviación estándar es 1, como las de la normal estándar. En trabajos más avanzados en probabilidad, se prueba que la distribución de esta nueva variable aleatoria se aproxima a la de la normal estándar a medida que $n$ tiende al infinito. En términos prácticos, esto significa que si $n$ es grande, podemos usar las tablas de la normal estándar para responder a preguntas como la del siguiente ejemplo.

Ejemplo 3. 100 dados. Encuentra la probabilidad de que cuando se lanzan 100 dados, la suma de los puntos en sus caras superiores exceda 325.

Solución. Para el lanzamiento de un dado, encontramos la media y la varianza del número de puntos en una cara en el Ejemplo 3, Sección 5-4, que son

\[ \mu = 3.5, \quad \sigma^2 = \frac{35}{12}. \]

Aplicando el Corolario 9-5 con $n = 100$, encontramos que la media, la varianza y la desviación estándar de la suma de 100 lanzamientos son

\[ \mu_T = 100(3.5) = 350, \] \[ \sigma_T^2 = 100 \left(\frac{35}{12}\right), \] \[ \sigma_T \approx 17.1. \]

Entonces, el valor 325 está a -25 de la media, o $\frac{25}{17.1} \approx 1.46$ desviaciones estándar a la izquierda de la media. Con la ayuda de la Tabla III, encontramos que la probabilidad a la derecha de -1.46 es 0.9279 para la normal estándar, o aproximadamente el 7%.

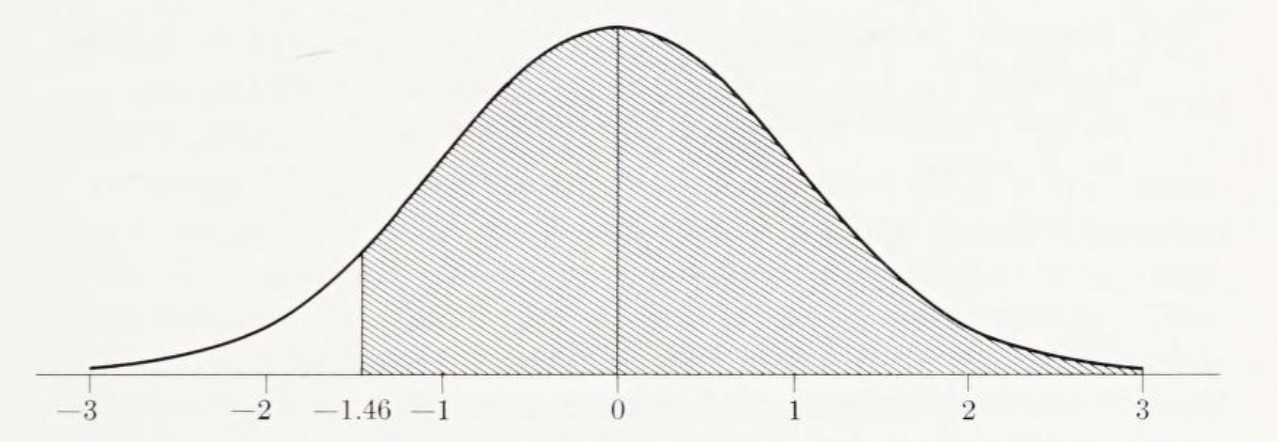
Figura 9-2: El área sombreada da la probabilidad de que la puntuación total en 100 dados exceda 325.

Pasando de sumas a promedios.

Si dividimos una suma por su número de mediciones, obtenemos un promedio. Por lo tanto, un promedio es un ajuste trivial de una suma. El Teorema 9-7 completa la información que necesitamos sobre la distribución de una suma. Ahora derivamos rápidamente la media y la varianza de la distribución de promedios muestrales. Estos resultados confirmarán la noción intuitiva de que los promedios muestrales son más estables que las mediciones individuales.

Como en el Teorema 9-4, sea

\[ T = X_1 + X_2 + \cdots + X_n. \]

Entonces, el promedio muestral es

\[ \bar{X} = \frac{T}{n}. \]

Sabemos que cuando multiplicamos una variable aleatoria por una constante, multiplicamos su media, o valor esperado, por esa misma constante y multiplicamos su varianza por el cuadrado de la constante. Por lo tanto,

\[ \mu_{\bar{X}} = \frac{1}{n} \mu_T, \quad \sigma_{\bar{X}}^2 = \frac{1}{n^2} \sigma_T^2. \]

Por supuesto, dado que la media de una suma es la suma de las medias,

\[ \mu_T = \mu_1 + \mu_2 + \cdots + \mu_n, \]

y por el Teorema 9-4,

\[ \sigma_T^2 = \sigma_1^2 + \sigma_2^2 + \cdots + \sigma_n^2. \]

Así, hemos demostrado el siguiente teorema.

Teorema 9-8. Medias y varianzas de promedios muestrales.

Sean las variables aleatorias $X_1, X_2, \ldots, X_n$ independientes, con medias $\mu_1, \mu_2, \ldots, \mu_n$ y varianzas $\sigma_1^2, \sigma_2^2, \ldots, \sigma_n^2$. Sea el promedio de estas variables $\bar{X}$, donde

\[ \bar{X} = \frac{1}{n} (X_1 + X_2 + \cdots + X_n). \]

Entonces $\bar{X}$ tiene una distribución con media

\[ \mu_{\bar{X}} = \frac{1}{n} (\mu_1 + \mu_2 + \cdots + \mu_n) \quad \text{(6)} \]

y varianza

\[ \sigma_{\bar{X}}^2 = \frac{1}{n^2} (\sigma_1^2 + \sigma_2^2 + \cdots + \sigma_n^2). \quad \text{(7)} \]

Corolario 9-9. Promedios de variables aleatorias independientes que tienen medias y varianzas idénticas.

Sean las variables independientes $X_1, X_2, \ldots, X_n$ con medias idénticas, $\mu$, y varianzas, $\sigma^2$, y sea su promedio

\[ \bar{X} = \frac{1}{n} (X_1 + X_2 + \cdots + X_n). \]

Entonces,

\[ \mu_{\bar{X}} = \mu \quad \text{(8)} \]

\[ \sigma_{\bar{X}}^2 = \frac{\sigma^2}{n}, \quad \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}}. \quad \text{(9)} \]

Prueba. Sustituye en las Ec. (6) y (7) del Teorema 9-8.

Muestreo con reemplazo.

La aplicación más importante del Corolario 9-9 es el muestreo con reemplazo de una población finita, o el muestreo de una población infinita. Sea $X_1$ una característica medida del elemento de la población que se extrae primero en la muestra, $X_2$ la del elemento que se extrae segundo, y así sucesivamente. En el muestreo con reemplazo, las funciones de probabilidad de las variables aleatorias $X_1, X_2, \ldots, X_n$ son las mismas; las variables son idénticamente distribuidas. Así, las mediciones observadas en tales muestras son valores de variables aleatorias con medias y varianzas iguales, por lo que se aplica el Corolario 9-9.

En palabras, las Ecuaciones (8) y (9) dicen que el valor esperado del promedio de $n$ mediciones es la media de la población $\mu$, y la desviación estándar de los promedios de un conjunto de mediciones a otro es inversamente proporcional a la raíz cuadrada del número de mediciones. Así, los promedios de 4 mediciones independientes extraídas de la misma población tienen una desviación estándar igual a $\frac{1}{2}$ la desviación estándar de mediciones individuales; y los promedios de 100 mediciones independientes extraídas de la misma población tienen una desviación estándar igual a $\frac{1}{10}$ la desviación estándar de mediciones individuales. Esta reducción de la desviación estándar a medida que $n$ aumenta causa un ajuste de la distribución de probabilidad de $X$ alrededor de la media de la población y prácticamente garantiza que el promedio muestral se sitúe cerca de la media de la población cuando $n$ es suficientemente grande.

Sesgo, o error sistemático.

En un procedimiento de medición real, puede haber un error sistemático. Por ejemplo, uno puede tender constantemente a leer demasiado alto. Tal error sistemático no se reduce al tomar el promedio de mediciones repetidas.

Ejemplo 4. Promedio para 100 dados.

Encuentra la probabilidad de que cuando se lanzan 100 dados, su promedio muestral exceda 3.7.

Solución. Para un solo dado, $\mu = 3.5, \sigma^2 = \frac{35}{12}$. Por el Corolario 9-9,

\[ \mu_{\bar{X}} = \mu = 3.5, \quad \sigma_{\bar{X}}^2 = \frac{\sigma^2}{n} = \frac{35}{12 \cdot 100} \approx 0.0292, \quad \text{y} \quad \sigma_{\bar{X}} \approx 0.171. \]

Si el promedio muestral excede 3.7, entonces excede la media de la población 3.5 en al menos 0.2 ($= 3.7 - 3.5$), o en $0.2 / 0.171 \approx 1.17$ desviaciones estándar. De las tablas de la normal, la probabilidad de un exceso de 1.17 desviaciones estándar es 0.121. Hay menos de una posibilidad en 8 de que el promedio muestral para los 100 dados exceda 3.7.

Corolario 9-10. Proporción media de éxitos para la binomial.

Considera un experimento binomial compuesto por $n$ ensayos binomiales, cada uno con una probabilidad $p$ de éxito y con un número total de éxitos $X$. Sea $\overline{p} = X / n$ la proporción de éxitos. Entonces, la media y la varianza de $\overline{p}$ son

\[ \mu_{\overline{p}} = p \quad \text{y} \quad \sigma_{\overline{p}}^2 = \frac{p(1 - p)}{n}. \quad \text{(10)} \]

Prueba. La prueba para la media se dio en la Sección 8-2; la varianza sigue del Corolario 9-6, ya que $\sigma_{\overline{p}}^2 = (1/n^2) \sigma_X^2$.

Ejemplo 5. Votación.

Si el 60% de una gran población apoya a cierto candidato, ¿cuál es la probabilidad de que en una muestra aleatoria de 100 votantes, la proporción a favor del candidato sea inferior al 50%?

Solución. $\mu_{\overline{p}} = p = 0.6, \sigma_{\overline{p}}^2 = \frac{(0.6)(0.4)}{100} = 0.0024, \sigma_{\overline{p}} \approx 0.049$. La diferencia $0.5 - 0.6 = -0.1$ es $-0.1 / 0.049 \approx -2$ desviaciones estándar, o 2 desviaciones estándar por debajo de la media. Usando la aproximación normal, encontramos que la probabilidad es aproximadamente 0.025, o alrededor de 1 oportunidad en 40.

Ejercicios para la Sección 9-3

En estos ejercicios, las muestras se extraen con reemplazo.

En los Ejercicios 1 a 10, la población tiene una media $\mu = 6$ y una desviación estándar $\sigma = 10$.

¿Cuál es la varianza?
¿Cuál es la desviación estándar de los promedios de muestras de tamaño 4 extraídas de esta población?
¿A qué desviación estándar, $x' = (x - \mu) / \sigma$, corresponde la observación 16?
Se forma una nueva población agregando 3 a cada observación en la población dada. Encuentra la media y la desviación estándar de la nueva población.
Se forma una nueva población multiplicando cada observación en la población dada por 3. Encuentra la media y la desviación estándar de esta nueva población.
Encuentra la media y la desviación estándar de la distribución formada tomando la suma de las observaciones de cada muestra de tamaño 4 extraída de la población original con reemplazo.

El Teorema de Chebyshev garantiza que al menos el 75% de la población original se encuentra entre ¿qué dos números?
Si la población original está distribuida normalmente, ¿qué proporción de ella se encuentra a la derecha de la media?
Si la población original está distribuida normalmente, ¿qué proporción de ella tiene valores mayores que 11?
Si la población original está distribuida normalmente, ¿cuál es el valor superado por el 80% de la población?
La desviación estándar de una población de puntuaciones es 36. ¿Cuál es la desviación estándar de la distribución de los promedios muestrales para muestras de tamaño 16 extraídas de esta población?
Una gran población de mediciones tiene una media $\mu = 20$ y una desviación estándar $\sigma = 5$. Considera muestras de 4 mediciones, cada una extraída al azar de la población original. ¿Cuál es el valor esperado del promedio muestral $\overline{X}$ para tales muestras? ¿Cuál es la desviación estándar de la distribución de $\overline{X}$?
La distribución de los pesos (en libras) de un gran grupo de reclutas equipados se aproxima muy bien a una curva normal con una media de 185.0 libras y una desviación estándar de 15.0 libras.
1. Si se eligen dos reclutas al azar de este grupo, ¿cuál es la probabilidad de que ambos pesen entre 170.0 y 200.0 libras?
2. Si 81 reclutas del grupo grande deben embarcar con una asignación de 190.0 libras por hombre, ¿cuál es la probabilidad de que el transporte esté sobrecargado?

Una prueba mental determinada produce puntuaciones en meses de edad mental. Los errores de medición en esta prueba promedian cero a largo plazo, con una desviación estándar $\sigma$ de 2 meses. Una clase de quinto grado de 36 estudiantes tomó esta prueba. ¿Cuál es la probabilidad de que la puntuación promedio de la clase esté en error por 1 mes o más (ya sea demasiado alta o demasiado baja)?
Dada una gran población de puntuaciones de prueba con media 20 y varianza 9. ¿Cuál es la desviación estándar de la distribución de muestreo de promedios de muestras de tamaño 25 extraídas de esta población?
Al cruzar dos flores rosas de una cierta variedad, las flores resultantes son blancas, rojas o rosas, y las probabilidades asociadas a estos diversos resultados son $\frac{1}{4}, \frac{1}{4}$ y $\frac{1}{2}$ respectivamente. Si se obtienen 300 flores al cruzar flores rosas de esta variedad, ¿cuál es la probabilidad de que 90 o más de estas flores sean blancas?
En una cierta sociedad grande, la desviación estándar del número de hijos en una familia es 1.5. Si un antropólogo quiere que la desviación estándar de $\overline{X}$, su estimación del número medio de hijos por familia, sea 0.1, ¿cuántas familias deben estar en su muestra aleatoria?
La desviación estándar de la distribución de promedios muestrales en muestras de tamaño 9 es 4. ¿Cuál es la desviación estándar de la población de la cual se extrae la muestra?
Un objeto producido en masa tiene 2 caras espejadas. Los porcentajes de tales objetos con 2, 1 o 0 caras espejadas dañadas son 1, 1, 98, respectivamente.
1. Si cuatro objetos se eligen al azar de un grupo muy grande con esta composición, calcula la probabilidad exacta de que 2 o menos caras dañadas sean todas sin daño (calcula como si el muestreo se realizara con reemplazo).
2. Si 900 objetos se eligen al azar de esta población, ¿cuál es la probabilidad de que al menos 10 objetos tengan ambas caras sin daño?

El tiempo de escucha por semana de los programas musicales de una estación de radio por un grupo grande de personas está aproximadamente distribuido normalmente, con una media $\mu = 4$ horas y una desviación estándar $\sigma = 1$ hora. Una muestra de 16 personas extraídas de este grupo tiene un tiempo promedio de escucha $\overline{X}$. ¿Cuál es la probabilidad de que $\overline{X}$ difiera de la media del grupo en más de media hora?
En un experimento antes y después, la diferencia media en la población es 1.00, y la desviación estándar de las diferencias para los individuos en la población es 2.00. Encuentra la probabilidad de una diferencia positiva para un individuo seleccionado al azar.

De una distribución con varianza $\sigma^2 = 1$, se extraen dos muestras independientes como en la siguiente tabla:

Tamaño de la muestra	Promedio de la muestra
Muestra 1	10	$\overline{X}_1$
Muestra 2	5	$\overline{X}_2$

Para estimar la media de la población:

Un hombre pondera los promedios de las muestras en proporción a sus tamaños de muestra y afirma que la varianza muestral de tal estimación ponderada, $\frac{2}{3} \overline{X}_1 + \frac{1}{3} \overline{X}_2$, es $\frac{1}{15}$. Justifica este resultado.
Si la ponderación es inversamente proporcional a sus tamaños de muestra y se afirma que la varianza muestral de tal estimación ponderada, $\frac{1}{\overline{X}_1} + \frac{2}{\overline{X}_2}$, es $\frac{1}{10}$. Justifica este resultado.

Para estimar la media de la población:
1. Un hombre pondera los promedios de las muestras en proporción a sus tamaños de muestra y afirma que la varianza muestral de tal estimación ponderada, $\frac{2}{3} \overline{X}_1 + \frac{1}{3} \overline{X}_2$, es $\frac{1}{15}$. Justifica este resultado.
2. Un segundo hombre simplemente promedia los promedios muestrales y utiliza $\frac{1}{2} (\overline{X}_1 + \overline{X}_2)$. Muestra que la varianza muestral de tal estimación es $\frac{3}{40}$.
3. Muestra que ambos métodos son imparciales (tienen una media igual a la verdadera media $\mu$).
4. Explica (a) desde el punto de vista de una muestra de tamaño 15.
Dada una población de 500 que está compuesta por dos subpoblaciones o estratos. El estrato 1 tiene 400 miembros y el estrato 2 tiene 100 miembros. Se toma una muestra aleatoria de tamaño 20 de cada estrato. El promedio de la muestra del estrato 1 es 4.0 y la desviación estándar de esta muestra es 1.0. El promedio de la muestra del estrato 2 es 8.0 y la desviación estándar de esta muestra es 2.0.
1. Estima la media total de la población.
2. Estima la desviación estándar de la estimación de la media total.
¿Cuál de las siguientes afirmaciones es verdadera? En el muestreo, a medida que el tamaño de la muestra aumenta, la desviación estándar de la distribución teórica de los promedios muestrales (a) disminuye en valor, acercándose a 0; (b) aumenta en valor, creciendo sin límite; (c) no aumenta ni disminuye necesariamente, pero se aproxima al valor de la verdadera desviación estándar (universal).
Se lanza una moneda justa $n$ veces. Cada vez que sale cara, se suma $a$ a la puntuación, cada vez que sale cruz se resta $b$ de la puntuación. Determina la media y la varianza de la distribución de la puntuación después de $n$ lanzamientos.
Supón que los pesos al nacer de los niños se distribuyen normalmente con una media de 7 libras y una desviación estándar de $\frac{1}{2}$ libra. Supón que ambos sexos tienen igual probabilidad y que el peso al nacer es independiente del sexo.
1. ¿Cuál es la probabilidad de que la cuarta observación en una familia de cuatro sea un varón?
2. ¿Cuál es la probabilidad de que todas las observaciones sean varones?

¿Cuál es la probabilidad de que los cuatro niños, cualquiera que sea su sexo, tengan un peso al nacer promedio superior a 7.5 libras?
1. ¿Cuál es la probabilidad de que los niños sean todos varones y tengan un peso al nacer promedio superior a 7.5 libras?
2. ¿Estás utilizando una suposición no declarada? Si es así, ¿cuál?
En un experimento de habilidades motoras, 100 sujetos realizan una tarea en 25 grupos seleccionados al azar de 4, pero cada sujeto tiene un cubículo separado, de modo que no influye en los otros miembros del grupo. A partir de la distribución de frecuencia de las puntuaciones de estos 100 sujetos, el experimentador encuentra que la media es de 30 puntos y la desviación estándar de 10 puntos. Luego, el experimentador obtiene para cada uno de los 25 grupos la suma de las puntuaciones de los 4 sujetos. Quiere saber:
1. el valor de la media de las 25 sumas,
2. el valor de la desviación estándar de las 25 sumas.
Dile la respuesta a (a) exactamente. Usando los datos dados y tu conocimiento de la teoría en este capítulo, haz una buena estimación del resultado para (b).

Al escuchar el resultado de la desviación estándar de las sumas para los grupos, el experimentador se sorprende. Él dice: "La ley de los promedios debería haber hecho que la desviación estándar para los grupos fuera menor, no mayor, que la desviación estándar de las puntuaciones individuales". Comenta concisamente sobre su error de comprensión.

Valores de \(X\):	-4, -1, 2, 3
Valores de \(Y\):	-3, -1, 2, 3
Valores de \(Z\):	-2, -1, 0, 3