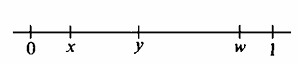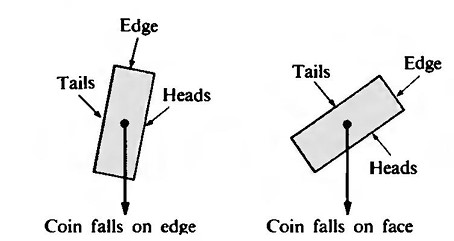
Problema 38 del libro de Mosteller

La Moneda Gruesa

¿Qué grosor debe tener una moneda para tener una probabilidad de 1/3 de caer de canto?

Al escuchar esta pregunta por primera vez, el gran matemático fallecido John von Neumann, fue lo suficientemente cruel como para resolverla, incluyendo una respuesta con tres decimales en su cabeza en 20 segundos en presencia de algunos desafortunados que habían trabajado mucho más tiempo.

Este problema no tiene una respuesta definitiva sin algunas condiciones simplificadoras. La elasticidad de la moneda, la intensidad con la que se lanza y las propiedades de la superficie sobre la que aterriza combinan para hacer que la pregunta en la vida real sea una cuestión empírica.

En lugar de lanzar puntos sobre un intervalo unitario, dejemos caer cuatro puntos sobre una circunferencia de unidad; en lugar de tres puntos, dejemos caer cuatro y llamemos al cuarto uno z.

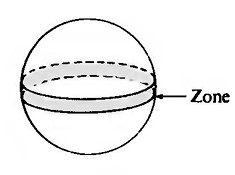
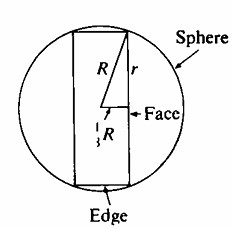
Un teorema clave en la geometría sólida simplifica este problema. Cuando los planos paralelos cortan una esfera, la banda de forma de naranja formada entre ellos se llama zona. El área de la superficie de una zona es proporcional a la distancia entre los planos, y así nuestra moneda debería ser ¹/₃ tan gruesa como la esfera. ¿Cómo debería compararse el grosor con el diámetro de la moneda?

Sea R el radio de la esfera y r el de la moneda.

El teorema de Pitágoras da

\( R^2 = r^2 + \frac{1}{9} R^2 \)

o

\( R^2 = \frac{9}{8} r^2 \)

por lo tanto

\( R = r \sqrt{\frac{9}{8}} \)

\( r = R \sqrt{\frac{8}{9}} \)

por lo tanto

\( r = R \frac{\sqrt{8}}{3} \)

y

r ≈ 0.354 R.

Y así la moneda debería tener aproximadamente el 35% del grosor del diámetro de la moneda.

Digresión: Una Nota sobre el Principio de Simetría cuando se Dejan Caer Puntos en una Línea

Supongamos que varios puntos se dejan caer al azar en el intervalo unitario de 0 a 1. Por ejemplo, supongamos w, x, y son estos puntos como se muestra en la figura. Estos tres puntos dividen el intervalo en cuatro segmentos con longitudes x, y − x, w − y, y 1 − w. Cuando tres puntos se dejan caer repetidamente, cada gota produce cuatro segmentos, y cada segmento (el más a la izquierda, el segundo, el tercero y el más a la derecha) tiene una distribución entre estas gotas. Es fácil encontrar la distribución acumulativa de la longitud del punto más a la izquierda. Considere algún número t. ¿Cuál es la probabilidad de que los tres puntos caigan a la derecha de t? Dado que los tres puntos se dejan caer de forma independiente y cada uno tiene una probabilidad de 1 − t de caer a la derecha de t, la respuesta es (1 − t)³. Por lo tanto,

P(el punto más a la izquierda está a la derecha de t) = (1 − t)³.

Ejemplo. ¿Cuál es la posición mediana del punto más a la izquierda? La mediana es la posición que se excede la mitad del tiempo. Queremos (1 − t)³ = ¹/₂. El valor apropiado de t es dado por

1 − t = \(\sqrt[3]{\frac{1}{2}}\),

y así t ≈ 0.206.

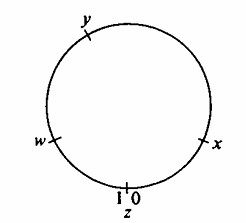
Si bien el cálculo de la distribución de la longitud del segmento más a la izquierda es fácil, y podrías obtener el más a la derecha por simetría, podrías quedarte perplejo al encontrar la distribución para el segundo o tercer segmento. Puede que ya hayas adivinado que son iguales a los del segmento más a la izquierda, pero la mayoría de las personas no lo hacen. El propósito de las siguientes observaciones es hacer que esa proposición sea razonable.

En lugar de dejar caer puntos en un intervalo unitario, dejémoslos caer sobre un círculo de circunferencia unidad; en lugar de tres puntos, dejemos caer cuatro y llamemos al cuarto uno z.

Así, los puntos x, y, w se dejan caer al azar en un intervalo unitario como antes, pero no tiene una escala sobre él. Dejamos caer el cuarto punto z, también al azar. Los cuatro puntos han sido tratados por igual, y los cuatro segmentos del círculo, aquí (zx), (xy), (yw), y (wz), surgen de un proceso equitativo para todos los segmentos. Imagina dejar caer cuatro puntos muchas veces y cada vez obtener la distancia desde z al primer punto en sentido contrario a las agujas del reloj, desde allí al siguiente, y así sucesivamente. Entonces generaríamos cuatro distribuciones de longitudes de segmentos, y estas distribuciones serían iguales a través de muchos grupos de 4 puntos.

Ahora para cada caída, corta el círculo en z, y enderézalo en un intervalo unitario etiquetando los extremos 0 y 1 como se implica en la figura. La caída de cuatro puntos en un círculo usando z como un corte es equivalente a la caída de tres puntos en el intervalo unitario.

Aunque aún puedas tener dudas persistentes, no daremos una prueba formal, pero sí enunciaremos el principio.

Principio de Simetría: Cuando n puntos se dejan caer al azar en un intervalo, las longitudes de las n + 1 líneas de segmentos tienen distribuciones idénticas.