Figuras a partir de Figuras
Haciendo Aritmética y Álgebra con Geometría
Los patrones proporcionan demostraciones claras
Podemos aprender mucho de aritmética simplemente escribiendo los números en filas de 1, 2, 3, ..., como se muestra en la Figura 2.1. La columna de la izquierda en cada sección es la lista de múltiplos de la cantidad de entradas en cada fila.
Cuando escribimos solo dos números en cada fila, la columna izquierda contiene los números pares (Figura 2.2) y la columna derecha contiene los números impares (Figura 2.3).

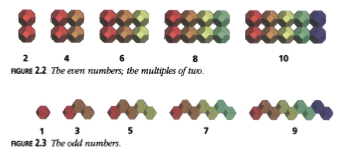
Figura 2.3: Los números impares.
Las columnas de números en la Figura 2.1 son las clases residuales, o conjuntos de números que dejan el mismo residuo (o resto) cuando se dividen por el número de entradas en una fila. En nuestras figuras, las clases residuales están diferenciadas por colores. Por ejemplo, la columna central (naranja) en la tercera sección de la Figura 2.1 contiene números que son uno más que un múltiplo de 3, es decir, números que son congruentes a 1 módulo 3. Una de las contribuciones más importantes de Carl Friedrich Gauss (1777–1855) a la teoría de números fue la aritmética de las clases residuales. Decimos que dos números son congruentes módulo \(n\) cuando la diferencia entre ellos es divisible por \(n\).
Por ejemplo, en 1938, el 3 de mayo, el 10 de mayo, el 17 de mayo, el 24 de mayo y el 31 de mayo fueron martes; los números 3, 10, 17, 24 y 31 son todos congruentes módulo 7.
La regla del 9
Una línea triple de igual \( \equiv \) se usa para denotar congruencia. Por ejemplo, módulo \(9\),
\( 1 \equiv 10 \equiv 100 \equiv 1000 \equiv \ldots \)
y esta es la base del preuve par neuf, o "la regla del 9", una herramienta útil de aritmética. Para usar la regla del 9 en un número, simplemente suma sus dígitos, restando \(9\) cuando sea necesario. Para verificar tus sumas, restas y multiplicaciones, repite este proceso para cada uno de los números involucrados y también para el resultado. Por ejemplo, obtenemos cinco al dividir \(469\) entre \(9\), lo que nos muestra que deberíamos obtener el mismo resultado si aplicamos este método.
Los colores revelan patrones
Cuando coloreamos una sección de la Figura 2.1 con los colores de otra, las clases residuales forman patrones regulares. Si la longitud de la fila es impar, entonces los números impares (naranja) y pares (rojo) forman un patrón de tablero de ajedrez (Figura 2.4).
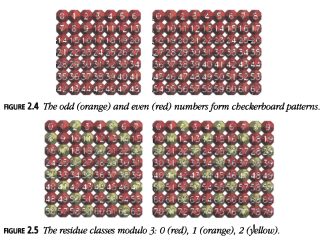
Figura 2.5: Las clases residuales módulo 3: 0 (rojo), 1 (naranja), 2 (amarillo).
Si el módulo, es decir, el número de columnas, no es un múltiplo de 3, las clases residuales módulo 3 (rojo, naranja, amarillo) aparecen como franjas diagonales (Figura 2.5).
Módulo 4, las clases residuales (rojo, naranja, amarillo, verde) forman columnas o diagonales (izquierda y derecha de la Figura 2.6), o cuando la longitud de la fila es un número par sencillo, \(4n + 2\), como 6 o 10 (es decir, divisible por 2, pero no por 4) crean un diseño similar a los movimientos de los caballos en ajedrez (centro de la Figura 2.6).
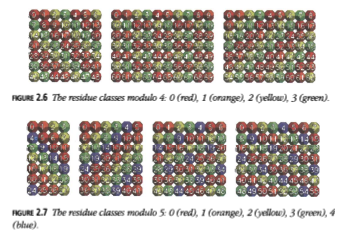
Figura 2.7: Las clases residuales módulo 5: 0 (rojo), 1 (naranja), 2 (amarillo), 3 (verde), 4 (azul).
Los movimientos del caballo son especialmente notables para las clases residuales módulo 5, siempre que la longitud de la fila sea congruente a \(\pm2\) módulo 5 (dos secciones a la derecha de la Figura 2.7).
Números cuadrados
Si recogemos los múltiplos de 1, 2, 3, ..., de modo que las primeras columnas de cada sección de la Figura 2.1 se unan en una sola tabla, obtenemos la tabla de multiplicar (Figura 2.8), cuya diagonal principal nos da los números cuadrados (Figura 2.9).
La tabla de multiplicar y los números cuadrados
La tabla de multiplicar tiene los números cuadrados como su diagonal principal (Figura 2.8).
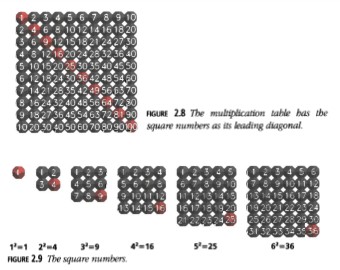
Figura 2.9: Los números cuadrados.
¿En qué clases residuales se encuentran los números cuadrados? La Figura 2.10 nos muestra las respuestas para módulo 5, 7 y 8. La Figura 2.10(a) es la misma que la Figura 2.1(c), solo que los números cuadrados están coloreados en rojo.

Propiedades de los números cuadrados
A partir de la Figura 2.10(c), vemos que:
Veremos otra prueba interesante de esto después de conocer los números triangulares (Figura 2.23).
La Figura 2.11 muestra que los cuadrados son siempre congruentes a 0, 1 o 4 módulo 5 (cuenta los puntos rojos).

Tal vez hayas notado en la Figura 2.10 que los cuadrados se encuentran sobre parábolas, que son las curvas que obtienes al dibujar gráficos de expresiones cuadráticas o polinomios de grado dos, como las expresiones algebraicas para los cuadrados, números triangulares y otros números figurados "bidimensionales" que pronto veremos. Pero antes de dejar los cuadrados, observa la Figura 2.12.

Números Triangulares
Ahora escribimos los números en filas de longitud creciente (Figura 2.13), de modo que los gnomones sean simplemente las filas (Figura 2.14). Esto nos da los números triangulares.
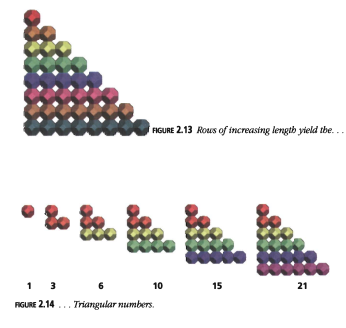
Figura 2.14: ... los números triangulares.
Los antiguos griegos llamaban gnomón (conocedor del tiempo) a la pieza que puedes agregar a una figura para producir una figura más grande de la misma forma. Los gnomones de la Figura 2.12 se combinan para mostrar que la suma de los primeros \(n\) números impares es el \(n\)-ésimo cuadrado, \(n^2\). La adición de un gnomón más ilustraría la identidad:
\( n^2 + (2n + 1) = (n + 1)^2 \)
Llamaremos al \(n\)-ésimo número triangular \(\Delta_n\). ¿Qué tan grande es? Si colocamos dos números triangulares con lado \(n\) juntos, forman un rectángulo, de \(n + 1\) por \(n\), por lo que la respuesta es \(\frac{1}{2}n(n + 1)\). La Figura 2.15 muestra el caso para \(n = 6\).
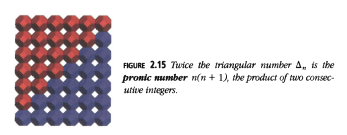
Algunos lectores preferirán las pruebas algebraicas de este hecho, por inducción. Para probar que:
\( 1 + 2 + \ldots + n = \frac{1}{2}n(n + 1) \)
comprobamos el caso inicial y luego suponemos el resultado para el número anterior, es decir:
\( 1 + 2 + \ldots + (n - 1) = \frac{1}{2}(n - 1)n = \frac{1}{2}n^2 - \frac{1}{2}n \).
Al sumar \(n\) a ambos lados, de hecho obtenemos:
\( \left( \frac{1}{2}n^2 - \frac{1}{2}n \right) + n = \frac{1}{2}n^2 + \frac{1}{2}n = \frac{1}{2}n(n + 1) \).
Dado que dos números consecutivos, uno es impar y el otro es par, no es sorprendente que su producto sea siempre divisible por 2.
De manera similar, podemos demostrar que la suma de los primeros \(n\) números impares es \(n^2\), deduciendo:
\( 1 + 3 + 5 + \ldots + (2n - 1) + (2n + 1) = n^2 + 2n + 1 \)
\( = (n + 1)^2 \)
a partir de:
\( 1 + 3 + 5 + \ldots + (2n - 1) = n^2 \).
Alternativamente, podríamos haber usado el mismo dispositivo que en la Figura 2.15 para mostrar esto (Figura 2.16). De hecho, este método "tubo-organizado" será útil en muchos otros contextos.
La suma de números impares
La suma de los primeros \(n\) números impares es el cuadrado de \(n^2\), como se muestra en la Figura 2.16.
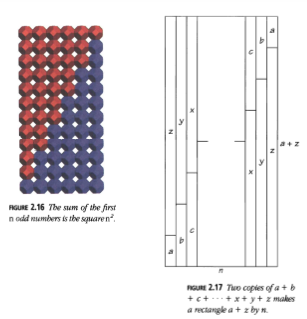
Figura 2.17: Dos copias de \(a + b + c + \ldots + x + y + z\) forman un rectángulo de \(z + z\) por \(n\).
La Figura 2.17 muestra cómo encontrar la suma de cualquier progresión aritmética, o secuencia de números espaciados de manera uniforme:
Por ejemplo, la suma de los primeros 10 términos:
\( 5 + 8 + 11 + \ldots + 32 = 10 \times \frac{5 + 32}{2} = 185. \)
Esto funciona porque \(a + z = b + y = c + x = \ldots\).
Sumando números impares
Podemos comprobar nuevamente que la suma de los números impares consecutivos, comenzando desde 1, da los cuadrados (Figura 2.18a). Si, en lugar de comenzar desde 1 cada vez, continuamos donde nos quedamos antes (Figura 2.18b), entonces obtenemos lo siguiente:

Si sumamos todos los números impares en las primeras \(n\) filas de la Figura 2.18(b), vemos que la suma de los primeros \(n\) cubos es igual a la suma de los primeros \(n\) números impares, lo cual sabemos que es \(\Delta_n^2\):
\( 1^3 + 2^3 + 3^3 + \ldots + n^3 = \left( \frac{1}{2}n(n + 1) \right)^2 \).
Si hubiéramos adivinado este resultado, podríamos haberlo deducido por inducción del caso anterior sumando \(n^2\) a ambos lados:
\( 1^3 + 2^3 + \ldots + (n - 1)^3 = \frac{1}{4}n^4 - \frac{1}{2}n^3 + \frac{1}{4}n^2 \).
Triángulos consecutivos
La Figura 2.19 muestra que la suma de dos números triangulares consecutivos forma un cuadrado.

Más patrones con números triangulares
La Figura 2.20 muestra cómo dos números triangulares consecutivos forman un cuadrado. En símbolos, esto puede escribirse como:
\(\Delta_n + \Delta_{n-1} = 1 + 2 + 3 + \ldots + n \)
\( = 1 + 3 + 5 + \ldots + (2n - 1)\).
Usaremos este patrón más adelante (en la Figura 2.38) para sumar los primeros \(n\) cuadrados y nuevamente (en la Figura 2.49) para sumar los primeros \(n\) cubos.
Las Figuras 2.21, 2.22 y 2.23 muestran algunas relaciones adicionales entre los números triangulares.
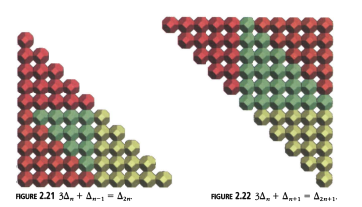
Figura 2.22: \(3\Delta_n + \Delta_{n+1} = \Delta_{2n+1}\).
Relaciones entre números triangulares
La Figura 2.23 muestra que:
\( (2n + 1)^2 = 8\Delta_n + 1 = \Delta_{n-1} + 6\Delta_n + \Delta_{n+1} \).
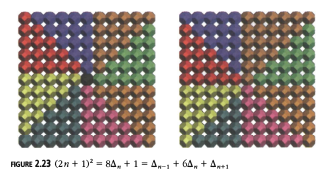
Esta figura también muestra una vez más que un cuadrado impar es congruente a 1 módulo 8.
¿Qué números triangulares son también cuadrados? Por ejemplo:
0, 1, 36, 1225, ... ?
Tendremos que esperar hasta estudiar la ecuación de Pell en el Capítulo 7 antes de poder responder esa pregunta.
Números Poligonales
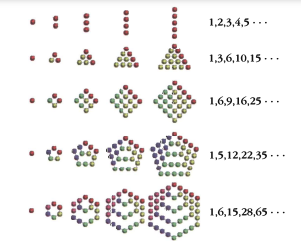
Obtenemos diferentes tipos de números poligonales sumando los primeros \(n\) términos de progresiones aritméticas apropiadas que comienzan con 1, así:
\( 1 + 1 + 1 + 1 +\ldots \text{da: } 1, 2, 3, 4,\ldots \)
\( 1 + 2 + 3 + 4 +\ldots \text{da triangulares: } 1, 3, 6, 10,\ldots \)
\( 1 + 3 + 5 + 7 +\ldots \text{da cuadrados: } 1, 4, 9, 16,\ldots \)
\( 1 + 4 + 7 + 10 +\ldots \text{da pentagonales: } 1, 5, 12, 22,\ldots \)
\( 1 + 5 + 9 + 13 +\ldots \text{da hexagonales: } 1, 6, 15, 28,\ldots \)
\( 1 + 6 + 11 + 16 +\ldots \text{da heptagonales: } 1, 7, 18, 34,\ldots \)
\( 1 + 7 + 13 + 19 +\ldots \text{da octogonales: } 1, 8, 21, 40,\ldots \)
Ya hemos conocido los primeros tres tipos.
Números Poligonales
Observa que el número de lados en el polígono es dos más que la diferencia común. Pronto veremos, como en la Figura 2.24 y también en el Capítulo 4 sobre números de Catalán, que es dos más que el número de triángulos que componen el polígono. El tercer número de cada secuencia siempre es divisible por 3, y el quinto número por 5: ¿el séptimo siempre será divisible por 7?
Estos números poligonales obtienen sus nombres de arreglos de puntos (Figura 2.24), que han sido estudiados desde al menos la época de Pitágoras (ca. 540 a.C.).
Cada secuencia en la Figura 2.24 puede formarse a partir de la fila anterior añadiendo un triángulo de \(\Delta_{n-1}\) puntos de un color nuevo a la izquierda de cada polígono. Ya sabemos que:
\(n + \Delta_{n-1} = \Delta_n \), el número triangular, y que
\(\Delta_n + \Delta_{n-1} = n + 2\Delta_{n-1} = n^2\), el cuadrado, y esto continúa:
\(n^2 + \Delta_{n-1} = n + 3\Delta_{n-1} = \frac{1}{2}n(3n-1)\), el número pentagonal,
\(n + 4\Delta_{n-1} = n(2n - 1)\), el número hexagonal,
y así sucesivamente.
Más sobre números hexagonales
El número \(p\)-lateral con \(n\) puntos en cada lado es:
\(n + (p - 2)\Delta_{n-1} = \frac{1}{2}pn(n - 1) - n(n - 2).\)
Por ejemplo, el \(n\)-ésimo número hexagonal es:
\(n + 4\Delta_{n-1} = \Delta_n + 3\Delta_{n-1}.\)
Como puedes ver en la Figura 2.25, que también muestra (compara con la Figura 2.22) que:
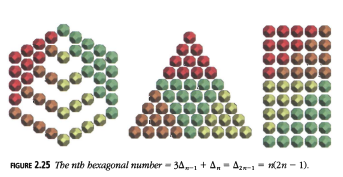
De hecho, solo los números triangulares impares generan números hexagonales.
Números Pentagonales y Hexagonales
Es fácil probar algebraicamente que:
\( 3 \times \frac{1}{2} n(3n - 1) = \frac{1}{2}(3n - 1)(3n). \)
Geométricamente, aplana la "parte superior" de cada número pentagonal en la cuarta fila de la Figura 2.24 para crear un trapecio equilátero (forma de cubeta); verás que puedes formar rompecabezas triangulares con tres copias de cada uno.
Algunas personas han usado el nombre "números hexagonales" para los representados en la Figura 2.26, pero usaremos el nombre de Martin Gardner, números hex, para distinguirlos.
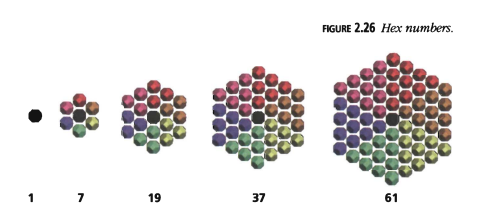
De la Figura 2.23 podemos ver que el \(n\)-ésimo número hexagonal es:
\(\text{hex}_n = 1 - 3n + 3n^2.\)
Observa que:
\(\text{hex}_{n+1} = 1 + 6\Delta_n = 1 + 3n + 3n^2,\)
y que los números hexagonales son congruentes a 1 módulo 6.
Números Cuadrados Centrados
Los números cuadrados centrados (Figura 2.27) forman un patrón similar, mostrando que son congruentes a 1 módulo 4, lo cual también se deduce del hecho de que son la suma de dos cuadrados consecutivos (Figura 2.28), uno de los cuales es par y el otro impar.
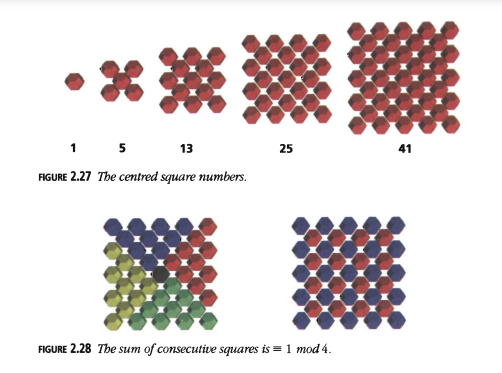
Figura 2.28: La suma de cuadrados consecutivos es \(\equiv 1 \mod 4\).
La Tercera Dimensión
Supongamos que apilamos los números hex como pirámides hexagonales (Figura 2.29). ¡Sorpresa! Obtenemos los cubos, \(n^3\) (Figura 2.30), quizás los números figurados tridimensionales más simples, que normalmente construiríamos apilando cuadrados \(n \times n\).
¿Por qué las pirámides hexagonales son iguales a los cubos? Podemos ver esto en la Figura 2.31, donde \(n = 4\). Los hexágonos que usamos para crear los números hexagonales son proyecciones, o sombras, de cubos. Obtenemos el cubo de tamaño \(n + 1\) comenzando con una fila roja de \(n\) puntos (Figura 2.31(a)) y construyendo hacia afuera 3 varillas amarillas de \(n\) puntos cada una (Figura 2.31(b)). Luego, los 3 espacios entre las varillas acomodan una pared verde de \(n \times n = n^2\) puntos (Figura 2.31(c)), y tenemos un patrón perfectamente ajustado.
Pirámides Hexagonales y Cubos
Podemos apilar los números hexagonales como pirámides hexagonales (Figura 2.29). ¡Sorpresa! Obtenemos los cubos, \(n^3\) (Figura 2.30), quizás los números figurados tridimensionales más simples, que normalmente construiríamos apilando cuadrados \(n \times n\).
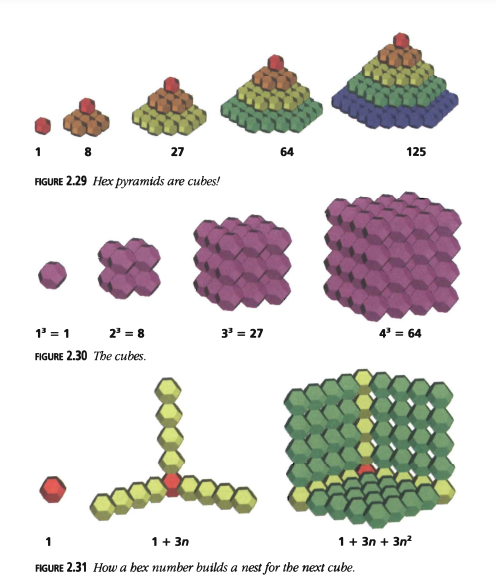
Figura 2.30: Los cubos.
Figura 2.31: Cómo un número hexagonal construye un nido para el siguiente cubo.
¿Por qué las pirámides hexagonales son iguales a los cubos? Podemos verlo en la Figura 2.31, donde \(n = 4\). Los hexágonos que usamos para crear los números hexagonales son proyecciones, o sombras, de cubos. Obtenemos el cubo de tamaño \(n + 1\) comenzando con una fila roja de \(n\) puntos (Figura 2.31(a)) y construyendo hacia afuera 3 varillas amarillas de \(n\) puntos cada una (Figura 2.31(b)). Luego, los 3 espacios entre las varillas acomodan una pared verde de \(n \times n = n^2\) puntos (Figura 2.31(c)), creando un patrón perfectamente ajustado.
Este patrón encierra cuidadosamente (3 caras adyacentes) un cubo de \(n \times n \times n\), completándolo a \((n + 1)^3\). Este es un caso muy especial:
\(1 + 3n + 3n^2 + n^3 = (1 + n)^3\),
del teorema binomial, que veremos en el Capítulo 3.
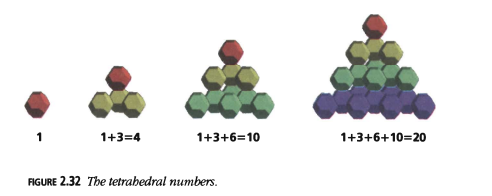
Números Tetraédricos
Podemos apilar otros números figurados bidimensionales para hacer números tridimensionales. Por ejemplo, los números triangulares pueden apilarse para formar pirámides triangulares, o números tetraédricos.
La Figura 2.32 muestra los primeros cuatro números tetraédricos. ¿Cuál es el \(n\)-ésimo número tetraédrico? Si eres bueno en rompecabezas tridimensionales, entonces hay algunas maneras ingeniosas de empaquetar 6 copias del \(n\)-ésimo número tetraédrico en una caja de \(n \times (n + 1) \times (n + 2)\), mostrando que la respuesta es:
\(T_{et_n} = \frac{1}{6}n(n + 1)(n + 2)\).
Pero aquí hay una forma de verlo sin aventurarse en tres dimensiones. Suma todos los números en las tres copias del patrón triangular en la Figura 2.33. Obtenemos un patrón triangular de quince 7 (nota que 7 es 2 más que 5) y de manera similar, tres veces el \(n\)-ésimo número tetraédrico es el \(n\)-ésimo número triangular de \((n + 2)\)s, de modo que:
box\(T_{et_n} = \frac{1}{6}n(n + 1)(n + 2)\).
Suma de Números Triangulares
La Figura 2.33 muestra cómo sumar números triangulares de forma sencilla. Observamos que sumar tres copias de los números triangulares crea un patrón fácil de calcular.
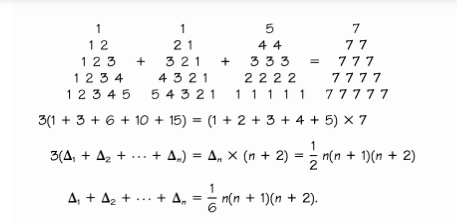
Los números tetraédricos son enteros, por lo tanto:
El tercer triángulo de números en la Figura 2.33 puede verse como el quinto número tetraédrico colocado sobre uno de sus bordes. Podemos sumar los números leyendo las capas:
\((1 \times 5) + (2 \times 4) + (3 \times 3) + (4 \times 2) + (5 \times 1) = 35,\)
y de manera general:
\((1 \times n) + (2 \times (n - 1)) + (3 \times (n - 2)) + \ldots + ((n - 1) \times 2) + (n \times 1) = T_{et_n}\).
Tabla de Multiplicación y Números Tetraédricos
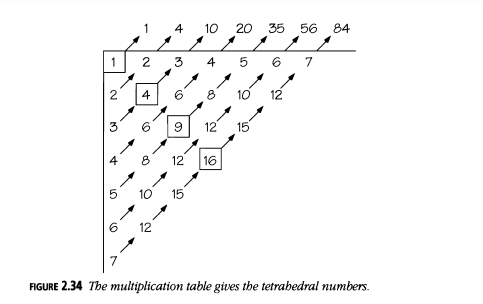
Otra forma de ver esto es sumar las diagonales de la tabla de multiplicación (Figura 2.34; compárese con la Figura 2.8). Dado que la tabla de multiplicación es simétrica, los números tetraédricos son pares, excepto que los cuadrados a lo largo de la diagonal principal son alternadamente impares y pares, haciendo que cada cuarto número tetraédrico sea impar, comenzando desde el primero:
\(1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, \ldots\).
Números Tetraédricos Truncados
Si tomamos el número tetraédrico \((3n - 2)\) y eliminamos el número tetraédrico \((n - 1)\) de cada esquina, nos queda el \(n\)-ésimo número tetraédrico truncado (Figura 2.35):
\(T_{tet_n} = T_{et_{3n-3}} - 4T_{et_{n-1}} = \frac{1}{6}n(23n^2 - 27n + 10).\)
Números Piramidales Cuadrados
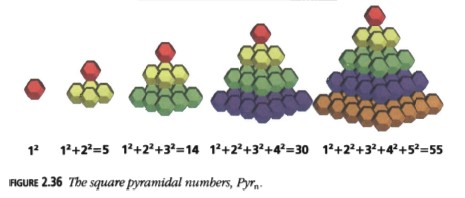
Ahora hagamos algunas pirámides cuadradas. Los antiguos monumentos de guerra a veces tienen una pila de bolas de cañón organizadas como una pirámide cuadrada: \(1 + 4 + 9 + \ldots + n^2\). Este es el \(n\)-ésimo número piramidal, \(Pyr_n\).
También puedes crear una forma diferente de "pirámide cuadrada" usando bloques de construcción para niños (apilándolos con las esquinas de los cuadrados uno sobre otro; ver Figura 2.36). Ahora intenta empaquetar seis de estas pirámides en una caja rectangular de dimensiones \(n \times n + 1 \times 2n + 1\). Si tienes éxito, habrás demostrado que:
\(1^2 + 2^2 + 3^2 + \ldots + n^2\),
es igual a: \[ \frac{1}{6}n(n + 1)(2n + 1). \]

Formas Alternativas para Verlo
Aquí hay tres maneras más fáciles de ver esto:
- Vimos en la Figura 2.19 que la suma de dos números triangulares consecutivos es un cuadrado: \[ \Delta_{n-1} + \Delta_n = n^2, \] así que la suma de dos números tetraédricos consecutivos es un número piramidal cuadrado: \[ Tet_{n-1} + Tet_n = Pyr_n, \] \[ \frac{1}{6}(n - 1)n(n + 1) + \frac{1}{6}n(n + 1)(n + 2) = \frac{1}{6}n(n + 1)(2n + 1). \]
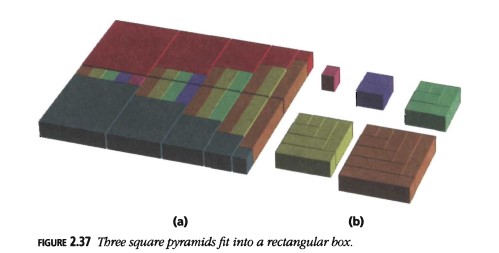
- Empaca las capas de dos (rojo y azul claro) pirámides cuadradas en una caja rectangular poco profunda, con ancho \(2n + 1\) y largo \(\Delta_n\), el \(n\)-ésimo número triangular, como en la Figura 2.37(a). Divide el espacio restante en tiras, que encajan como en la Figura 2.12 para formar las capas cuadradas de una tercera pirámide cuadrada (Figura 2.37(b)). Por lo tanto, un número piramidal cuadrado, \(Pyr_n\), es: \[ \frac{1}{3}\Delta_n \times (2n + 1) = \frac{1}{6}n(n + 1)(2n + 1), \] como antes.
Suma de Números Triangulares para Crear Cuadrados
Finalmente, en la Figura 2.38 hay \( (2 \times 5) + 1 = 11 \) columnas, cada una conteniendo el número triangular:
\(1 + 2 + 3 + 4 + 5 = \frac{1}{2} \times 5 \times (5 + 1).\)
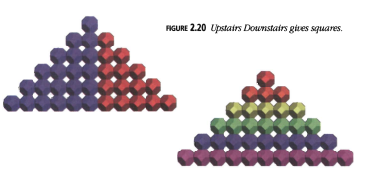
Las cinco filas sobre la línea suman \(1^2, 2^2, 3^2, 4^2, 5^2\) siguiendo la regla de Subir-Bajar (Figura 2.20). Cada uno de los dos triángulos debajo de la línea, cuando se suman diagonalmente, también contiene los primeros cinco cuadrados:
\(3 \times (1^2 + 2^2 + 3^2 + 4^2 + 5^2) = (1 + 2 + 3 + 4 + 5) \times 11,\)
\(3 Pyr_n = \Delta_n \times (2n + 1).\)
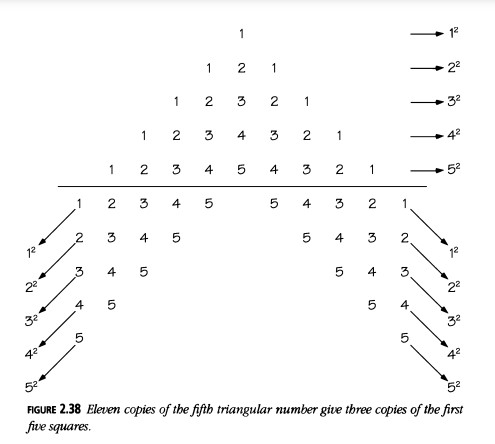
Números Octaédricos
La manera más fácil de ver los números octaédricos (Figura 2.39) es como pirámides cuadradas dobles, la suma de dos pirámides cuadradas consecutivas:
\(Oct_n = Pyr_{n-1} + Pyr_n = \frac{1}{3}n(2n^2 + 1).\)
Son la suma de los números en las siguientes matrices, donde los "1s" son los "polos" del octaedro:
Las diferencias entre los números octaédricos consecutivos son los números cuadrados centrados que vimos en la Figura 2.27:

1, 6, 19, 44, 85, 146, ...
Diferencias: 1, 5, 13, 25, 41, 61, ...
Números Stella Octangula
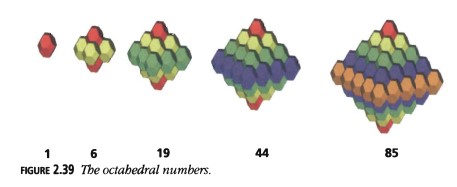
Si tomamos un número octaédrico con arista \(n\) y añadimos un número tetraédrico de arista \(n - 1\) en cuatro caras alternas, obtenemos un número tetraédrico de arista \( (n - 1) + 1 + (n - 1) = 2n - 1\), como se muestra en la Figura 2.40.
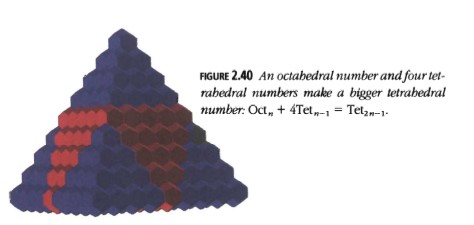
Si añadimos otros cuatro tetraedros en las otras cuatro caras, obtenemos un número stella octangula (Figura 2.41) nombrado en honor a la stella octangula de Kepler:
\(Stel_n = Oct_n + 8Tet_{n-1} = n(2n^2 - 1).\)
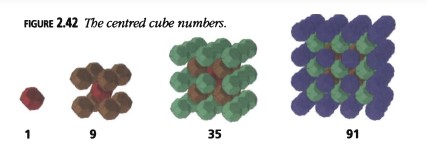
Números de Cubos Centrados
Los análogos tridimensionales de los números cuadrados centrados son los números de cubos centrados (Figura 2.42):
\(Ccub_n = n^3 + (n - 1)^3 = (2n - 1)(n^2 - n + 1).\)
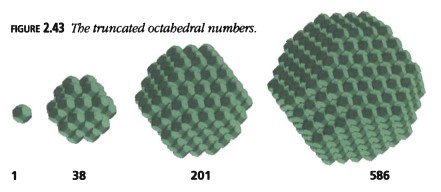
Números Octaédricos Truncados
Comenzamos con el número octaédrico \((3n - 2)\), \(Oct_{3n-2}\), y eliminamos la pirámide cuadrada \((n - 1)\), \(Pyr_{n-1}\), de cada uno de sus seis vértices. Nos quedan los números octaédricos truncados (Figura 2.43):
\(Toct_n = Oct_{3n-2} - 6Pyr_{n-1} = \frac{1}{3}(3n - 2)(2(3n - 2)^2 + 1) - \frac{6}{6}(n - 1)n(2n - 1).\)
\(= 16n^3 - 33n^2 + 24n - 6.\)
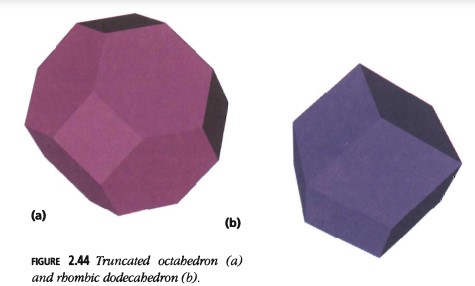
Números Dodecaédricos Rómbicos
¿Cuáles son los análogos tridimensionales de los números hexagonales? El \(n\)-ésimo número hexagonal, \(hex_n\), cuenta el número de celdas en un empaque de panal que están a menos de \(n\) pasos de distancia desde una celda central (el punto negro en la Figura 2.26).
Entre los sólidos Platónicos (regulares) y Arquimedianos (semi-regulares), los únicos que llenan exactamente el espacio tridimensional son el cubo (obviamente) y el octaedro truncado, Figura 2.44(a). En este empaquetamiento mediante octaedros truncados, el nexo de todas las celdas que están a menos de \(n\) pasos forma la figura de un dodecaedro rómbico, Figura 2.44(b).
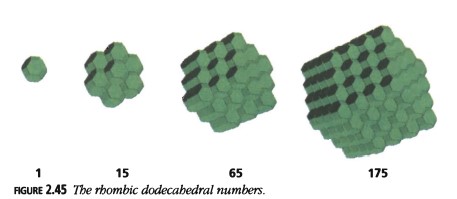
Definición de los Números Dodecaédricos Rómbicos
Los números tridimensionales correspondientes son los números dodecaédricos rómbicos (Figura 2.45). Una forma de visualizar un número dodecaédrico rómbico es agregar una pirámide cuadrada a cada una de las seis caras de un cubo centrado:
\(Rho_n = Ccub_n + 6Pyr_{n-1} = (2n - 1)(2n^2 - 2n + 1).\)
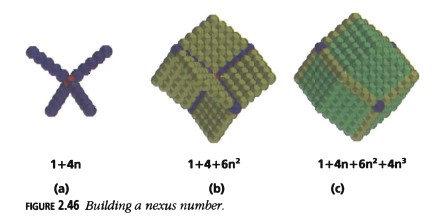
Números Nexus
La Figura 2.46 muestra cómo construir los números nexus. Comenzamos con una celda roja central y agregamos cuatro varillas de longitud \(n\) en caras alternas (Figura 2.46(a)). Luego añadimos 6 paredes amarillas, cada una con \(n^2\) celdas, entre pares de varillas (Figura 2.46(b)). Finalmente, insertamos 4 bloques verdes de \(n^3\) celdas en las esquinas formadas por tres paredes (Figura 2.46(c)).
Números nexus similares están definidos en todas las dimensiones:

Dimensión | Número Nexus \(n+1\)
0 | 1 — La unidad
1 | \(1 + 2n\) — Números impares
2 | \(1 + 3n + 3n^2\) — Números hexagonales
3 | \(1 + 4n + 6n^2 + 4n^3\) — Números dodecaédricos rómbicos
4 | \(1 + 5n + 10n^2 + 10n^3 + 5n^4\) — Siguientes números nexus
Deformando el Siguiente Número Nexus
En la Figura 2.12 doblamos cada número nexus unidimensional (números impares) en un gnomon y apilamos estos gnomons para formar cuadrados. En la Figura 2.31 doblamos los números hexagonales en "nidos" y luego los apilamos para formar cubos. De manera similar, en cuatro dimensiones podemos doblar los números dodecaédricos rómbicos en nidos que se apilan para formar cubos tetradimensionales, o tesseractos. Para la mayoría de nosotros, esto es un poco difícil de visualizar, pero:
\( odd_1 + odd_2 + \ldots + odd_n = n^2, \)
\( hex_1 + hex_2 + \ldots + hex_n = n^3, \)
\( Rho_1 + Rho_2 + \ldots + Rho_n = n^4, \)
y:
\( Rho_{n+1} = 1 + 4n + 6n^2 + 4n^3, \)
es justamente lo necesario para aumentar \(n^4\) a \((n + 1)^4\). Si has adelantado temas, habrás notado la conexión con el teorema binomial en el próximo capítulo.
La Cuarta Dimensión
Existen otros números figurados en dimensiones superiores. Aunque es difícil visualizar rompecabezas en cuatro dimensiones, ¡se puede hacer! Supongamos que quieres apilar los primeros cinco números tetraédricos para formar los números pentatópicos (Figura 2.47). El pentatopo es la figura regular más simple en cuatro dimensiones.

1 = \(Ptop_1\)
1 + 4 = 5 = \(Ptop_2\)
1 + 4 + 10 = 15 = \(Ptop_3\)
1 + 4 + 10 + 20 = 35 = \(Ptop_4\)
1 + 4 + 10 + 20 + 35 = 70 = \(Ptop_5\)
1 + 4 + 10 + 20 + 35 + 56 = 126 = \(Ptop_6\)
Visualizando los Números Pentatópicos
La Figura 2.48 muestra cómo apilar cuatro copias de los primeros cinco números tetraédricos para formar números pentatópicos. Estos números suman \((5 + 3)\) veces la suma de los primeros cinco números triangulares.

Números Pentatópicos
Cuatro copias de los primeros cinco números tetraédricos suman el quinto número tetraédrico, \(Tet_5\).
En general, cuatro copias de los primeros \(n\) números tetraédricos suman \(n + 3\) veces el \(n\)-ésimo número tetraédrico:
\( \frac{1}{6} n(n+1)(n+2) \).
\( Ptop_n = \frac{1}{4} Tet_n \times (n+3) = \frac{1}{24} n(n+1)(n+2)(n+3). \)
Suma de Cubos
También podríamos usar un rompecabezas tetradimensional para apilar cubos y formar una pirámide cúbica, pero la tabla de multiplicación de la Figura 2.8 nos salva de esto. La Figura 2.49 es la tabla de multiplicación, equipada con gnomons como en la Figura 2.12.
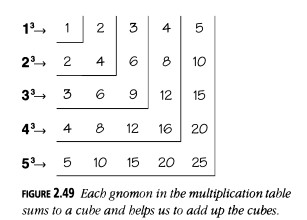
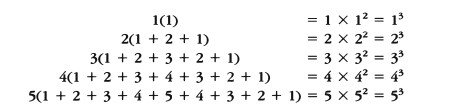
Los gnomons contienen:
\( 1(1) = 1 \times 1^2 = 1^3 \)
\( 2(1 + 2 + 1) = 2 \times 2^2 = 2^3 \)
\( 3(1 + 2 + 3 + 2 + 1) = 3 \times 3^2 = 3^3 \)
\( 4(1 + 2 + 3 + 4 + 3 + 2 + 1) = 4 \times 4^2 = 4^3 \)
\( 5(1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1) = 5 \times 5^2 = 5^3 \)
Usando la regla de Subir-Bajar (Figura 2.20), el total de números en la tabla de multiplicación es exactamente el producto:
\((1 + 2 + 3 + 4 + 5)(1 + 2 + 3 + 4 + 5) = \Delta_n^2 \)
Entonces, como vimos en la Figura 2.18(b):
\( 1^3 + 2^3 + 3^3 + \cdots + n^3 \)
es igual al cuadrado del \(n\)-ésimo número triangular:
Conclusión
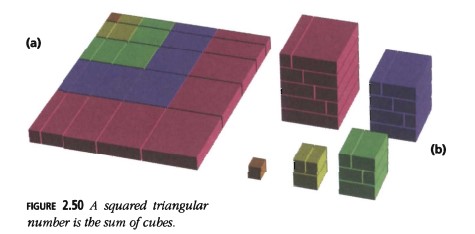
La Figura 2.50 muestra esto como un rompecabezas tridimensional fácil. El cuadrado de lado \(1 + 2 + 3 + 4 + 5 = 15\) de la parte (a) se divide en rectángulos que se reensamblan para formar cinco cubos (b).
Más y Más Dimensiones
Podemos seguir apilando pirámides triangulares en más y más dimensiones. El método que usamos en las Figuras 2.29 y 2.45 se extiende para mostrar que:
\( 1 + 1 + 1 + \cdots + 1 = n \)
\( 1 + 2 + 3 + \cdots + n = \frac{1}{2} n (n + 1) \)
\( 1 + 3 + 6 + \cdots + \frac{1}{2} n (n + 1) = \frac{1}{6} n (n + 1) (n + 2) \)
\( 1 + 4 + 10 + \cdots + \frac{1}{6} n (n + 1) (n + 2) = \frac{1}{24} n (n + 1) (n + 2) (n + 3) \)
Dándonos los números contables, triangulares, tetraédricos y pentatópicos; y aunque nos hayamos quedado sin nombres, nunca nos quedaremos sin dimensiones: los primeros números sin nombre
\( \frac{1}{120} n (n + 1) (n + 2) (n + 3) (n + 4) \)
demuestran que:
Algunos Números Muy Grandes
Los cuadrados se hacen grandes rápidamente; los cubos y las potencias superiores se expanden aún más rápido; y \(n^n\) crece más rápidamente que todos los números figurados. Sin embargo, los matemáticos a veces necesitan incluso números más grandes y desean alguna forma de escribirlos.
Las computadoras usan \(m \uparrow n\) para imprimir \(m^n\) y así evitar superíndices (aunque hoy solo parece permanecer la notación con flechas). Esto sugiere la siguiente notación práctica:
\(m \uparrow n\) o \(mn\) significa \(m^n\), y
\(m \uparrow \uparrow n\) significa \(m^{m^{\cdots^m}} \), con \(n\) copias de \(m\) evaluadas desde la derecha.

Aunque la notación \(m \uparrow \uparrow \cdots \uparrow n\) solo fue introducida en 1976 por Donald Knuth, una función esencialmente similar fue definida por W. Ackermann en 1928, y así llamaremos:
\(1 \uparrow 1, 2 \uparrow \uparrow 2, 3 \uparrow \uparrow \uparrow 3, 4 \uparrow \uparrow \uparrow \uparrow 4, \ldots\)
Los números de Ackermann. El primer número de Ackermann es 1, el segundo es \(2 \uparrow \uparrow 2 = 2^2 = 4\), y el tercero es:
\(3^{3^3} = 7625597484987\),
donde el número de treses es \(3^3\).
\(4^{4^{4^{4}}}\),
Donde el número de cuatros es \(4^{4^{4}}\), y este equivale a \(4^{256}\) (un número de 155 dígitos).
Graham's Number
número de Graham wikipediaNuestra propia notación de "números encadenados" nombra números aún más grandes. En esta, \(a \uparrow \uparrow \ldots \uparrow \uparrow b\) (con \(c\) flechas) se llama \(a \to b \to c\).
\(a \to b \to c = a \to b \to \cdots \to b \to y - 1\),
definido como:
- \(a \cdot \cdot \cdot x = x\) si \(y = 1\),
- \(a \cdot \cdot \cdot x \to (a \cdot \cdot \cdot) x = y = 2\).
Graham's Number se encuentra en algún lugar entre \(3 \to 3 \to 64 - 2\) y \(3 \to 64 \to 3 - 2\).
El Número de Skewes
Este número es mucho más pequeño que \(4^{4^{4}}\), el cual es menos que \(5^{55}\) o \(5 \uparrow 3\).
Números Muy Grandes
El número \(10^{10^{34}}\) fue conocido como el número de Skewes. Sin embargo, se ha demostrado que este número ya no es candidato para teoremas especiales como el de Graham.
Referencias
- W. Ackermann, "Zum Hilbertschen Aufbau der reellen Zahlen", Math. Annalen, 99 (1928): 118–133.
- Martin Gardner, Second Book of Mathematical Puzzles and Diversions, W. H. Freeman, New York, 1961; Chapter 4, "Digital Roots".
- Martin Gardner, Time Travel and Other Mathematical Bewilderments, W. H. Freeman, New York, 1988; Chapter 2, "Hexes and Stars".
- Martin Gardner, Penrose Tiles to Trapdoor Ciphers, W. H. Freeman, New York, 1989; Chapter 17, "Ramsey Theory".
- P. Goodwin, "A Polyhedral Series or Two", Math. Gaz., 69 (1985): 191–197.
- Harvey Hindin, "Stars, Hexes, Triangular Numbers and Pythagorean Triples", J. Recreational Math., 16 (1983–84): 191–193.
- Edward Kasner and James Newman, Mathematics and the Imagination, G. Bell & Sons, London, 1949, p. 23.
- Donald E. Knuth, "Mathematics and Computer Science: Coping with Finite Numbers", Science, (1976): 12–17.
¿Qué sigue?
Esperamos que te gusten los problemas en los que alguien te da una intrigante secuencia de números y te pregunta qué sigue. En este capítulo, te daremos varias maneras de descubrirlo. La mayoría de estas maneras implican construir algún tipo de patrón a partir de tus números. El triángulo de Pascal es un patrón muy conocido.
Si eres como nosotros, también disfrutarás jugar con secuencias de números por el puro gusto de hacerlo, así que también te mostraremos algunos juegos numéricos que a menudo usan patrones para transformar mágicamente una secuencia en otra. Uno de los más interesantes se describe a continuación.
La magia de Moessner
Alfred Moessner descubrió que algunas de nuestras secuencias favoritas pueden encontrarse de una forma sorprendente. Comienza con los números consecutivos y rodea cada segundo número; luego forma la suma acumulativa de los números no rodeados y verás los cuadrados:

Si en lugar de rodear cada segundo número, rodeas cada tercer número, totaliza lo que queda (rodeando el último número de cada bloque) y suma los números no rodeados (hexagonales), verás los cubos:

Rodeando cada cuarto número:
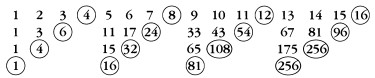
Conduce de manera similar a las cuartas potencias, y así sucesivamente. Entonces, rodeando los números:
\(n + n + n + n + n + n + n + \ldots\)
ha llevado a los números:
\(n \times n \times n \times n \times n \times n \ldots\)
Si rodeamos cada número triangular, \(1 + 2 + 3 + \ldots + n\):
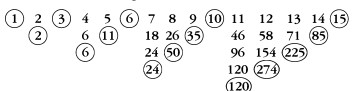
Obtenemos los números factoriales, \(1 \times 2 \times 3 \times \ldots \times n\), de los que hablaremos pronto.
¿Y si rodeamos los cuadrados?
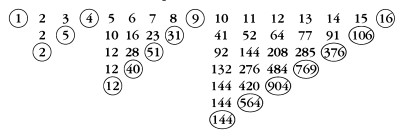
Números Factoriales
Si estos números te desconciertan, observa que los cuadrados son:
\[ 1 \\ 1 + 2 + 1 \\ 1 + 2 + 3 + 2 + 1 \\ 1 + 2 + 3 + 4 + 3 + 2 + 1 \ldots \]
Y que los números finales rodeados son:
\[ 1 \times 2 \times 1 \\ 1 \times 2 \times 3 \times 2 \times 1 \\ 1 \times 2 \times 3 \times 4 \times 3 \times 2 \times 1 \]
La regla general es que si comienzas rodeando:
\[ 1a, \; 2a + 1b, \; 3a + 2b + 1c, \; 4a + 3b + 2c + 1d, \ldots \]
Entonces los números finales rodeados son:
\[ 1^a, \; 2^a \times 1^b, \; 3^a \times 2^b \times 1^c, \; 4^a \times 3^b \times 2^c \times 1^d \ldots \]

Acabamos de ver cómo podemos obtener los números factoriales con la magia de Moessner y, de hecho, ya los encontramos en el Capítulo 2 cuando apilamos pirámides triangulares en más dimensiones.
Números de Arreglos
El factorial \(n\) es el número de arreglos, o órdenes, o permutaciones de \(n\) cosas en fila. ¿Cuántos arreglos hay de \(r\) objetos, elegidos de \(n\) cosas diferentes? El primero puede ser cualquiera de los \(n\), el segundo puede ser cualquiera de los restantes \(n - 1\), el tercero cualquiera de los restantes \(n - 2\), y así sucesivamente, hasta que el \(r\)-ésimo sea cualquiera de los \(n - r + 1\). El número total de arreglos diferentes es:
\[ n \times (n - 1) \times (n - 2) \times \ldots \times (n - r + 1), \]
El producto de todos los números desde \(1\) hasta \(n\), excepto para aquellos de \(1\) a \(n - r\), así que podemos expresar esto concisamente usando números factoriales:
\[ \frac{n!}{(n - r)!} \]
El número de arreglos de \(r\) cosas tomadas de \(n\) es:
\[ \frac{n!}{(n - r)!} \]
Números de Elección
Si solo nos interesa el número de elecciones, o combinaciones, de \(r\) cosas elegidas entre \(n\), entonces no distinguimos entre las maneras factoriales \(r!\) en que podríamos haberlas ordenado en fila. Así que, para obtener los números de elección:
\[ \binom{n}{r}, \]
dividimos los números de arreglos entre \(r!\):
El número de elecciones de \(r\) cosas entre \(n\) es:
\[ \binom{n}{r} = \frac{n!}{r!(n - r)!} \]
En esta fórmula, puedes intercambiar \(r\) por \(n - r\) sin alterar el valor. El número de maneras de elegir 5 cosas de entre 8 es el mismo que el número de maneras de elegir las 3 que quieres dejar fuera:
\[ \binom{8}{5} = \binom{8}{3} \]
Y en general:
\[ \binom{n}{r} = \binom{n}{n - r}. \]
Ahora supón que estás en la clase y quieres saber si estás en el equipo. ¿De cuántas maneras puedes ser incluido? Si estás en el equipo, los otros 10 deben ser elegidos de los otros 27:
\[ \binom{27}{10} = 8436285 \text{ maneras}. \]
¿Y de cuántas maneras no estás incluido? Todos los 11 deben ser elegidos de los otros 27:
\[ \binom{27}{11} = 13037895 \text{ maneras}. \]
Por lo tanto:
\[ \binom{28}{11} = \binom{n - 1}{r} + \binom{n - 1}{r - 1}. \]
El Triángulo de Pascal
Esta es una manera muy simple de generar los números de elección. Comienza desde:
\[ \binom{0}{0} = 1 \text{ en la fila 0, y } \binom{1}{0} = 1 \text{ y } \binom{1}{1} = 1 \text{ en la fila 1}, \]
y calcula filas sucesivas poniendo:
\[ \binom{n}{0} = 1 \text{ y } \binom{n}{n} = 1 \text{ en cada extremo,} \]
y formando cada otro número como la suma de los dos en la fila inmediatamente anterior (Figura 3.2).
Las primeras filas de números de elección se muestran en la Figura 3.2. La matriz en la Figura 3.3 se conoce generalmente como el Triángulo de Pascal, porque fue estudiado intensamente por Blaise Pascal (1623-1662), el famoso filósofo y matemático francés. Ya había sido descrito mucho antes por matemáticos chinos y por Omar Khayyam, quien murió en 1123.
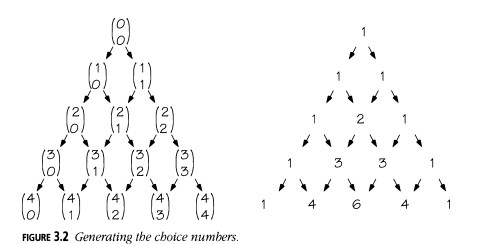
Por supuesto, hemos visto algunos de estos números antes, en el Capítulo 2, cuando apilamos pirámides triangulares en más y más dimensiones. Los números al comienzo de cada fila son solo unos:
\(1, 1, 1, 1, 1, 1, 1, 1, 1, \ldots\).
Los segundos números en cada fila son los números contables:
\(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, \ldots\).

Los terceros números son los números triangulares:
\(1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, \ldots\).
Los cuartos números son los números tetraédricos:
\(1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, \ldots\).
Los quintos son los números pentatópicos:
\(1, 5, 15, 35, 70, 126, 210, 330, 495, 715, 1001, \ldots\).
Y así sucesivamente. Los números en cada diagonal son las sumas acumulativas de los de la diagonal anterior.
Números de Elección con Repeticiones
¿De cuántas maneras puedes elegir cinco elementos de \(n\), si se permiten repeticiones? En otras palabras, ¿cuántos tipos esencialmente diferentes de "manos de póker" hay, si ignoramos colores y escaleras y estamos jugando con un mazo doble, de modo que puedas tener un repóker?
| Mano de póker | 13 en un palo | \(n\) cartas en un mazo |
|---|---|---|
| Todos diferentes | \(\binom{13}{5} = 1287\) | \(\binom{n}{5}\) |
| Un par | \(13 \times \binom{12}{3} = 2860\) | \(n \times \binom{n - 1}{3}\) |
| Dos pares | \(\binom{13}{2} \times 11 = 858\) | \(\binom{n}{2} \times (n - 2)\) |
| Tres iguales | \(13 \times \binom{12}{2} = 858\) | \(n \times \binom{n - 1}{2}\) |
| Full house (3 & 2) | \(13 \times 12 = 156\) | \(n \times (n - 1)\) |
| Cuatro iguales | \(13 \times 12 = 156\) | \(n \times (n - 1)\) |
| Repóker | 13 = 13 | \(n\) |
| Total | \(\binom{17}{5} = 6188\) | \(\binom{n + 4}{5}\) |
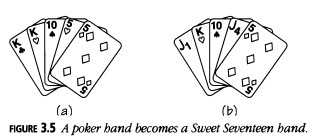
Seguramente una respuesta tan simple puede encontrarse más fácilmente. De hecho, las manos corresponden al número de manos de 5 cartas elegidas de un mazo de Sweet Seventeen de 17 cartas distinguibles: A, K, Q, J, 10, 9, 8, 7, 6, 5, 4, 3, 2 y cuatro comodines indistinguibles: J1, J2, J3 y J4.
Si te reparten una mano de Sweet Seventeen (Figura 3.4(a)), ordénala de la manera habitual, de menor a mayor, pero con cualquier comodín en las posiciones que corresponden a sus etiquetas (Figura 3.4(b)). Luego, conviértela en una mano de póker reemplazando cualquier comodín por copias de la primera carta genuina que los siga: la Figura 3.4(c) muestra el full house resultante, nueves sobre doses.

Para ver cómo la correspondencia es exacta, convierte tus manos de póker clasificadas (Figura 3.5(a)) en una mano de Sweet Seventeen reemplazando todos los duplicados de cartas más adelante por comodines, etiquetados por su posición contando desde la izquierda (Figura 3.5(b)).
En general, para encontrar el número de elecciones de \( r \) cosas de \( n \) diferentes, pero con repeticiones permitidas, imagina que estás jugando Sweet Seventeen, pero en lugar de un mazo de 13 + 4 comodines, tienes un mazo de \( n + (r - 1) \) comodines, y la respuesta es:
Números de elección son coeficientes binomiales
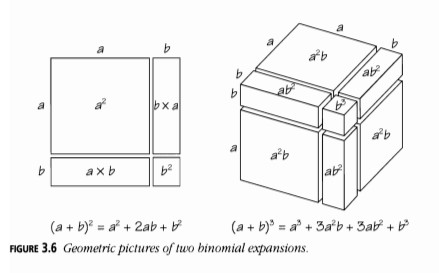
La Figura 3.6 te ayudará a realizar dos de las manipulaciones algebraicas en la Figura 3.7, donde los números, o coeficientes, que aparecen son exactamente los del triángulo de Pascal.
Puedes ver por qué esto es así si etiquetas los \( b \) de esta manera:
Expansiones Binomiales
Cada término en la derecha proviene de elegir ya sea a o b de cada uno de los binomios \((a + b)\) en la izquierda. El número de términos con r bs y \(n - r\) as es el número de formas de elegir r bs entre el total de n bs, es decir: \[ \binom{n}{r}. \] Así hemos probado el Teorema Binomial:
Debido a que hay dos opciones de cada uno de los n factores binomiales, el número total de productos es \(2^n\). Verificamos esto sumando las filas del triángulo de Pascal:
- 1 = \(2^0\)
- 1 + 1 = \(2^1\)
- 1 + 2 + 1 = \(2^2\)
- 1 + 3 + 3 + 1 = \(2^3\)
- 1 + 4 + 6 + 4 + 1 = \(2^4\)
- 1 + 5 + 10 + 10 + 5 + 1 = \(2^5\)
- 1 + 6 + 15 + 20 + 15 + 6 + 1 = \(2^6\)
Este es el resultado de establecer \(a = b = 1\) en el teorema binomial. Si dejas \(a = 1\) y \(b = -1\), obtendrás lo siguiente:
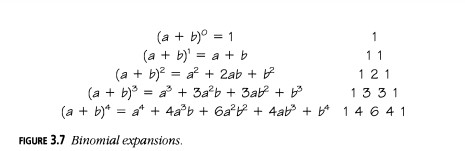
Patrones de Frisos
En la Figura 3.8(a), hemos dibujado un patrón delimitado por un zigzag de ceros en los bordes izquierdo y derecho, y líneas horizontales de ceros arriba y abajo. En la Figura 3.8(b), hemos usado unos en lugar de ceros. Ahora llena los signos de interrogación siguiendo la regla de que los números a y d en cada pequeño diamante:
b
a d
c
Para la suma (Figura 3.8(a)):
\(a + d = b + c + 1\)
Para la multiplicación (Figura 3.8(b)):
\(a \cdot d = b \cdot c + 1\)
Algunas cosas sorprendentes ocurren, como se muestra en la Figura 3.9(a) y (b). Para el patrón aditivo, parte (a), los siguientes ceros en cada línea forman una copia del zigzag inicial, por lo que el patrón se repite cada siete filas.
Para el patrón multiplicativo, parte (b), los ceros forman un patrón diferente, reflejando el hecho de que las reglas de multiplicación y suma producen resultados distintos.

El patrón multiplicativo, parte (b), es aún más sorprendente: todas las divisiones son exactas, lo que permite que las entradas sean números enteros. Esta vez, los unos en cada fila forman una copia invertida del zigzag inicial. Hay que recorrer un total de nueve posiciones en cada fila antes de obtener una repetición exacta.
Lo mismo ocurre con anchuras y formas arbitrarias del zigzag inicial, como puedes verificar por experimento. ¿Puedes descubrir por qué ocurre esto?
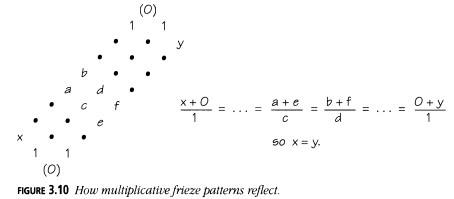
Para los patrones de frisos multiplicativos, la observación esencial es que para cualquier conjunto de seis entradas como:
b
a d
c f
e
tenemos que \((a + e)/c = (b + f)/d\). La Figura 3.10 muestra cómo esto implica que un número \(x\) justo por encima de la fila superior de unos reaparecerá algún tiempo después, justo debajo de dicha fila.

¿Cuántas regiones?
De vez en cuando, alguien propone una secuencia de trucos donde la regla general no es lo que parece a simple vista.
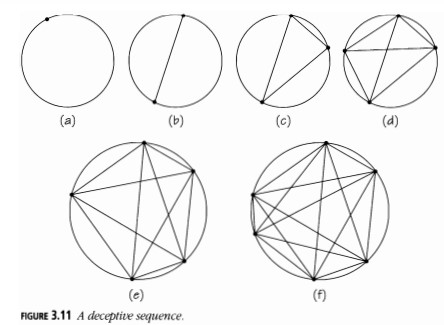
¿Cuántas regiones hay dentro de los seis círculos en la Figura 3.11? El \(n\)-ésimo círculo tiene \(n\) puntos en el perímetro, unidos de todas las maneras posibles, asegurándose de que no más de dos líneas pasen por un punto interior.
Vemos que las respuestas son \(1, 2, 4, 8, 16\) para los primeros cinco círculos. Son obviamente potencias de dos. Si ejerces un poco más de cuidado en el último caso, puedes hacer que llegue a \(32\). Y podrías querer verificar que con \(10\) puntos la respuesta llega a \(256\).
Tratemos de probar que la respuesta para \(n\) puntos es \(2^{n-1}\). Dado que \(2^{n-1}\) es el número de subconjuntos de los números \(1, 2, \dots, n - 1\), podemos hacer esto dando una regla que asigne dicho subconjunto a cada región.
Etiquetamos los puntos \(0, 1, 2, \dots, n - 1\) en sentido antihorario alrededor del círculo (Figura 3.12). Porque queremos terminar con un subconjunto de \(\{1, 2, \dots, n - 1\}\), el dígito \(0\) tiene solo un estado temporal: siempre lo omitimos al final.
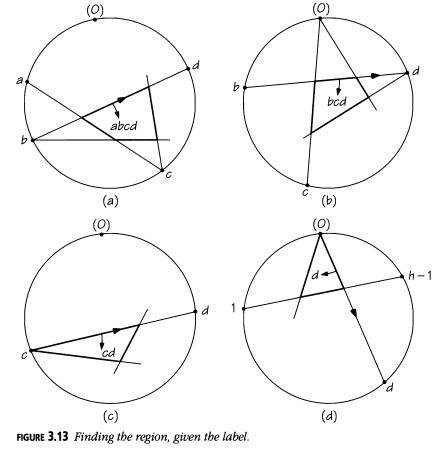
Aquí está cómo encontrar la región correspondiente a un conjunto de números. El punto de encuentro para un conjunto de números \(a, b, c, d\) (\(a < b < c < d\)) es donde las cuerdas \(ac\) y \(bd\) se intersectan. El punto de encuentro de un conjunto de dos números, \(c < d\), es el más pequeño de los dos.
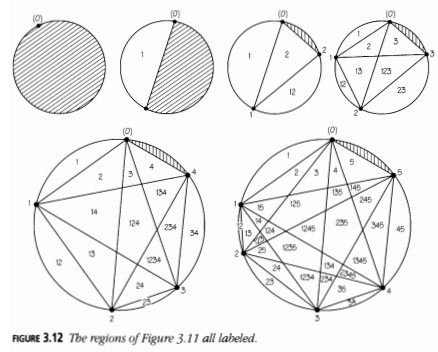
Para encontrar una región dada su etiqueta, mira a lo largo del rayo hacia \(d\), el número más grande del conjunto. Entonces, la región está a tu derecha. Por ejemplo, si \(0 < a < b < c < d\), entonces la etiqueta \(abcd\) se asigna a la región que se muestra en la Figura 3.13(a); pero si \(a = 0\), como en la Figura 3.13(b), la región se etiqueta como \(bcd\), eliminando el \(0\). Si \(0 < c < d\), damos la etiqueta \(cd\) a la región que se muestra en la Figura 3.13(c); y si \(c = 0\), como en la Figura 3.13(d), simplemente etiquetamos la región como \(d\). Esto deja sin etiquetar la región a tu izquierda cuando estás en \(0\) y miras a lo largo del rayo hacia \(n - 1\). Esto corresponde al conjunto vacío y se muestra sombreado en las Figuras 3.13(d) y 3.13(e).
¿Qué tan cuidadoso eras?
Te dijimos que obtendrías la respuesta 32 para el círculo de 6 puntos si usabas un poco más de cuidado. Sin embargo, usando solo un poco más de cuidado, encontrarás la respuesta 31. Lo que no encontrarás es una región etiquetada 12345. Las etiquetas contienen solo \(0, 1, 2, 3, 4\) números, por lo que el número de regiones no es \(2^{n-1}\), sino más bien la suma de los primeros cinco términos:
\[ \binom{n-1}{0} + \binom{n-1}{1} + \binom{n-1}{2} + \binom{n-1}{3} + \binom{n-1}{4} \]
en la expansión binomial de \((1 + 1)^{n-1}\). Estos son todos los términos para \(n\) hasta \(5\). Cuando \(n = 6\), el último término
\[ \binom{6-1}{5} = 1, \]
falta, y para valores mayores de \(n\), la respuesta se queda cada vez más corta. Las respuestas correctas son, para
\(n = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14\) regiones \(= 1, 2, 4, 8, 16, 31, 57, 99, 163, 256, 386, 562, 794, 1093\).
Adivinando el siguiente término de una secuencia
Como acabamos de ver, en algunos problemas es fácil adivinar la respuesta incorrecta. Pero si siempre adivinas mal, fallarás esa prueba vital de inteligencia. Aquí hay algunas técnicas que pueden guiarte hacia la respuesta correcta.
Diferenciando
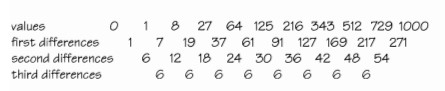
Tomemos la secuencia que acabamos de encontrar e intentemos calcular el siguiente término, suponiendo que no sabíamos cómo encontrar la fórmula general anteriormente.
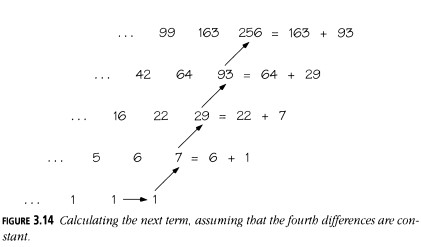
Preparamos una tabla de diferencias en la cual cada entrada es la diferencia entre las dos entradas justo encima de ella (en el sentido de "derecha menos izquierda"). Verás que en nuestro caso:
Valores: \(1, 2, 4, 8, 16, 31, 57, 99, 163\)
Primeras diferencias: \(1, 2, 4, 8, 15, 26, 42, 64\)
Segundas diferencias: \(1, 2, 4, 7, 11, 16, 22\)
Terceras diferencias: \(1, 2, 3, 4, 5, 6\)
Cuartas diferencias: \(1, 1, 1, 1, 1, 1\)
Las cuartas diferencias son todas iguales. Podemos adivinar que este patrón continúa para siempre y usar esta conjetura para calcular el próximo término trabajando hacia arriba (Figura 3.14).
Esto sugiere correctamente que para un círculo con 10 puntos, el número de regiones debe ser 256. Verificamos esto observando que exactamente la mitad de los \(2^9\) subconjuntos de \(\{1, 2, \ldots, 9\}\) tienen como máximo cuatro miembros.
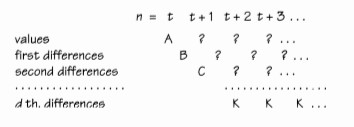
Algo de álgebra muestra que si comenzamos con la secuencia de valores de un polinomio de grado \(d\), entonces su primera secuencia de diferencias serán los valores de un polinomio de grado \(d-1\), su segunda secuencia de diferencias serán los valores de un polinomio de grado \(d-2\), y su \(d\)-ésima secuencia de diferencias serán los valores de algún...
Diferencias y Potencias
Por ejemplo, hagamos diferencias en la secuencia de cubos:
La Útil Pequeña Fórmula de Newton
Cuando encuentras diferencias constantes, ¿cómo calculas el polinomio? Puedes encontrar la respuesta formando las diferencias para los coeficientes binomiales, \( \binom{n}{0}, \binom{n}{1}, \binom{n}{2}, \dots \).

Si observas los números destacados, verás que la secuencia con la tabla de diferencias de forma:

Es:
\[ A \binom{n}{0} + B \binom{n}{1} + C \binom{n}{2} + D \binom{n}{3}, \]es decir,
\[ A + Bn + \frac{1}{2} Cn(n-1) + \frac{1}{6} Dn(n-1)(n-2). \]Por ejemplo, cuando hicimos diferencias de los cubos, encontramos que:
- \( A = 0 \),
- \( B = 1 \),
- \( C = 6 \),
- \( D = 6 \).
Y:
\[ 0 \binom{n}{0} + 1 \binom{n}{1} + 6 \binom{n}{2} + 6 \binom{n}{3} = 0 + n + 3n(n-1) + n(n-1)(n-2) = n^3. \]Un patrón similar funciona para polinomios de grado superior. Si, comenzando desde el término d-ésimo, obtienes una tabla en la que las diferencias de grado d son todas \( K \):
¿Cuántos triángulos?
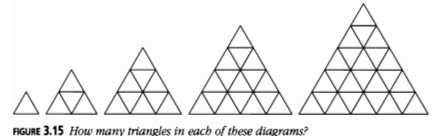
Una buena manera de encontrar el n–ésimo término es contar los primeros pocos con mucho cuidado y luego hacer una tabla de diferencias. Si dibujas más figuras como las que hemos hecho en la Figura 3.15, y cuentas todos los triángulos (incluyendo los triángulos invertidos) encontrarás los números y sus diferencias son:

Las terceras diferencias alternan entre 2 y 1, por lo que la respuesta se da alternativamente por dos expresiones:
\[ \frac{n(n + 2)(2n + 1)}{8} \quad \text{para } n \text{ par, y} \quad \frac{n(n + 2)(2n + 1) - 1}{8} \quad \text{para } n \text{ impar}. \]Diferenciación
Incluso cuando tu secuencia no proviene de un polinomio, la diferenciación a menudo es informativa. Las Figuras 3.16 y 3.17 muestran cómo las potencias de 2, y los números de Fibonacci (de los que aprenderemos más en el próximo capítulo), se repiten a sí mismos cuando se diferencian.


Entonces, si como en la Figura 3.18, alguna fila de otra tabla de diferencias se convierte en potencias de 2, la secuencia original difiere de las potencias de 2 solo por los valores de un polinomio. Esto es similar para otras secuencias de potencias y para los números de Fibonacci también.

Ventiladores de diferencias de Jackson
Robert Jackson sugiere que si has completado una tabla de diferencias y aún no entiendes la secuencia, deberías girar el papel en un ángulo de 60°, por ejemplo, y empezar de nuevo, y tal vez repetir esto varias veces para hacer un ventilador de tablas de diferencias.
Jackson descubrió que este proceso de abanico convierte potencias de 4 en potencias de 3, luego en potencias de 2, potencias de 1 y finalmente potencias de 0 (Figura 3.19). En general, la secuencia \(k^n\), multiplicada por cualquier polinomio en \(n\), se reduce a ceros mediante un ventilador de diferencias \(k\)-doble.
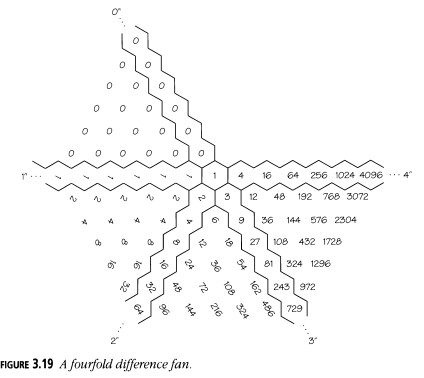
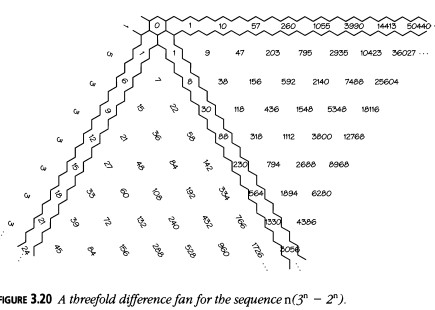
Es una buena idea probar un ventilador de diferencias en cualquier secuencia que sospeches que se da mediante una fórmula simple que implique potencias de los primeros números. La Figura 3.20 muestra lo que sucede con una de esas secuencias.
Muros numéricos
Si sospechas que tu secuencia no es un polinomio, pero se calcula mediante un tipo de regla de "autoarranque" que define los números de Fibonacci (donde cada término es la suma de los dos términos anteriores), puedes detectar esto mediante un muro numérico (o "tabla de cocientes-diferencias") en lugar de una tabla de diferencias ordinaria.
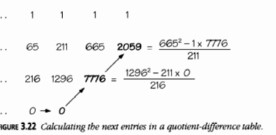
La fila superior de un muro numérico (por ejemplo, Figura 3.21) es una cadena de unos, y debajo de estos colocamos los términos de tu secuencia sospechosa. Las entradas adicionales se calculan mediante la regla de que para cada cruce de cinco números adyacentes,
\[ X^2 = NS + EW. \]Entonces, si alguna fila consta completamente de ceros, tu secuencia sospechosa es efectivamente una secuencia de autoarranque, en la que cada término puede calcularse como la suma de múltiplos fijos de los \(k\) términos anteriores, donde:

Muros con Ventanas
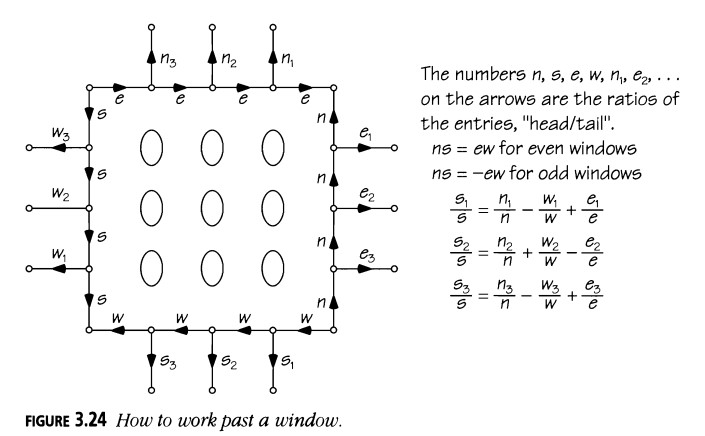
Nuestra regla para los muros numéricos no está completa, porque a veces tendrás que dividir entre cero. Fred Lunnon nos habló por primera vez de la notable verdad de que los ceros en un muro numérico forman "ventanas" cuadradas bordeadas por progresiones geométricas. La Figura 3.23 muestra un ejemplo. Para obtener los números justo debajo de una ventana, debes usar otra regla, explicada en la Figura 3.24.
Es más fácil trabajar alrededor de un cero aislado:
Usando el hecho de que:
\[ S' / N' + N / S^2 = E' / W' + W / E^2. \]
Como puedes ver en la Figura 3.23, el muro numérico para los números de Fibonacci menos uno tiene algunas ventanas, por lo que se necesita una regla más complicada para calcular las entradas marcadas con estrellas. Todas las entradas en el muro numérico de una secuencia de números serán números enteros. Así como en los patrones de friso, esto proporciona una verificación útil para tu aritmética.
¿Qué haces si encuentras una secuencia de números y...

... deseas verificar si siguen una regla geométrica? Consulta la Figura 3.24.
Si no sabes qué son, puedes buscar en la maravillosa obra de Sloane & Plouffe Encyclopedia of Integer Sequences, o enviar un correo a sequences@research.att.com con una línea que diga, por ejemplo:
lookup 1 1 2 3 5 8 12
o cualquier otra secuencia en la que estés interesado.
Referencias
- J. H. Conway, and H. S. M. Coxeter. "Triangulated polygons and frieze patterns." Math. Gaz., 57(1973): 87-94, 175-183; MR 57, no. 1254-5.
- Martin Gardner. Mathematical Magic Show. Math. Assoc. Amer., 1990; Chapter 4, Factorials.
- Martin Gardner. Mathematical Circus. Math. Assoc. Amer., Spectrum Series, 1992; Chapter 13, Fibonacci and Lucas Numbers; Chapters 15, Pascal Triangle.
- Calvin T. Long. "On the Moessner theorem on integral powers." Amer. Math. Monthly, 73(1966): 846-851 (and papers of O. Perron, I. Paasche, and H. Salié quoted there).
- Calvin T. Long. "Strike it out—add it up." Math. Mag., 66(1982): 273-277.
- Yosho Mikami. The Development of Mathematics in China and Japan, 1913.
- Alfred Moessner. "Eine Bemerkung über die Potenzen der natürlichen Zahlen." S.-B. Math.-Nat. Kl. Bayer. Akad. Wiss., 1951, 29(1952); MR 14, 353b.
- Ivan Paasche. "Ein neuer Beweis des Moessnerschen Satzes." S.-B. Math.-Nat. Kl. Bayer. Akad. Wiss., 1952(1953): 1-5; MR 14, 8469.
- Ivan Paasche. "Ein zahlentheoretische-logarithmischer 'Rechensatz'." Math. Naturwiss. Unterr., 6(1953/54): 26-28.
- Ivan Paasche. "Beweis des Moessnerschen Satzes mittels linearer Kombinationen." Arch. Math., 6(1955): 194-199; MR 17, 237d.
- Paasche, Ivan. "Eine Verallgemeinerung des Moessnerschen Satzes." Compos. Math., 12(1956): 263-270.
- Joe Roberts. Lucifer's Legacy. Math. Assoc. of America, Spectrum series, 1992.
- N. J. A. Sloane and S. Plouffe. The Encyclopedia of Integer Sequences. Academic Press, New York, 1995.
Familias Famosas de Números
Muchas familias de números surgen una y otra vez en diferentes problemas matemáticos. A menudo, han recibido nombres en honor a los matemáticos que los investigaron. En este capítulo conoceremos los números de Bell y Stirling, Ramanujan, Catalan, Bernoulli y Euler, Fibonacci y Lucas.
Números de Bell y Números de Stirling
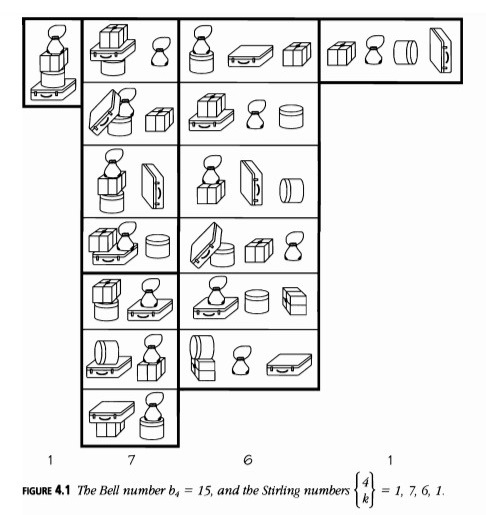
Muchos de estos números surgen al contar las diferentes formas de agrupar n objetos. ¿De cuántas formas se pueden agrupar n objetos en grupos? Si tus objetos son claramente distinguibles, la respuesta se llama usualmente número de Bell, en honor a Eric Temple Bell, conocido como matemático, historiador de las matemáticas y autor de varias historias detectivescas bajo el nombre de John Taine.
La Figura 4.1 muestra todas las formas de agrupar 4 piezas de equipaje y demuestra que el cuarto número de Bell, b4, es 15. El número de agrupamientos de n cosas distintas en exactamente k grupos se llama número de conjunto de Stirling, {n \choose k}, tradicionalmente conocido como el número de Stirling del segundo tipo.
Las cuatro columnas de la Figura 4.1 muestran que:
\[ \left\{ \begin{array}{c} 4 \\ 1 \end{array} \right\} = 1, \quad \left\{ \begin{array}{c} 4 \\ 2 \end{array} \right\} = 7, \quad \left\{ \begin{array}{c} 4 \\ 3 \end{array} \right\} = 6, \quad \left\{ \begin{array}{c} 4 \\ 4 \end{array} \right\} = 1. \]
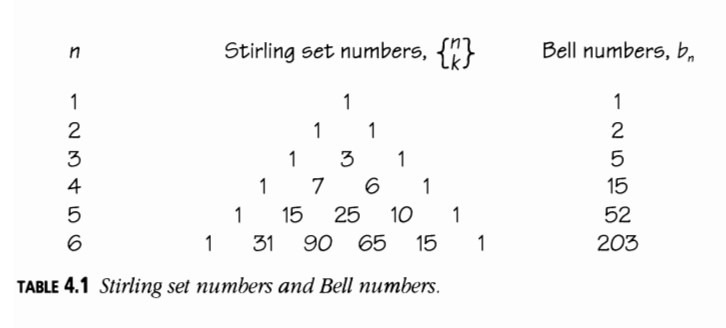
Aquí hay algunos números de conjunto de Stirling adicionales y números de Bell:
El n-ésimo número de Bell, \( b_n \), es la suma de los números de conjunto de Stirling en cada fila:
\[ b_n = \left\{ \begin{array}{c} n \\ 1 \end{array} \right\} + \left\{ \begin{array}{c} n \\ 2 \end{array} \right\} + \cdots + \left\{ \begin{array}{c} n \\ n \end{array} \right\}, \]
y es el número total de formas de organizar \( n \) objetos en grupos. Los números de ciclo de Stirling, \( \left[ \begin{array}{c} n \\ k \end{array} \right] \) (tradicionalmente llamados números de Stirling del primer tipo) cuentan las permutaciones de \( n \) objetos que tienen exactamente \( k \) ciclos. Por ejemplo, las 6 permutaciones de 3 objetos se clasifican como:
- 1 ciclo: (123), (132)
- 2 ciclos: (12)(3), (13)(2), (23)(1)
- 3 ciclos: (1)(2)(3)
y cumplen:
\[ \left[ \begin{array}{c} n \\ 1 \end{array} \right] + \left[ \begin{array}{c} n \\ 2 \end{array} \right] + \cdots + \left[ \begin{array}{c} n \\ n \end{array} \right] = n!. \]
Los triángulos en las Tablas 4.1 y 4.2 se calculan mediante variantes de la regla del triángulo de Pascal:
\[ \binom{n+1}{k} = \binom{n}{k} + \binom{n}{k-1}, \]
\[ \left\{ \begin{array}{c} n+1 \\ k \end{array} \right\} = k \left\{ \begin{array}{c} n \\ k \end{array} \right\} + \left\{ \begin{array}{c} n \\ k-1 \end{array} \right\}, \]
y
\[ \left[ \begin{array}{c} n+1 \\ k \end{array} \right] = n \left[ \begin{array}{c} n \\ k \end{array} \right] + \left[ \begin{array}{c} n \\ k-1 \end{array} \right]. \]
Algebraicamente, \( \left\{ \begin{array}{c} n \\ k \end{array} \right\} \) y \( \left[ \begin{array}{c} n \\ k \end{array} \right\} \) son los coeficientes de \( x^n \) y \( x^k \), respectivamente, en \( 1 / (1 - x)(1 - 2x) \cdots (1 - kx) \) y \( (1 + x)(1 + 2x) \cdots (1 + nx) \).
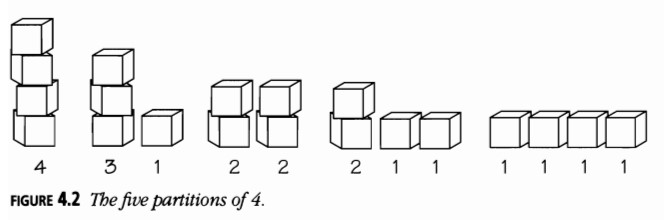
Partición y Composición de Números; Números de Ramanujan
Si tus \( n \) objetos son indistinguibles, entonces el número de formas de agruparlos se llama número de partición, \( p(n) \). La Figura 4.2 muestra que \( p(4) = 5 \) (las cinco áreas de la Figura 4.1).

No hay una fórmula exacta simple para \( p(n) \), pero hay una fórmula aproximada notable conjeturada por el famoso matemático indio, Srinivasa Ramanujan:
\[ p(n) \approx \frac{1}{4n\sqrt{3}} e^{\pi \sqrt{\frac{2n}{3}}}. \]
Esto fue probado más tarde por Hardy y Ramanujan y modificado posteriormente por Rademacher a una fórmula exacta:
\[ p(n) = \frac{1}{\pi\sqrt{2}} \sum_{k=1}^\infty A_k(n)k^{-1/2} \frac{d}{dx}\left[\sinh\left(\frac{\pi}{k}\sqrt{\frac{2}{3}}(x - \frac{1}{24})\right)\right]_{x=n}, \]
donde
\[ A_k(n) = \sum_{0 \leq h < k, \, \text{mcd}(h,k) = 1} \omega_k e^{-2\pi i nh / k}, \]
con \( \omega_k \) una cierta raíz 24ª de la unidad.
En el conteo de particiones, no nos importa el orden de las partes. Si consideramos el orden, la respuesta es mucho más simple. Hay exactamente \( 2^{n-1} \) particiones ordenadas (o composiciones, como MacMahon las llamó) de \( n \).
Quizás la fórmula más extraña para los números de partición es el método de Euler utilizando números pentagonales:
\[ p(n) - p(n-1) - p(n-2) + p(n-5) + p(n-7) - p(n-12) \ldots = 0. \]
Un Paquete de Problemas
Orpheus con su lira hizo que los árboles
Y las montañas se inclinaran...
En las próximas páginas describiremos muchos problemas que tienen la misma respuesta, ¡y luego explicaremos por qué la respuesta es siempre la misma!
Patrones de Frisos
¿Cuántas diagonales diferentes se pueden colocar en un patrón de friso con \( n+1 \) filas? Las respuestas para \( n = 1, 2, 3 \) son 1, 2, 5, respectivamente (Figura 4.3).

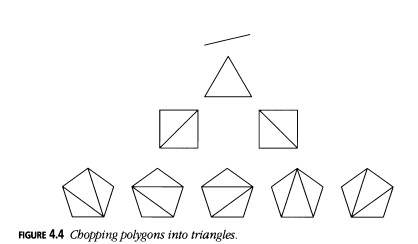
Dividiendo Polígonos en Triángulos
¿Cuántas formas hay de dividir un polígono de \( (n+2) \)-lados dado en \( n \) triángulos? (Figura 4.4)
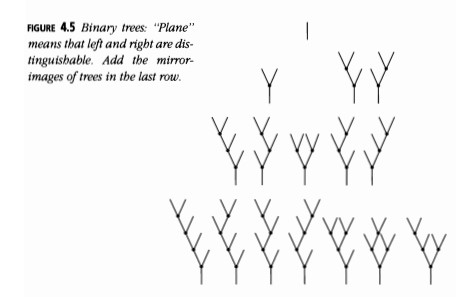
Árboles Binarios
¿Cuántos árboles binarios planos enraizados existen con \( n \) nodos internos? (Figura 4.5)
Evaluando Exponentes Escalonados
¿Cuántos valores puedes esperar de un exponente escalonado \( n \)-ple? (Figura 4.6)
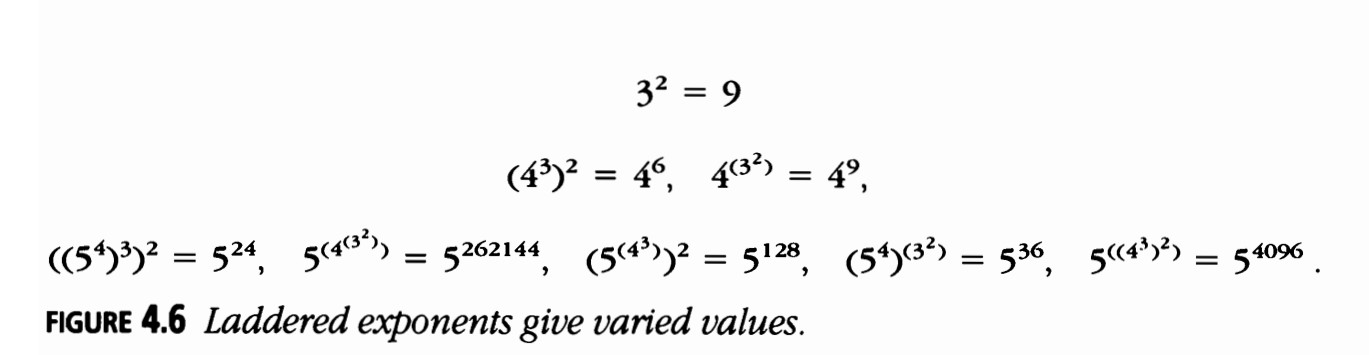
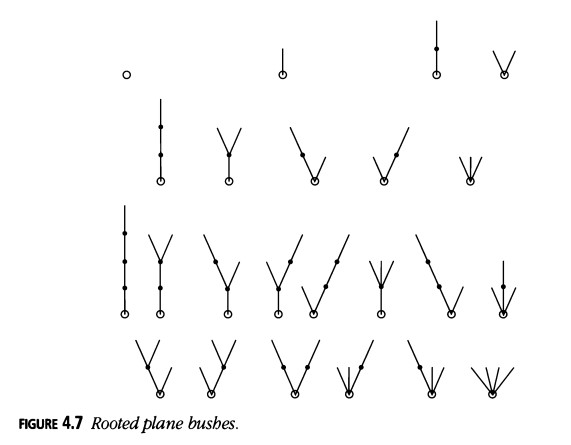
Arbustos Planos Enraizados
¿Cuántos arbustos planos enraizados existen con \( n \) bordes? (Figura 4.7)
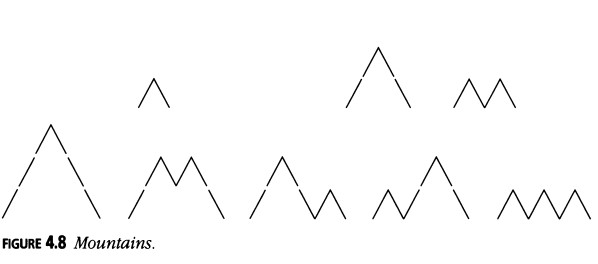
Montañas
¿Cuántas montañas puedes dibujar con \( n \) trazos hacia arriba y \( n \) trazos hacia abajo? (Figura 4.8)
Paréntesis
¿De cuántas maneras puedes disponer \( n \) pares de paréntesis? (Figura 4.9)
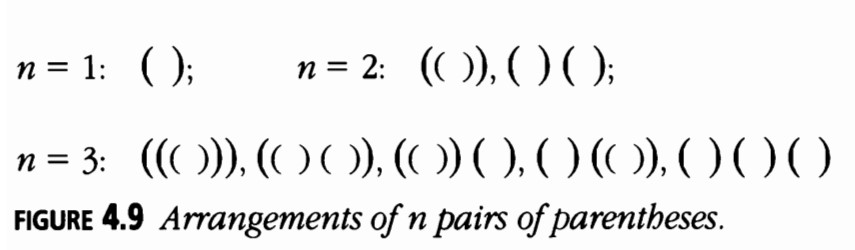
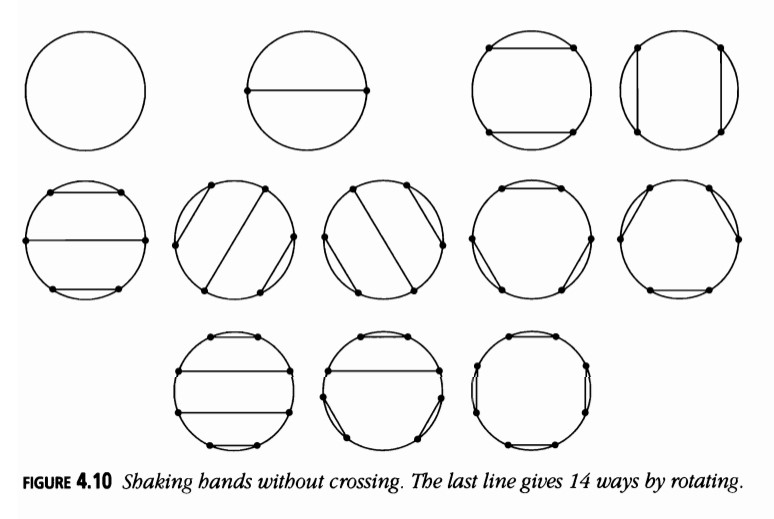
Manos Cruzadas en la Mesa
¿Cuántos apretones de manos sin cruces son posibles con \( n \) pares de personas? (Figura 4.10)
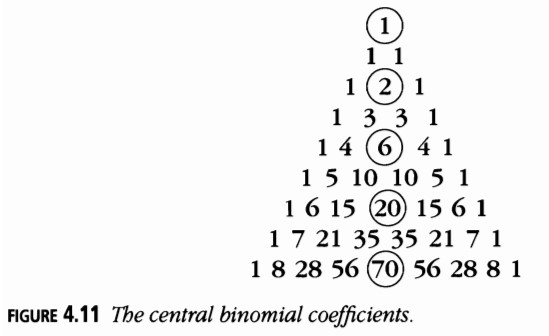
Números de Catalan
Observa los números centrales en el triángulo de Pascal (Figura 4.11):
\( 1, \ 2, \ 6, \ 20, \ 70, \ 252, \ 924, \ 3432, \ 12870, \ 48620, \dots \)
Parece que podemos dividirlos por:
\( 1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8, \ 9, \ 10, \dots \)
para obtener la siguiente secuencia de números enteros:
\( 1, \ 1, \ 2, \ 5, \ 14, \ 42, \ 132, \ 429, \ 1430, \ 4862, \dots \)
Un número central típico es el coeficiente binomial, \( \binom{2n}{n} \), por lo que nuestra conjetura es:
\[ c_n = \frac{1}{n+1} \binom{2n}{n} = \frac{2n!}{n!(n+1)!} = \frac{1}{2n+1} \binom{2n+1}{n}. \]
Estos números se llaman números de Catalan. Ahora mostraremos que todos los problemas anteriores tienen la misma respuesta.
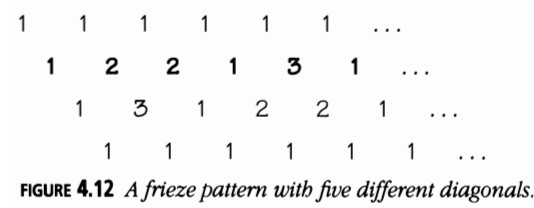
Frisos y Polígonos
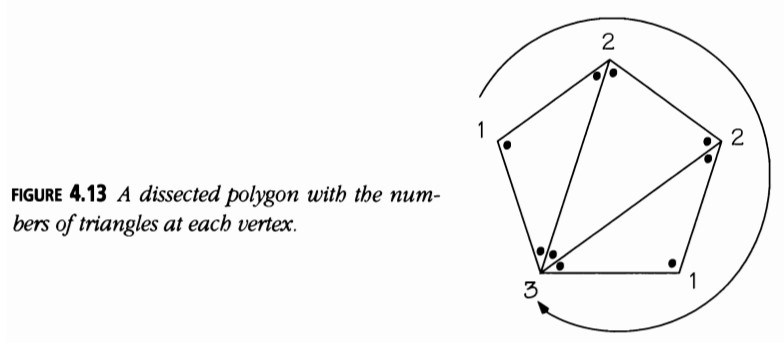
La correspondencia entre frisos y polígonos es bastante fácil de describir. El patrón de friso (Figura 4.12) corresponde al polígono etiquetado en diagonales de triángulo (Figura 4.13) porque la nueva fila debajo de la fila superior de unos en la Figura 4.12 indica el número de triángulos en los vértices del polígono.
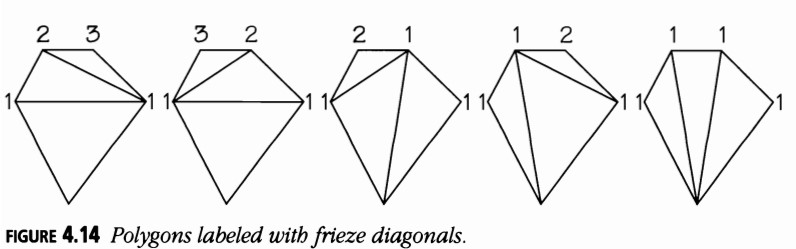
Alternativamente, en la Figura 4.14, deja sin etiquetar el vértice inferior izquierdo y etiqueta todos los vértices conectados a él con unos. Luego etiqueta otros vértices de manera que el número en el último vértice de cualquier triángulo sea la suma de los otros dos. Lee alrededor de las etiquetas y obtendrás las cinco diagonales diferentes del friso de la Figura 4.12.
Un patrón más complicado y el polígono correspondiente aparecieron en el Capítulo 3. Conway y Coxeter han dado una explicación completa de por qué esto funciona.
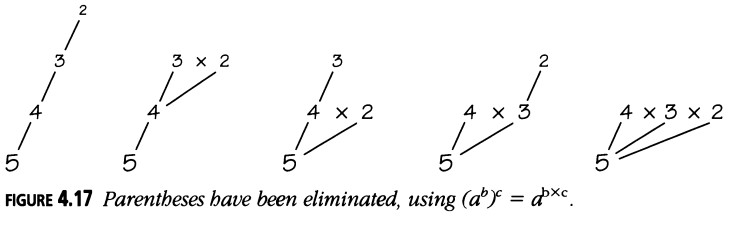
Árboles y Exponenciaciones
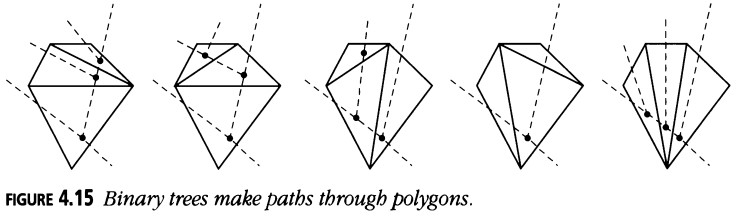
La Figura 4.15 muestra cómo los polígonos divididos corresponden a árboles binarios planos.
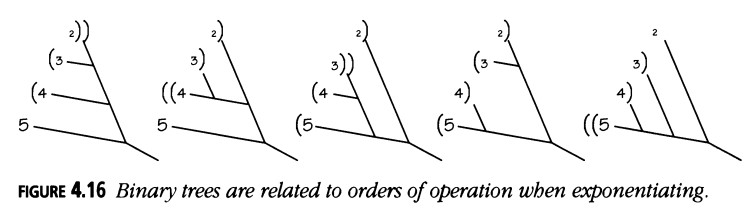
La Figura 4.16 relaciona los árboles binarios con expresiones exponenciales, y la Figura 4.17 asocia estas últimas con arbustos.
Exponenciales y Arbustos
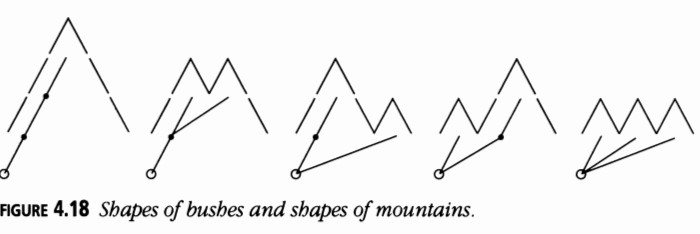
Montañas y Paréntesis
La Figura 4.18 vincula los arbustos con montañas; la Figura 4.19 vincula las montañas a nidos de paréntesis; y la Figura 4.20 conecta estos con apretones de manos.
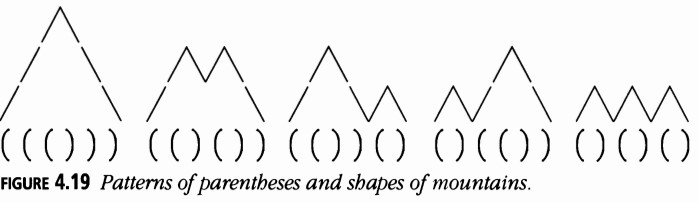
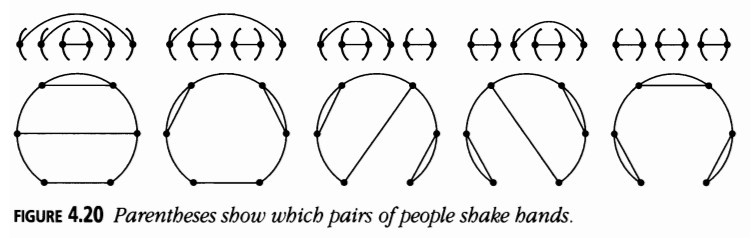
Paréntesis y Apretones de Manos
Todos estos objetos variados (y de hecho muchos más) son contados por los mismos números. ¡Para ver que son los números de Catalan, quizás sea más fácil contar las montañas!
Montañas y números de Catalan
Si añadimos un trazo ascendente extra, hay \(7! / 4!3! = 35\) secuencias de 4 trazos ascendentes y 3 descendentes, pero si continuamos estos patrones periódicamente (Figura 4.21), obtenemos solo 5 diferentes secuencias infinitas, que se dividen naturalmente en las líneas discontinuas para revelar las 5 diferentes montañas con 3 trazos ascendentes y 3 descendentes.
En general, las montañas con \(n\) trazos ascendentes y \(n\) descendentes corresponden a: \[ \frac{1}{2n+1} \binom{2n+1}{n} \]

Este es uno de los tres fórmulas que dimos para \(c_n\), el n-ésimo número de Catalan.
Estamos seguros de que ya has visto suficiente sobre los números de Catalan, así que pasaremos a un nuevo tema.
La fórmula de Faulhaber
Ya hemos visto las fórmulas para las sumas de números hasta \(n\), y de sus cuadrados y cubos, en el Capítulo 2: \[ 1^0 + 2^0 + \ldots + n^0 = n, \] \[ 1^1 + 2^1 + \ldots + n^1 = \frac{1}{2} [n^2 + n], \] \[ 1^2 + 2^2 + \ldots + n^2 = \frac{1}{3} [n^3 + \frac{3}{2}n^2 + \frac{1}{2}n], \] \[ 1^3 + 2^3 + \ldots + n^3 = \frac{1}{4}[n^4 + 2n^3 + n^2]. \]
Johann Faulhaber, conocido en su tiempo como el Gran Aritmético de Ulm pero ahora casi olvidado, trabajó en la fórmula para las sumas de potencias mayores en su Academiae Algebrae (1631): \[ 1^k + 2^k + \ldots + n^k = \frac{1}{k}\left[n^k + \binom{k}{1}n^{k-1} \times \frac{1}{2} + \binom{k}{2}n^{k-2} \times \frac{1}{6} + \binom{k}{3}n^{k-3} \times 0 + \ldots\right]. \]
Observa que la expresión entre corchetes es exactamente como la fórmula para el teorema binomial, excepto que no hay término constante y los otros términos se multiplican por ciertas constantes: \[ 1 \quad \frac{1}{2} \quad \frac{1}{6} \quad 0 \quad -\frac{1}{30} \quad 0 \quad -\frac{1}{42} \quad 0 \quad 0 \quad \frac{5}{66} \quad 0 \quad \ldots \]
Números de Bernoulli
Estas constantes en la fórmula de Faulhaber se conocen como los números de Bernoulli, ya que se discuten intensamente en la obra póstuma de Jacob (James) Bernoulli, Ars Conjectandi (1713), aunque Bernoulli da el crédito completo a Faulhaber.
Para recordarnos la conexión con el teorema binomial, usaremos los nombres:
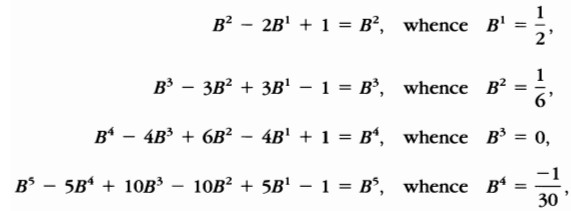
Al igual que si los números de Bernoulli fueran potencias (lo cual, por supuesto, no lo son).
La fórmula de Faulhaber puede escribirse formalmente como:
\( 1^k + 2^k + \cdots + n^k = \frac{(n + B^k)^k - B^k}{k}. \)
Las expresiones dentro de las "comillas" deben interpretarse como una suma de términos, donde cada uno es una potencia de \( B \) multiplicada por algún número, y las potencias de \( B \) deben entenderse como números de Bernoulli.
Jacob Bernoulli se jactaba de haber encontrado la suma de las potencias décimas de los primeros mil enteros intra semiquadrantem horae (¡en 7½ minutos!) Ahora que conoces la fórmula de Faulhaber, puedes verificar esto en menos tiempo:
\( "(x + B)^{11} - B^{11}" \div 11 = \frac{1}{11}(x^{11} + 11B x^{10} + 55B^2 x^9 + 330B^3 x^7 + 462B^5 x^5 + 165B^8 x^3 + 11B^{10}x) \),
con \( x = 1000 \) y \( B^1 = \frac{1}{2}, B^2 = \frac{1}{6}, B^4 = -\frac{1}{30}, B^6 = \frac{1}{42}, B^8 = -\frac{1}{30}, B^{10} = \frac{5}{66} \), tienes:

Cómo encuentras los números de Bernoulli? Puedes definirlos y computarlos mediante las ecuaciones:
\( B^2 - 2B^1 + 1 = B^2, \text{ donde } B^1 = \frac{1}{2}; \)
\( B^3 - 3B^2 + 3B^1 - 1 = B^3, \text{ donde } B^2 = \frac{1}{6}; \)
\( B^4 - 4B^3 + 6B^2 - 4B^1 + 1 = B^4, \text{ donde } B^3 = 0; \)
\( B^5 - 5B^4 + 10B^3 - 10B^2 + 5B^1 - 1 = B^5, \text{ donde } B^4 = -\frac{1}{30}; \)
y, en general:
\( "(B - 1)^k = B^k" \quad (\text{para } k \neq 1) \).
Así, \( B^{k-1} \) puede calcularse si ya conoces \( B^1, B^2, \ldots, B^{k-2} \). Por otro lado, \( B^0 = (B - 1)^1 \) y \( B^1 \) no son iguales. De hecho:
\( (B - 1)^1 = B^1 - 1 = -\frac{1}{2}, \text{ mientras que } B^1 = \frac{1}{2}. \)
Restando ambas expresiones, obtenemos:
“(100 + \( B^k \)) − (99 + \( B^k \))” = \( k \cdot 100^{k-1} \).
Ahora sumamos un centenar de tales ecuaciones y cancelamos muchos términos:
\[ “(100 + B^k) − (99 + B^k)” = k \cdot 100^{k-1} \\ “(99 + B^k) − (98 + B^k)” = k \cdot 99^{k-1} \\ \cdots \\ “(2 + B^k) − (1 + B^k)” = k \cdot 2^{k-1} \\ “(1 + B^k) − B^k” = k \cdot 1^{k-1} \]
que es la fórmula de Faulhaber.
EULER NUMBERS AND ZIGZAG ARRANGEMENTS
¿Cuál es el número, \( Z_n \), de arreglos en zigzag de 1, 2, ..., \( n \), es decir, arreglos en los que los números alternativamente suben y luego bajan? La Tabla 4.4 muestra los primeros valores de esto.

Los puntos y comas separan los arreglos según su último número, \( r \). El número de arreglos en zigzag de 1, 2, ..., \( n \) con último número \( r \) es la entrada \( r \)-ésima en la fila \( n \)-ésima del triángulo en zigzag.

El triángulo zigzag se calcula en el método "boustrophedon" insinuado por las flechas. Cada fila ahora se encuentra sumando alternadamente los números de la fila anterior, primero de izquierda a derecha y luego de derecha a izquierda.
La frontera izquierda contiene los números zigzag, \( Z_{2n} \), que tradicionalmente se llaman números de Euler; también se conocen como números secantes en vista de la fórmula:
\[ \sec x = 1 + \frac{1}{2!} + \frac{5 \cdot x^4}{4!} + \frac{61 \cdot x^6}{6!} + \frac{1385 \cdot x^8}{8!} + \ldots \]
El borde derecho contiene los números zag o números tangentes, Z2n+1, ya que:
tan x = x / 1! + 2·x³ / 3! + 16·x⁵ / 5! + 272·x⁷ / 7! + 7936·x⁹ / 9! + ...
El número total de arreglos de 1, 2, ..., n en los que hay exactamente k incrementos también ha sido nombrado en honor a Euler, pero para distinguirlo, lo llamamos el número euleriano, A(n, k):
A(n, k) = Σj=0k (-1)j (n + 1)Cj(k - j)n.
Números de Fibonacci
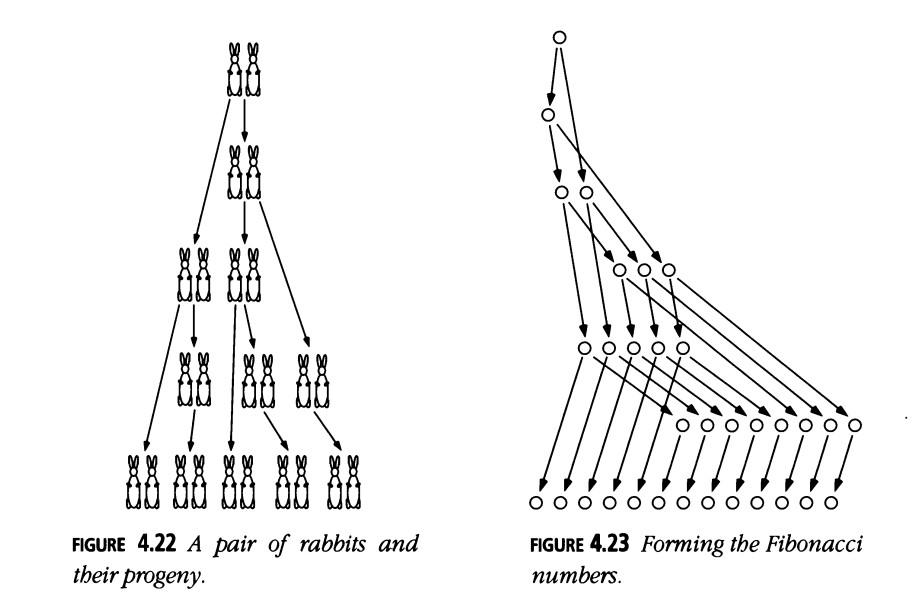
Leonardo de Pisa (ca. 1200) se preguntó cuántos pares de conejos se producirían en la generación n-ésima, comenzando con un solo par y suponiendo que cualquier par de conejos de una generación produce un par de conejos para la próxima generación y uno para la generación siguiente, y luego mueren.
Si hay fn pares de conejos en la generación n, entonces:
f1 = 1 (la pareja original), f2 = 1 (su progenie inmediata), fn+2 = fn + fn+1,
ya que obtenemos un par en la generación n + 2 por cada par en la generación n o en la generación n + 1 (ver Figuras 4.22 y 4.23).
f0 = 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 ...
Estos son los llamados números de Fibonacci, ya que el padre de Leonardo era apodado Bonacci, y así Leonardo fue llamado Fibonacci (filio Bonacci = "hijo del hombre de buen carácter"). Los números de Fibonacci surgen de tantas maneras que es casi increíble: sus manifestaciones son tan numerosas como los conejos de Leonardo. Incluso existe una publicación matemática periódica, el Fibonacci Quarterly, dedicada enteramente al tema. Solo mencionaremos algunas de las propiedades más notables.
Los números de Lucas, ln
l0 = 2 1 3 4 7 11 18 29 47 76 123 199 322 521 843 1364 ...
(definidos por la misma regla, pero con un comienzo diferente) están relacionados con los números de Fibonacci de muchas maneras:
f2n = fnln, f0 + f1 + ... + fn = fn+2 - 1, ln = fn-1 + fn+1, 2fm+n = fmln + fnlm.
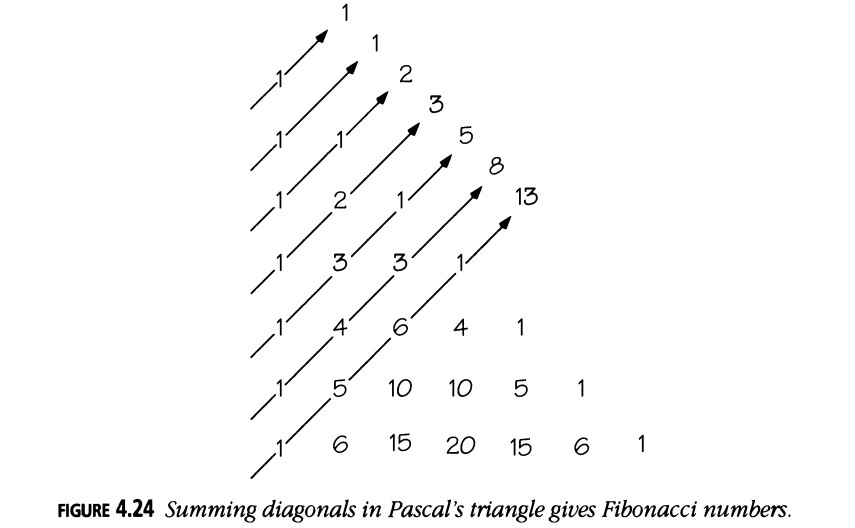
Esta última relación, notada por Lucas, muestra que se pueden leer los números de Fibonacci del triángulo de Pascal (Figura 4.24).
Kepler señaló que las proporciones de números consecutivos de Fibonacci se acercan a 1.618... El límite exacto se llama el número áureo:
τ = (1 + √5) / 2 = 1.6180339887498948482...
... lo cual era conocido por los griegos. Las proporciones de números consecutivos de Lucas tienden al mismo límite, mientras que la relación, ln/fn, entre los números correspondientes de Lucas y Fibonacci, tiende a √5. De hecho, existen fórmulas para fn y ln, en términos del número áureo, que daremos en el Capítulo 7.
El problema de los conejos de Leonardo, por supuesto, no es del todo realista. Sin embargo, los números de Fibonacci sí aparecen en la naturaleza. Puedes encontrarlos en piñas, cactus, conos de pino y girasoles: también controlan la disposición de las hojas de casi todas las plantas.
Filotaxis
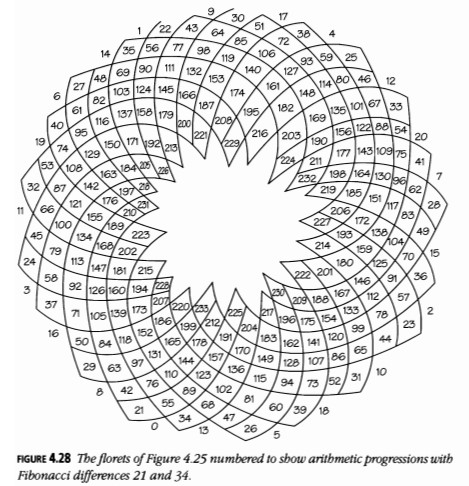
El término botánico para la disposición de las hojas es filotaxis. Observa los floretes en el capítulo del girasol en la Figura 4.25. Parecen formar dos sistemas de espirales, que irradian desde el centro. Aunque parece simétrico, el número de espirales en el sentido de las agujas del reloj y en sentido contrario no son iguales. Si los cuentas con cuidado, encontrarás 55 espirales en sentido horario y 34 en sentido antihorario.

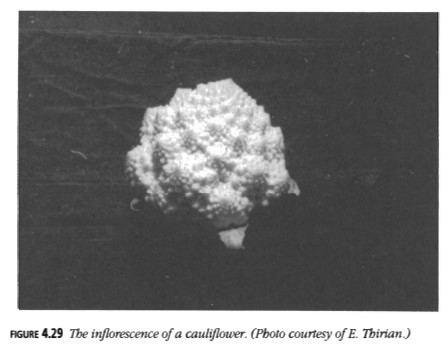
Las piñas en la Figura 4.26 y la margarita en la Figura 4.27 exhiben un fenómeno similar. En la Figura 4.28, que es un trazado de la Figura 4.27, enfatizamos las 21 espirales que van en una dirección y las 34 que van en la otra al numerar los pétalos. Puedes ver tales espirales en muchas otras plantas, como coliflores (Figura 4.29), conos de pino y ciertos tipos de cactus. Por lo general, hay dos sistemas de floretes, semillas, ramas, pétalos o lo que sea, que van en direcciones opuestas, y los números de espirales en estos sistemas son números consecutivos de Fibonacci. ¿Por qué es esto así?
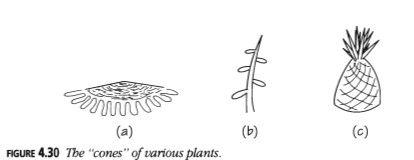
Describiremos lo que ocurre en una etapa temprana de la vida de la planta. Consideramos la punta de la planta como un cono y observamos la llegada inicial de "brotes" en este cono. El cono puede ser muy plano, como en el girasol (Figura 4.30(a)), o puntiagudo, como en el tallo (Figura 4.30(b)), o estar en algún punto intermedio, como en la piña de la Figura 4.30(c).


Estos brotes pueden convertirse en semillas en una cápsula de semilla, ramas en una rama, pétalos de una flor, y así sucesivamente. Sin embargo, en esta etapa de su vida, un brote inhibe o repele a los demás. Esto puede deberse a que están apretados y físicamente se empujan entre sí, o tal vez estén compitiendo por nutrientes esenciales, o tal vez estén secretando deliberadamente alguna sustancia inhibidora.
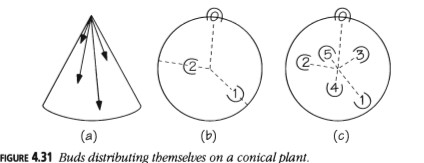
Consideramos el crecimiento de nuestra planta como ocurriendo en la punta del cono. Dado que la punta avanza continuamente debido al nuevo crecimiento, una porción determinada de la planta se mueve constantemente hacia abajo y hacia afuera con respecto a la punta (Figura 4.31(a)).
Oye, Brote, ¿A Dónde Crees Que Vas?
Numeraremos los brotes 0, 1, 2, ..., en el orden de su aparición. En la vista plana de la Figura 4.31(b), hemos colocado el brote número 0 en la posición de las 12 en punto y, como nació primero, ya ha llegado al perímetro. Los brotes 0 y 1 separan el cono en sectores más grandes y más pequeños. El brote 2 encuentra más fácil existir en el sector más grande, forzando al 3 a entrar en el más pequeño. ¿Dónde estarán estos brotes dentro de los sectores? Como el número 1 es más nuevo y más cercano a la punta que el número 0, probablemente sea más inhibidor, por lo que los números 2 y 3 estarán un poco más cerca de 0 que de 1. Los hemos colocado aproximadamente a las 9 en punto y a las 2 en punto en las Figuras 4.31(b) y (c). En esta etapa tenemos cuatro sectores, el mayor de los cuales está entre los brotes 1 y 2. Esperamos que el brote 4 nazca en este sector, ligeramente más cerca de 1, ya que es más reciente.
Este proceso puede parecer un poco tosco, pero en realidad es extremadamente estable. Supongamos, por ejemplo, que el brote número 1 nació más o menos exactamente opuesto al número 0, dejando dos sectores iguales abiertos para el número 2. El número 2 elegiría al azar uno de estos y, al crecer, se empujaría lejos del 0 y 1 (pero ligeramente más lejos del 1) y así agrandaría su propio sector. Fenómenos similares ocurren en etapas posteriores del proceso. El lector también debe comprender que la acción tiene lugar en una etapa muy temprana del desarrollo, de modo que probablemente se encuentre en un entorno uniforme en todas partes, tal vez solo a unos pocos milímetros de distancia.
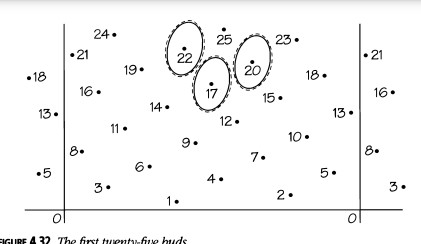
La Figura 4.32 muestra lo que sucede cuando muchos brotes se han desarrollado. Esta vez hemos tomado una planta idealizada en la que el cono es casi cilíndrico y hemos desenrollado el cilindro. Por supuesto, una planta real no tendrá los brotes exactamente en los "lugares correctos", pero tampoco pueden estar muy lejos. Los elipses punteadas en la Figura 4.32 muestran cómo las esferas de influencia de los brotes 17, 20 y 22 dejan un agujero listo para el brote número 25. No nacerá demasiado lejos del centro de este agujero, y aun si está un poco fuera de posición, a medida que crezca se abrirá camino hacia el lugar correcto. Una vez que se establece el proceso, es muy raro que pierda su forma.
En la versión perfecta del proceso, cada nuevo brote avanza con el mismo ángulo, siendo este el que divide un giro completo en una sección áurea. En nuestras figuras, este ángulo es 0.618 de una revolución en sentido antihorario, o 0.382 de una revolución en sentido horario.
¿Cuántas espirales hay? Estas espirales son muy subjetivas, dependiendo del observador. Tiendes a conectar brotes vecinos en una cadena. Así, en la Figura 4.32, probablemente vincules mentalmente los brotes en líneas con una diferencia de 3 que suben hacia la derecha, y líneas con diferencia de 5 que suben hacia la izquierda.
Por otro lado, si entrecierras los ojos para ver la figura desde abajo, puede resultarte más fácil organizar los brotes en líneas con diferencias de 8 o incluso de 13. Los números de Fibonacci sucesivos surgen como múltiplos de este ángulo básico que se acercan más a los números enteros de revoluciones. Los números de Fibonacci particulares que notas dependen de cuánto está comprimido el eje vertical en comparación con el horizontal. Las Figuras 4.33 y 4.34 son simplemente la Figura 4.32 con el eje vertical más comprimido, y divididas en dominios asignando cada punto a su brote más cercano.
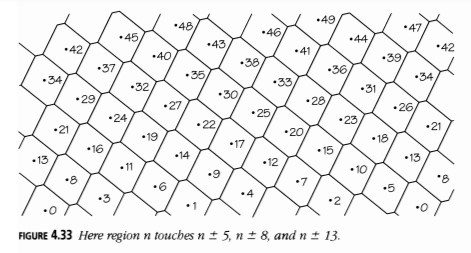
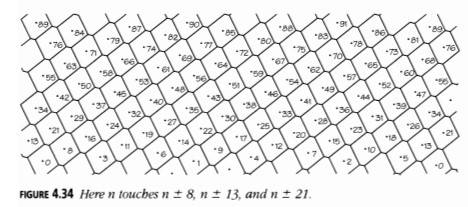
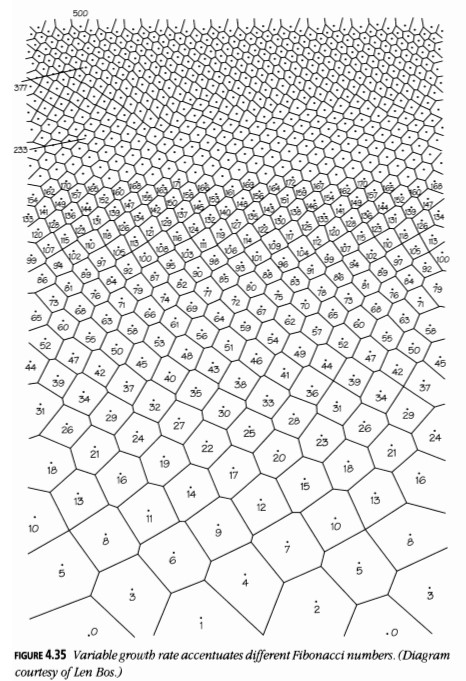
En la Figura 4.32, los números 3, 5 y 8 son los más evidentes; en la Figura 4.33, con la escala multiplicada por un medio, 5 y 8 son más notorios; en la Figura 4.34, con la escala reducida a un quinto, 8, 13 (y 21) son los más obvios. En la parte inferior de la Figura 4.35, los números 3, 5 y 8 son prominentes; en la parte superior, los números 13 y 21 comienzan a predominar.
Antes de la próxima vez que comas una piña, intenta encontrar los números correctos.
El patrón es generalmente más fácil de seguir a mitad de camino hacia arriba, pero con un poco de cuidado puedes trabajar hacia la base e incluso identificar el número 0.
Las hojas en los tallos de las plantas exhiben remanentes de este proceso. Los brotes de hojas embrionarias en tales casos estaban originalmente apilados bastante apretados alrededor del tallo, como en nuestras figuras. En una fase posterior de crecimiento, el tallo se alarga, de modo que todo lo que queda del arreglo original es una tendencia de cada hoja a girar alrededor de 0.382 (o aproximadamente 2/5) de una revolución con respecto a su predecesora.
Los pétalos de una rosa exhiben el mismo fenómeno en la forma en que se superponen a sus predecesores, pero usualmente están tan apretados que la estructura es difícil de ver sin diseccionarlos. La Figura 4.36 muestra una flor en la que hemos numerado los pétalos individualmente.

Incluso podemos especular que el número exacto (cuando es pequeño) de pétalos en una flor podría determinarse mediante tal mecanismo. La siguiente tabla muestra en fracciones de una revolución el ángulo que define la posición del número de pétalo n (esto es, solo la parte fraccional de nτ) y también el ángulo más pequeño entre este pétalo y cualquiera de sus predecesores. Si este último fuera el único parámetro relevante, se estimaría la probabilidad de la aparición del número de pétalo n.
| Número de pétalo | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Posición angular | 0 | 0.618 | 0.236 | 0.854 | 0.472 | 0.090 | 0.708 | 0.326 | 0.944 |
| Ángulo más pequeño | — | 0.382 | 0.236 | 0.146 | 0.146 | 0.090 | 0.090 | 0.090 | 0.056 |
Los ángulos de posición son solo las partes fraccionarias de múltiplos sucesivos
0, 1.618..., 3.236..., 4.854...
del número áureo
Con esta visión, verá que el quinto pétalo (número 4) encuentra las cosas con la misma facilidad (0.146) que su predecesor, mientras que el sexto y los posteriores tienen un tiempo sustancialmente más difícil (0.090). Sin necesidad de contar, pero simplemente estableciendo un nivel dado de inhibición, una flor puede arreglarse para que el número total de pétalos sea un pequeño número de Fibonacci, pero no otro número.
No es tan fácil controlar las cosas para obtener un número mayor de Fibonacci exactamente, ya que la influencia del pétalo número 0 se vuelve rápidamente menos perceptible. De hecho, cuando una flor tiene un gran número de pétalos, el número exacto de pétalos generalmente depende del espécimen particular.
El lector debería tener cuidado de no forzar demasiado esta teoría, porque las plantas usan muchos otros mecanismos en su desarrollo. Algunas emiten pares de hojas simultáneamente en lados opuestos del tallo. Los pares sucesivos pueden luego rotar en 0.191 (la mitad de 0.382) de una revolución, pero son igual de propensos a rotar en un ángulo recto. Muchas flores tienen exactamente seis pétalos. Por ejemplo, en estas, suele ser el caso de que los pétalos están organizados como dos generaciones de tres pétalos cada una. Este efecto se muestra muy claramente en un narciso; de hecho, los primeros tres de sus "pétalos" son sépalos en lugar de pétalos.
Ocasionalmente, uno ve piñas de pino en las que el número de espirales son los dobles de números de Fibonacci. Presumiblemente, esto ocurrió porque los brotes 0 y 1 emergieron casi simultáneamente en lados opuestos y el proceso subsiguiente fue sesgado.
La próxima vez que coma una cabeza de coliflor, note que no solo tiene números de Fibonacci de espirales de floretes, sino que a menudo tiene espirales de subflósculos. Y en su caminata a través del bosque, fíjese en...
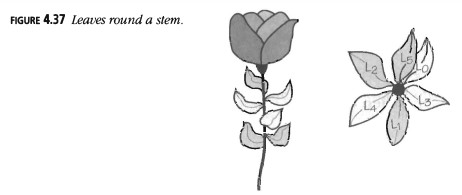
...el tallo de una planta. Si dos hojas parecen estar una sobre la otra (Figura 4.37), probablemente están separadas por un número de Fibonacci.
La disposición de las ramas más grandes en un árbol es a menudo más aleatoria, pero hay algunas especies de árboles de montaña en las que la organización de Fibonacci puede verse en toda la estructura, incluso en las raíces, si excava hasta ellas.
Referencias
- V. I. Arnold. Bernoulli-Euler updown numbers associated with function singularities, their combinatorics and arithmetics, Duke Math. J. 63(1991): 537–555.
- V. I. Arnold. Snake calculus and combinatorics of Bernoulli, Euler and Springer numbers for Coxeter groups. Russian Math. Surveys 47(1992): 3–45.
- E. R. Berlekamp, J. H. Conway, and R. K. Guy. Winning Ways for your Mathematical Plays, Academic Press, 1982, 475–478, 501.
- N. G. de Bruijn & B. J. M. Morselt. A note on plane trees. J. Combin. Theory 2(1967): 27–34.
- B. L. Burrows & R. F. Talbot. Sums of powers of integers. Amer. Math. Monthly 91(1984): 394–403.
- J. H. Conway & H. S. M. Coxeter. Triangulated polygons and frieze patterns. Math. Gaz. 57(1973): 87–94, 175–184; MR 57, no. 1254–5.
- A. W. F. Edwards. A quick route to sums of powers. Amer. Math. Monthly 93(1986): 451–455.
- Antal F. Fekete. Apropos two notes on Eulerian numbers. Math. Monthly 101(1994): 771–778.
- Martin Gardner. Time Travel and other Mathematical Bewilderments, W. H. Freeman, New York, 1988, capítulo 20, Números de Catalan.
- Johann Wolfgang von Goethe. Versuch die Metamorphosa der Pflanzen zu erklären, Gotha, 1790.
- H. W. Gould. Bell & Catalan Numbers: Research Bibliography of Two Special Number Sequences, Sexta Edición, Morgantown, WV, 1985.
- Ronald L. Graham, Donald E. Knuth & Oren Patashnik. Concrete Mathematics, A Foundation for Computer Science, Addison-Wesley, Reading, MA, 1989.
- J. Karamata. Théorèmes sur la sommabilité exponentielle et d'autres sommabilités s'y rattachant. Mathematica (Cluj), 9(1935): 164–178.
- A. A. Kirillov. Variations on the triangular theme in S. G. Gindikin & E. B. Vinberg (editores). E. B. Dynkin Seminar on Lie Groups. Amer. Math. Soc., 1995.
- Donald E. Knuth. Two notes on notation. Amer. Math. Monthly 99(1992): 403–422.
- D. E. Knuth & T. J. Buckholtz. Computation of tangent, Euler and Bernoulli numbers. Math. Comput. 21(1967): 663–688.
- Mark Krusemeyer. A parenthetical note (to a paper of Richard Guy). Math. Mag. 69(1996).
- Michael J. Kuchinski. Catalan Structures and Correspondences. Tesis de Maestría, West Virginia University, 1977.
- Luo Jian-Jin. An Tu Ming, the first discoverer of the Catalan numbers. Niemenggu Daxue Xuebo 19(1988): 239–245; MR 90e:01007.
- J. Millar, N. J. A. Sloane & N. E. Young. A new operation on sequences: The boustrophedon transform, 95-09-25 preprint.
- Th. Motzkin. Relations between hypersurface cross-ratios, and a combinatorial formula for partitions of a polygon, for permanent preponderance, and for non-associative products. Bull. Amer. Math. Soc. 54(1948): 352–360; MR 9: 489–490.
- C. D. Oakley & R. J. Wisner. Flexagons. Amer. Math. Monthly 64(1957): 143–154; MR 19: 241b.
- Przemyslaw Prusinkiewicz & Aristid Lindenmayer. The Algorithmic Beauty of Plants, con James S. Hanan, F. David Fracchia, Deborah R. Fowler, Martin J. M. de Boer & Lynn Mercer, Springer-Verlag, 1990.
- H. Rademacher. On the partition function p(n). Proc. London Math. Soc. (2), 43(1937): 241–254.
- Ibrahim A. Salama & Lawrence E. Kupfer. A geometric interpretation for the Catalan numbers. Amer. Math. Monthly 93(1986): 51–52.
- A. A. Sillke. Some applications of the Catalan numbers. Math. Monthly 89(1982): 698; solución David M. Wells, 93(1986): 217–218.
- Ian Stewart. Mathematical Recreations: Daisy, Daisy, give me your answer, do. Sci. Amer. 272#1 (enero de 1995): 96–99.
- Peter Guthrie Tate. Proc. Royal Soc. Edinburgh VII (1870–71): 391–394.
- D'Arcy Wentworth Thompson. On Growth and Form, Cambridge Univ. Press, 1952.
- C. W. Wardlaw. Organization and Evolution in Plants. Longmans Green, 1965.
La Primacía de los Primos
Aunque los aritméticos han estudiado los números primos durante miles de años, hoy en día existen más problemas abiertos que nunca antes. La mayoría de los enteros positivos pueden expresarse como el producto de números más pequeños; tales productos se llaman números compuestos.
4 = 2 × 2, 6 = 2 × 3, 8 = 2 × 4, 9 = 3 × 3, 10 = 2 × 5, 12 = 3 × 4
Son ejemplos de números compuestos.
El número 1 está en una categoría única y se llama la unidad. Los números restantes, mayores que 1, pero que no son producto de números más pequeños:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, ...
Se llaman números primos. Quizás el mayor misterio sobre los números primos es que, aunque están definidos de manera simple, se comportan de forma bastante irregular.
Eratóstenes (276-194 a.C.), bibliotecario de la gran biblioteca de Alejandría, fue una de las mentes más brillantes del mundo antiguo.
Quizás su logro más notable fue la medición de la circunferencia de la Tierra en una época en que pocas personas creían que era redonda, comparando las longitudes de las sombras de mástiles al mediodía en Alejandría y en Siene (Asuán). Pero los teóricos de números siempre lo recordarán por su maravilloso tamiz para los números primos. Al igual que el granjero separa el valioso trigo de la paja inútil, Eratóstenes utilizó su tamiz para separar los preciosos primos de sus compañeros compuestos comunes. Así es como funciona:
Escribe los números en orden, colocando el 1 en un cuadro para mostrar que es la unidad.
Encierra en un círculo el primer número restante, que es el 2, y tacha cada segundo número a partir de ahí:
Encierra en un círculo el siguiente número restante, que es el 3, y tacha todos los múltiplos subsiguientes de ese número:
Si continúas de esta manera en cada etapa, encerrando el primer número restante y tachando sus múltiplos superiores, los números que encierras serán los números primos (Figura 5.1).
Muchos números se tachan más de una vez. Por ejemplo, tachamos el 6 como múltiplo de 3, aunque ya había sido tachado como múltiplo de 2. De hecho, cuando estamos manejando un número primo p, sus múltiplos por números menores que p ya habrán sido tratados, y el primero que no haya sido tratado será
p veces p = p2
Cuando tratamos con 2 y 3, dejando 5 como el próximo primo, los números restantes:
5, 7, 11, 13, 17, 19, 23
por debajo de 52 = 25 ya se sabe que son primos.
El proceso de tamizado se facilita si escribes los números en una cuadrícula...
En la Figura 5.1, hemos dibujado solo los números impares menores de 361 = 19², y las diversas líneas rectas tachan los múltiplos de 3, 5, 7, 11, 13 y 17. Por lo tanto, los números restantes son 1 y los primos impares menores de 360.
Como resultado de un esfuerzo colaborativo durante el siglo XIX, se publicaron tablas que daban los números primos y los factores de otros números para cada millón sucesivo, hasta diez millones. Este trabajo culminó en 1909 con la publicación de la tabla de factores para los primeros diez millones de Derrick Norman Lehmer. En 1914, Lehmer también publicó una lista de números primos menores de diez millones, extraída de su tabla de factores.
Todas estas tablas se calcularon utilizando el tamiz de Eratóstenes. De hecho, el papel en el que Lehmer realizó sus cálculos estaba soportado por una mesa muy larga, equipada con rodillos en cada extremo, y para los primos más pequeños, creó plantillas de papel con agujeros que le permitían marcar sus múltiplos. Algunas de estas mesas tenían entre 15 y 20 pies de largo.
Es interesante notar que el aritmético austríaco J. P. Kulik (1773–1863) pasó 20 años de su vida preparando una tabla con 100 millones de números a mano, pero nunca se publicó, y el volumen para los números del 12,642,600 al 22,852,800 se ha perdido.
El número 1 solía contarse como un número primo; aparece, por ejemplo, en la lista de números primos de D. N. Lehmer. Pero hay tantas maneras en que difiere de los verdaderos números primos apropiados que los matemáticos ahora lo colocan en su clase especial. Por ejemplo, si comenzaras el proceso de tamizado con 1, ¡tendrías que tachar todo lo demás!
Aritmética Módulo p
Números Módulo p
Cuando p es primo, los números módulo p forman un campo fructífero para la investigación.
Está claro que módulo cualquier número puedes sumar, restar o multiplicar, pero lo fascinante de los primos es que también puedes dividir. Módulo un número primo, tiene sentido hablar de fracciones.
Fracciones Módulo p
Si trabajamos módulo 7, entonces
\(2 \times 4 \equiv 1\), \(3 \times 5 \equiv 1\), y \(6 \times 6 \equiv 1\).
Por lo tanto, es bastante correcto decir que
\(\frac{1}{2} \equiv 4\), \(\frac{1}{3} \equiv 5\), \(\frac{1}{4} \equiv 2\), \(\frac{1}{5} \equiv 3\), \(\frac{1}{6} \equiv 6\) (mod 7).
Ahora, dado que \(\frac{1}{5}\) es \(4\), \(\frac{3}{5}\) debería ser \(3 \times 4\), lo que es \(5\), y puedes verificar que
\(\frac{3}{5} \equiv 5\) (mod 7).
\(\frac{2}{3} \equiv 3\), \(\frac{3}{4} \equiv 6\), \(\frac{2}{5} \equiv 6\), \(\frac{3}{5} \equiv 2\), \(\frac{4}{5} \equiv 5\), \(\frac{5}{6} \equiv 2\) (mod 7).
¿Y qué pasa con \(\frac{1}{7}\)? Dado que 7 es lo mismo que 0 módulo 7, esto sería dividir por cero, ¡lo cual es ilegal!
Si estás trabajando módulo un número que no es primo, hay más cosas por las que no puedes dividir. Por ejemplo, módulo 15, cada múltiplo de 3 es uno de 0, 3, 6, 9 o 12, y dado que 1 no aparece, no hay un número \(\frac{1}{3}\) módulo 15, aunque 3 no sea 0 módulo 15.
Aquí hay una manera bastante fácil de encontrar los números \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\), ..., \(\frac{1}{p}\), módulo \(p\). ¿Existe un número \(\frac{1}{8}\) módulo 101? El primer múltiplo de 8 que excede 101 es \(8 \times 13 = 104 \equiv 3 \mod 101\), y así podemos reducir el tamaño del problema:
\(8 \times 13 \equiv 3\).
Ahora el primer múltiplo de 3 después de 101 es \(3 \times 34 = 102 \equiv 1 \mod 101\), lo que implica que
\(3 \times 34 \equiv 1\),
y por lo tanto,
\(8 \times 13 \times 34 \equiv 1\).
Esto nos dice que la respuesta es:
\(\frac{1}{8} \equiv 13 \times 34 \mod 101\).
Esto es sorprendentemente fácil de resolver: sabemos que tres \(34\) son 1, así que doce \(34\) son 4 y trece \(34\) deben ser 38:
\(\frac{1}{8} \equiv 38 \mod 101\).
De la misma manera, podemos encontrar todos los números \(\frac{1}{2}\), \(\frac{1}{3}\), ..., \(\frac{1}{100}\) módulo 101. Si quieres \(\frac{1}{68}\) módulo 101, comienzas con 68 y luego multiplicas repetidamente por el primer número que te permite restar 101 (y así obtener una respuesta más pequeña):
\(68 \to 136 \to 35 \to 105 \equiv 4 \to 104 \equiv 3 \to 102 \equiv 1\).
Por lo tanto, \(\frac{1}{68}\) es \(2 \times 3 \times 26 \times 34\), que es simplemente \(2 \times 26 = 52\), dado que ya sabemos que \(3 \times 34 \equiv 1\).
\(\frac{1}{68} \equiv 52 \mod 101\).
1Módulo un número no primo, este método a veces funciona, pero también puede fallar al llegar a cero. Por ejemplo, módulo 102,
\(68 \to 136 \equiv 34 \to 102 \equiv 0,\) \(5 \to 105 \equiv 3 \to 102 \equiv 0.\)
De hecho, no existe un número \(\frac{1}{68}\) módulo 102, pero sí existe un número \(\frac{1}{5}\), a saber, 41.
¿Se Puede Descomponer un Número en Factores Primos de Más de una Manera?
El famoso libro de Euclides, Los Elementos de Geometría (ca. 300 a.C.), no solo trata de geometría, sino que también proporciona (en el Libro IX) una base teórica para la teoría de números. Su descubrimiento más fundamental sobre los números primos equivale a la afirmación de que cada número se factoriza de una manera única en un producto de primos.
Los factores se dividen de manera única en números primos. Esto no es del todo obvio, y podrías pensar que no es cierto para 1001, ya que:
\(1001 = 7 \times 143 = 11 \times 91.\)
La explicación es sencilla. Aunque 7 y 11 son primos, 143 \(= 11 \times 13\) y 91 \(= 7 \times 13\) no lo son, y la única factorización de 1001 en números que son todos primos es:
\(1001 = 7 \times 11 \times 13 = 11 \times 7 \times 13 = \ldots\)
(el orden no importa). Es fácil demostrar que esto siempre ocurre si conoces el:
Un número primo no puede dividir un producto, a menos que divida uno de los factores.
Porque si \(n = a \times b \times c \times \ldots\) y \(p\) no divide ninguno de \(a, b, c, \ldots,\) entonces, módulo \(p,\) hay números \(1/a, 1/b, 1/c, \ldots,\) y por lo tanto, hay un número \(1/n = 1/a \times 1/b \times 1/c \times \ldots,\) lo que demuestra que \(n\) no puede ser divisible por \(p.\)
El principio de Euclides es lo que impide que un número tenga dos factorizaciones realmente diferentes. Esto se debe a que cualquier primo en una factorización debe dividir algún primo en la otra, por lo que debe ser ese mismo primo. Podemos cancelar este primo y repetir el argumento. Las dos factorizaciones solo pueden diferir en el orden en que están dispuestos los primos.
SIEMPRE HAY NUEVOS PRIMOS
No es obvio que la secuencia de números primos continúe indefinidamente. Allí puede llegar una etapa, tal vez, en la que el proceso de cribado se detiene porque todos los números restantes han sido tachados. Sin embargo, Euclides también demostró que los primos no tienen fin.
Imagina que todos los primos que conoces son:
\(2, 3, 5, 7, 11, 13.\)
Entonces, demostraremos que debe haber otro primo. Multiplica tus primos y añade 1 para obtener un número mayor:
\(2 \times 3 \times 5 \times 7 \times 11 \times 13 + 1 = 30031.\)
Este número ciertamente es mayor que 1. ¿Cuál es el número más pequeño, mayor que 1, que lo divide exactamente? Este debe ser un primo; de lo contrario, uno de sus factores sería un candidato más pequeño. Pero no puede ser uno de los primos anteriores, \(2, 3, 5, 7, 11\) o \(13,\) ya que cada uno de estos deja un residuo 1 cuando se divide entre 30031. Así que hemos encontrado un nuevo primo.
A veces, el número grande aquí ya es primo, pero a veces, como en el ejemplo anterior, no lo es:
\(1 + 1 = 2\) es primo
\(2 + 1 = 3\) es primo
\(2 \times 3 + 1 = 7\) es primo
\(2 \times 3 \times 5 + 1 = 31\) es primo
\(2 \times 3 \times 5 \times 7 + 1 = 211\) es primo
\(2 \times 3 \times 5 \times 7 \times 11 + 1 = 2311\) es primo
pero
\(2 \times 3 \times 5 \times 7 \times 11 \times 13 + 1 = 30031 = 59 \times 509\)
y
\(2 \times 3 \times 5 \times 7 \times 11 \times 13 \times 17 + 1 = 510511 = 19 \times 97 \times 277,\)
mientras que
\(2 \times 3 \times 5 \times 7 \times 11 \times 13 \times 17 \times 19 + 1 = 9699691 = 347 \times 27953.\)
Los próximos números primos de la forma \(2 \times 3 \times 5 \cdots \times p + 1\) son para \(p = 31, 59, 79, 101, 263, 257.\)
Aunque sabemos desde Euclides que los números primos pueden ser tan grandes como se desee, pasó bastante tiempo antes de que los matemáticos pudieran señalar explícitamente algunos números muy grandes.
Números de Mersenne
Antes del auge de las revistas científicas, había varias personas interesadas en comunicar cualquier descubrimiento científico del que se enteraran a una gran cantidad de corresponsales. Marin Mersenne (1588–1648) prestó este servicio a los matemáticos de su época. De hecho, gran parte del trabajo de Fermat fue "publicado" por primera vez a través de las cartas de Mersenne.
En una carta a Frenicle de Bessy, Mersenne discutió las posibilidades de números primos de la forma \(2^n - 1\) y realizó la sorprendente afirmación de que \(2^n - 1\) es primo para \(n = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257\) y para ningún otro \(n\) menor que 257. La afirmación de Mersenne despertó un gran interés porque los números son tan grandes que durante los siguientes 200 años nadie pudo confirmarla ni negarla. Este interés continúa hoy, y los números de la forma \(2^n - 1\) han sido nombrados en honor a Mersenne. ¿Tenían Mersenne o Fermat técnicas desconocidas para alguien más?
En 1876, Édouard Lucas logró probar que \(2^{127} - 1\) era un número nnimo, y este permaneció como el mayor número primo conocido durante más de 70 años. Sin embargo, durante este período se encontraron varios errores en la afirmación de Mersenne, y finalmente quedó claro que no había sido más que una conjetura educada.
Es fácil ver que \(2^n - 1\) definitivamente no es primo si \(n\) en sí mismo no es primo. La expansión binaria de \(2^{15} - 1,\) por ejemplo, es:
\(111 \, 111 \, 111 \, 111 \, 111,\)
lo que obviamente es divisible por los números binarios \(111 = 2^3 - 1\) y \(11111 = 2^5 - 1,\) y por lo tanto no puede ser primo.
Sin embargo, hay números primos \(p\) para los cuales \(2^p - 1\) no es primo. Por ejemplo:
\(2^{11} - 1 = 2047 = 23 \times 89.\)
En decimal, o
\(11111111111 = 10111 \times 1011001\) en binario. Existen técnicas especiales que hacen relativamente fácil probar si un número \(2^p - 1\) es primo y hay una buena posibilidad de que, al leer esto, el mayor primo conocido sea un número de Mersenne. Por ejemplo, en 1951, Miller y Wheeler tuvieron el récord con \(180(2^{127} - 1)^2 + 1,\) y alrededor de 1989–1992, J. Brown et al. lo mantuvieron con:
\(391581 \times 2^{216193} - 1.\)

NÚMEROS PERFECTOS
Los antiguos estaban particularmente intrigados por las ecuaciones:
\(6 = 1 + 2 + 3\)
\(28 = 1 + 2 + 4 + 7 + 14\)
que muestran que tanto 6 como 28 son la suma de todos los números más pequeños que los dividen exactamente. Los llamaron perfectos. Fue sugerido...
Se sugirió que Dios creó el mundo en 6 días porque el número 6 era un número perfecto.
Dos mil años antes de Mersenne, Euclides (Libro IX, Prop. 36) descubrió una interesante conexión entre los números perfectos y lo que ahora llamamos números primos de Mersenne.
Si \( M = 2^p - 1 \) es un primo de Mersenne, entonces el \( M \)-ésimo número triangular,
\[ \Delta_M = \frac{1}{2} M (M + 1) \]es un número perfecto.
Por ejemplo, 31 es un primo de Mersenne, y el número triangular 31 es \( 16 \times 31 = 496 \), cuyos divisores más pequeños son:
1, 2, 4, 8, 16, con suma 31
31, \( 2 \times 31, 4 \times 31, 8 \times 31 \), con suma \( 15 \times 31 \)
Total \( 16 \times 31 \).
Lo mismo ocurre con todos los primos de Mersenne.
¿Hay otros números perfectos? El gran matemático suizo Leonhard Euler (1707–1783) demostró que todos los números perfectos pares son de la forma de Euclides. Todo lo que sabemos de los impares es que deben tener al menos 300 dígitos decimales y muchos factores. ¡Probablemente no hay ninguno!
Números de Fermat
¿Cuáles de los números
11, 101, 1001, 100001, 1000001...
son primos? Bueno, 11 divide los números que son 1 más que las potencias impares de 10:
1001 = \( 11 \times 91; \, 100001 = 11 \times 9091; \, 10000001 = 11 \times 9090901 \); ...
y 1001 divide los que son 1 más que las potencias impares de 100:
1000001 = \( 101 \times 9901; \, 100000000001 = 101 \times 99009901; \)...
y así sucesivamente. Por lo tanto, los únicos que tienen alguna posibilidad de ser primos son aquellos sin factores impares en el exponente. De hecho,
\( 10^1 + 1 = 11 \) es primo, y
\( 10^2 + 1 = 101 \) es primo, pero
\( 10^4 + 1 = 73 \times 137 \) es compuesto, como lo son
\( 10^8 + 1 = 17 \times 5882353, \)
\( 10^{16} + 1 = 353 \times 449 \times 641 \times 1409 \times 69857, \)
\( 10^{32} + 1 = 19841 \times 976193 \times 6187457 \times 834427406578561, \)
\( 10^{64} + 1 = 1265011073 \times 15343168188881937818369 \)
\( \times 5152175252651232674478699068185873, \)
y \( 10^{128} + 1 = 257 \times 15361 \times 453377 \times \) un primo de 116 dígitos.
De hecho, no sabemos si esta secuencia contiene algún primo que no sea 11 y 101.
Podemos realizar tales cálculos en cualquier base. Sigue siendo cierto que:
solo puede ser primo si \( n \) es una potencia de 2.
En 1640, Pierre de Fermat conjeturó que los 2 ejemplos de base 2 eran todos primos. Hoy los números \( 2^{2^n} + 1 \) se llaman números de Fermat. De hecho, como Fermat sabía,
\[ 2^{1} + 1 = 3,\quad 2^{2} + 1 = 5,\quad 2^{4} + 1 = 17,\quad 2^{8} + 1 = 257,\quad \text{y}\quad 2^{16} + 1 = 65537 \]
son todos primos, pero en 1732, Euler descubrió que el siguiente número de Fermat es compuesto:
\[ 2^{32} + 1 = 4294967297 = 641 \times 6700417. \]
En 1880, F. Landry, a la edad de 82 años, mostró que
\[ 2^{64} + 1 = 274177 \times 67280421310721, \]
y en 1975 Brillhart y Morrison encontraron que
\[ 2^{128} + 1 = 59649589127497217 \times 5704689200685129054721. \]
En 1981, Richard Brent y John Pollard factorearon
\[ 2^{256} + 1 = 1238926361552897 \times 93461639715357977769163558199606896584051237541638188580280321. \]
Incluso antes de que se realizaran estas factorizaciones, se sabía que estos números eran compuestos, como se menciona (ver la página 148).
Actualmente, \(2^{224} + 1\), con 5050446 dígitos, es el primero en duda.
Sabemos que Euclides estaba interesado en los números perfectos, cuya teoría involucra los primos de Mersenne, pero no sabemos si alguna vez pensó en los números de Fermat. ¡Debería haberlo hecho!
El gran matemático alemán Carl Friedrich Gauss (1777–1855) demostró como joven que si \(p\) es un número primo de Fermat, entonces un polígono regular con \(p\) lados puede construirse con regla y compás, siguiendo las reglas de Euclides. Gauss dio construcciones para el triángulo y el pentágono, pero antes de Gauss nadie había construido polígonos más grandes. Se dice que Gauss solicitó que un polígono regular de 17 lados fuera inscrito en su lápida. Esto no se hizo, pero hay un polígono regular de 17 lados en un monumento a Gauss en Braunschweig.
Es fácil construir un polígono regular de 85 lados usando construcciones para el pentágono y el polígono de 17 lados, y ya que cualquier ángulo puede ser bisecado, puedes construir polígonos regulares de 170, 340 lados, y, más generalmente,
\[ 2^k p q r \cdots \text{-gons}, \]
donde \(p\), \(q\), \(r\),... son primos de Fermat distintos. Gauss afirmó que estos eran los únicos polígonos regulares construibles con regla y compás.
Los únicos polígonos regulares conocidos con un número impar de lados son aquellos para los cuales el número divide
\[ 2^{32} - 1 = 3 \times 5 \times 17 \times 257 \times 65537 = 4294967295. \]
Los divisores son
1, 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, 196611, 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529207, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295.
William Watkins notó que puedes obtener sus expansiones binarias leyendo las primeras 32 filas del triángulo de Pascal módulo 2:
Así, el número binario
1 es 1
11 es 3
101 es 5
1111 es 15
10001 es 17
...
Es bastante probable que no existan más polígonos impares de este tipo, porque parece probable que
\[ 3, \, 5, \, 17, \, 257 \, \text{y} \, 65537 \]
son los únicos números de Fermat primos.
Podemos demostrar que \(2^{32} + 1\) es compuesto, utilizando congruencias módulo \(p = 641\). Dado que
\[ p = 625 + 16 = 5^4 + 2^4 \, \text{y} \, 2^4 = -5^4, \, \text{módulo} \, p \]
\[ 5 \times 128 = 1 \, \text{y} \, 2^4 = -5^4, \, \text{módulo} \, p \]
Entonces,
\[ 2^{32} = 2^4 \times 2^{28} = -5^4 \times 128^4 = -(-1)^4 = -1. \]
¿Cómo puede alguien demostrar que los números no son primos sin ser capaz de encontrar ningún factor? Otro de los descubrimientos de Fermat proporciona la respuesta.
Prueba de Fermat para primos
Fermat demostró que cualquier número primo impar \(p\) debe satisfacer:
Prueba de Fermat:
\[ b^{p-1} \equiv 1 \, \text{(mod} \, p), \, \text{para cualquier} \, b \, \text{no divisible por} \, p. \]
Entonces, si un número no satisface esta condición, no puede ser primo. Explicaremos por qué la prueba funciona en el Capítulo 6, pero aquí la usaremos para decir que 91 no es primo. Si lo fuera, entonces, según la prueba, \(2^{90}\) sería congruente a 1, módulo 91. Pero, trabajando con módulo 91,
\[ 2^6 = 64 \equiv -27, \]
entonces
\[ 2^{12} = (-27)^2 = 729 \equiv 1 \]
ya que \(8 \times 91 = 728\).
\[ 2^{84} = (2^{12})^7 = 1^7 = 1 \quad \text{y} \quad 2^{90} = 2^84 \times 2^6 = 1 \times (-27), \]
lo cual no es congruente a 1.
La prueba de Fermat parece más difícil que los cálculos necesarios para encontrar la factorización \(91 = 7 \times 13\), pero para números grandes la situación se invierte. Para encontrar los factores de un número de 50 dígitos, el método ingenuo podría necesitar más de \(10^{23}\) divisiones de prueba, lo que tomaría miles de años, incluso en una supercomputadora. Pero la prueba de Fermat puede demostrar que un número es compuesto utilizando solo unos pocos cientos de multiplicaciones de números de 50 dígitos, lo que se puede hacer hoy en una fracción de segundo.
Con una computadora, ahora es bastante fácil probar la primalidad de números, pero factorizar sigue siendo difícil (aunque hay métodos mucho más rápidos que la división de prueba).
El número 341 \(= 11 \times 31\) pasa la prueba de Fermat para la base 2, ¡aunque no es primo! Usando congruencias, esto es fácil. Dado que
\[ 2^5 = +1 \, (\text{mod} \, 31), \]
\[ 2^5 = -1 \, (\text{mod} \, 11), \]
entonces
\[ 2^{10} = +1 \, (\text{mod} \, 11 \, \text{y} \, 31). \]
Podemos deducir de esto que \(2^{10}\) es congruente a 1 (módulo 341) y, por lo tanto, también \(2^{340}\).
Entonces, la prueba de Fermat es necesaria para la primalidad, pero no es suficiente. Dado que \(2^{340} = 56\) (mod 341), la base 3 muestra que 341 es compuesto, pero hay algunos números especiales, los números de Carmichael, que son compuestos, aunque satisfacen la prueba de Fermat para muchas bases.
El número de Carmichael más pequeño es 561, que satisface la prueba de Fermat para todas las bases \(b\) no divisibles por 3, 11 o 17. Esto se debe a que \(b^{560}\) es una potencia de cada uno de \(b^2, b^{10}\) y \(b^{16}\), que, según la prueba de Fermat, son congruentes a 1 módulo 3, 11 y 17, respectivamente.
Sir John Wilson (1741–1793) dio otra prueba para primos:
\[ p \, \text{es primo precisamente cuando} \, (p-1)! \equiv -1 \, (\text{mod} \, p). \]
A diferencia de la prueba de Fermat, la de Wilson es tanto necesaria como suficiente para primos.
¿Qué tan frecuentes son los números primos?
Hasta \(10\), hay 4 primos, por lo que 1 de cada 2.5 números es primo:
| Hasta | Primos | 1 de cada |
|---|---|---|
| \(10^2\) | 25 | 4 |
| \(10^3\) | 168 | 6 |
| \(10^4\) | 1229 | 8.1 |
| \(10^5\) | 9592 | 10.4 |
| \(10^6\) | 78498 | 12.7 |
| \(10^7\) | 664579 | 15 |
| \(10^8\) | 5761455 | 17.3 |
| \(10^9\) | 50847534 | 19.8 |
Parece que, hasta \(10^7\), aproximadamente 1 de cada \(2.3 \ln n\) números es primo. ¿Qué sucede en general?
La ley logarítmica de Legendre
De los números hasta \(N\),
aproximadamente \(1 / \ln N\) es primo,
donde \(l\) es el logaritmo natural de \(N\).
El logaritmo natural de \(N\) es \(2.30258509 \ldots\) veces el logaritmo en base 10 de \(N\) y es aproximadamente igual al número armónico \(N\)-ésimo (ver el Capítulo 9):
\[ H_N = 1 + \frac{1}{2} + \frac{1}{3} + \ldots + \frac{1}{N}. \]
En 1896, casi un siglo después de Adrienne Marie Legendre (1752–1833), Jacques Hadamard y Charles-Jacques de la Vallée-Poussin adivinaron la fórmula aproximada \(N/\ln N\) para el número de primos hasta \(N\).
Una pequeña mejora
Gauss adivinó que la idea de Legendre debería modificarse ligeramente:
De los números cerca de \(N\),
aproximadamente \(1 / \ln N\) son primos.
Esto lleva a una pequeña mejora, \(Li(N)\), en la fórmula de Legendre. La conjetura de Gauss, \(Li(N)\), es el área sombreada bajo la gráfica de \(1/\ln N\) en la Figura 5.2.
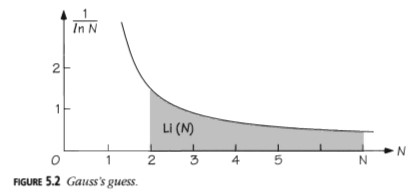
El refinamiento notable de Riemann
En 1859, el gran matemático alemán Georg Friedrich Bernhard Riemann (1826–1866) dio una estimación mucho mejor.
El número de primos hasta \(N\) es aproximadamente:
\[ R(N) = Li(N) - \frac{1}{2}Li(N^{1/2}) - \frac{1}{3}Li(N^{1/3}) - \frac{1}{5}Li(N^{1/5}) + \frac{1}{6}Li(N^{1/6}) - \ldots \]
El coeficiente de \( \frac{1}{n}Li(N^{1/n}) \) es el \(n\)-ésimo número de Möbius, \( \mu(n) \), que es 0 si \(n\) tiene un factor repetido, y \(1\) o \(-1\) si tiene un número par o impar de factores primos.
Ahora se sabe que la conjetura de Gauss, \(Li(N)\), es una mejor estimación que la de Legendre, \(N/\ln N\), y parece que el refinamiento de Riemann es aún mejor. De hecho, bajo algunas suposiciones plausibles, Rubinstein y Sarnak han demostrado que es mejor en aproximadamente el 99.07% de los casos.
Sin embargo, en 1914, John Edensor Littlewood ya había demostrado que ocasionalmente el refinamiento de Riemann es peor que la conjetura de Gauss, y su estudiante, Skewes, mostró que esto tenía que suceder antes de:
\[ 10^{10^{10^{34}}} \quad \text{(el número de Skewes).} \]
No conocemos ningún valor particular de \(N\) para el cual esto suceda, pero Sherman Lehman ha probado que ocurre al menos para \(10^{500}\) números con 1166 o 1167 dígitos decimales.
¿Qué tan buenas son las conjeturas?
La Tabla 5.2 compara las conjeturas de Legendre, Gauss y Riemann:

¿Qué números son suma de dos cuadrados?
Fermat descubrió el fascinante hecho de que un número primo \(p\) puede escribirse como suma de dos cuadrados si \(p+1\) no es divisible por 4. La expresión es entonces única; por ejemplo:
\[ 2 = 1^2 + 1^2, \quad 5 = 2^2 + 1^2, \quad 13 = 3^2 + 2^2, \quad 17 = 4^2 + 1^2, \] \[ 29 = 5^2 + 2^2, \quad 37 = 6^2 + 1^2, \quad 41 = 5^2 + 4^2, \ldots \]
Pero 3, 7, 11, 19, 23, 31, 43, ... no son suma de dos cuadrados. Esto último es fácil de ver: los cuadrados dejan un residuo de 0 o 1 en división por 4.
Por lo tanto, la suma de dos de ellos solo puede dejar un residuo de 0, 1 o 2 al dividir por 4 (Capítulo 2). La mayor parte de la prueba del hecho de Fermat se basa en una propiedad de los números primos complejos de Gauss, y la explicaremos en el Capítulo 8.
Para ver si un número positivo arbitrario es la suma de dos cuadrados, descomponlo en factores primos de la forma:
\[ p^a q^b r^c \ldots \]
Entonces es la suma de dos cuadrados solo si \(p^a + 1\), \(q^b + 1\), \(r^c + 1\), ... no son divisibles por 4.
Por ejemplo, para 1000 \(= 2^3 \cdot 5^3\), miramos \(2^1 + 1 = 1 + 1 = 9\) y \(5^3 + 1 = 126\). Ninguno de estos es divisible por 4, por lo que 1000 no es la suma de dos cuadrados. ¿Puedes encontrarlos? Observa que la representación ya no es necesariamente única: \(1000 = 900 + 100 = 676 + 324\).
Por otro lado, \(999 = 3^3 \cdot 37\) y \(3^3 + 1 = 28\) es divisible por 4, por lo que \(999\) no es la suma de dos cuadrados. Tampoco lo es \(1001 = 7 \times 11 \times 13\), ya que \(7 + 1\) ni \(11 + 1\) ni \(13 + 1\) son divisibles por 4.
Catorce fracciones fructíferas
¿Existe una fórmula simple que dé todos los primos? La mayoría de los matemáticos dirían que no, aunque algunos de ellos han ideado fórmulas artificiales que hacen el trabajo (generalmente basadas en el test de Wilson).
Aquí está nuestro mejor esfuerzo en esta línea, aunque no es exactamente una fórmula:
Comienza con el número 2 y luego multiplícalo repetidamente por las fracciones de la Figura 5.3, lo que dará lugar a una respuesta mucho más amplia. Las letras sobre las flechas de la Figura 5.4 indican qué fracción de estas se está utilizando:
Nota
Ahora se conoce lo siguiente acerca de las factorizaciones de los números de Fermat del noveno al decimotercer términos:
- \(F_9 = 2424833 \times 7455602825647884208337395736200454918783366342657_{p_{99}}\)
- \(F_{10} = 45592577 \times 6487031809 \times 4659775785220018543265460743067778192897_{p_{252}}\)
- \(F_{11} = 319489 \times 974849 \times 167988556341764073517 \times 305688190045843893205135_{p_{564}}\)
- \(F_{12} = 114689 \times 26017793 \times 63766529 \times 190274191361 \times 1256132134125569_{p_{1187}}\)
- \(F_{13} = 2710954639361 \times 263648887757151241313 \times 3603109844542291969 \times 31915460202805516432207627513_{p_{2931}}\)
Referencias
C.L. Baker and F.J. Gruenberger. The First Six Million Prime Numbers. MIC, Madison, WI, 1953.
Fermat's work appears in Book IX of Euclid.
Referencias
Richard P. Brent and John M. Pollard. Factorization of the eighth Fermat number. Math. Comput. 36 (1981): 627–630; MR 83h: 10014.
Richard P. Brent, G.L. Cohen & H.J.J. te Riele. Improved techniques for lower bounds for odd perfect numbers. Math. Comput. 57 (1991): 857–868; MR 92c: 11004.
John Brillhart, D.H. Lehmer, J.L. Selfridge, Bryant Tuckerman, and S.S. Wagstaff. Factorizations of \(b^n \pm 1, b = 2, 3, 5, 6, 7, 10, 11, 12\) up to high powers. Contemp. Math., 22, Amer. Math. Soc., Providence, RI, 1983, 1988; MR 84k: 10005, 90d: 11009.
John Brillhart, Peter L. Montgomery, and Robert D. Silverman. Tables of Fibonacci and Lucas factorizations. Math. Comput. 50 (1988): S1–260 and S1–S15.
Richard E. Crandall, J. Doenias, C. Norrie, and Jeff Young. The twenty-second Fermat number is composite. Math. Comput., 64 (1995): 863–868.
William John Ellison, and M. Mendes-France. Les Nombres Premiers. Hermann, Paris, 1975; translated William and Fern Ellison, Prime Numbers, Wiley, New York, 1985.
Martin Gardner. The Sixth Book of Mathematical Games. W.H. Freeman, San Francisco, 1963; Chapter 9, Patterns and Primes.
Martin Gardner. The remarkable lore of prime numbers. Scientific Amer., 210 no. 3 (Mar. 1964): 120–128.
Richard K. Guy. Conway’s prime producing machine. Math. Mag. 56 (1983): 26–33.
Richard K. Guy. Unsolved Problems in Number Theory, 2nd ed. Springer-Verlag, New York, 1994; Chapter A, Prime Numbers.
A.M. Legendre. Essai sur la Théorie des Nombres. Duprat, Paris, 1808.
R. Sherman Lehman. On the difference \(\pi(x) - \text{li}(x)\). Acta Arith. 11 (1966): 397–410; MR 34: #2546.
J.E. Littlewood. Sur la distribution des nombres premiers. C. R. Acad. Sci. Paris, 158 (1914): 1869–1872.
Paulo Ribenboim. The Book of Prime Number Records. Springer-Verlag, New York, 1988.
Paulo Ribenboim. The Little Book of Big Primes. Springer-Verlag, New York, 1991.
G.F.B. Riemann. Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse, Monatsber. Königl. Preuss. Akad. Wiss. Berlin, 1859, 671.
Hans Riesel. Prime Numbers and Computer Methods for Factorization. Birkhäuser, Boston, 1985.
Michael Rubinstein and Peter Sarnak. Chebyshev’s bias. Experimental Math., 3 (1994): 173–197.
Jeff Young and Duncan Buell. The twentieth Fermat number is composite. Math. Comput., 50 (1988): 261–263.
Más Fructíferos Frutos de las Fracciones
Hasta ahora, nos hemos concentrado en los números enteros. Pero hay muchos otros números, como 2/3, 4/7, ..., que también se comportan de maneras muy interesantes. Los llamaremos simplemente fracciones, aunque los matemáticos suelen referirse a ellas como números racionales. Este curioso nombre proviene del hecho de que un número racional se define como la razón entre dos números enteros.
Esperamos que ya estén familiarizados con los usos más mundanos de las fracciones, por lo que el verdadero tema de este capítulo es cómo las fracciones pueden usarse para arrojar luz sobre algunas propiedades sutiles de los números enteros.
Cada fracción tiene muchas formas: \[ \frac{4}{6} = \frac{2}{3} = \frac{6}{9} = \frac{202}{303} = \ldots \]
La regla de oro para las fracciones es que puedes multiplicar el numerador y el denominador por el mismo número sin afectar el valor de la fracción. Una fracción sin tal factor común está en su forma más simple. La regla de oro también permite sumar, restar, multiplicar y dividir fracciones:
\[ \frac{2}{3} + \frac{1}{4} = \frac{8}{12} + \frac{3}{12} = \frac{11}{12}, \quad \frac{2}{3} \times \frac{1}{4} = \frac{2}{12} = \frac{1}{6}, \quad \frac{\frac{2}{3}}{\frac{1}{4}} = \frac{\frac{8}{3}}{1} = \frac{8}{3}. \]
Fracciones de Farey y Círculos de Ford
El geólogo británico Farey1 sugirió ordenar todas las fracciones propias con denominador (más bajo) hasta cierto punto, en orden de magnitud. Por ejemplo, la sexta serie de Farey es:
\[ 0, \frac{1}{6}, \frac{1}{5}, \frac{1}{4}, \frac{1}{3}, \frac{2}{5}, \frac{1}{2}, \frac{3}{5}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, 1. \]
Estas series tienen muchas propiedades aritméticas interesantes. Por ejemplo, si \(\frac{2}{3}\) y \(\frac{3}{4}\) son fracciones consecutivas en la serie, entonces los "productos cruzados", \(a \times d\) y \(b \times c\), son números consecutivos.
Así, \(\frac{3}{5}\) y \(\frac{2}{3}\) dan los números consecutivos \(3 \times 3 = 9\) y \(5 \times 2 = 10\). Series de Farey más altas se obtienen insertando fracciones: la primera fracción que se inserta entre \(\frac{a}{c}\) y \(\frac{b}{d}\) es siempre el promedio mediado \(\frac{a+b}{c+d}\). Así, para obtener la séptima serie de Farey desde la sexta, se inserta:
\[ \frac{a+b}{c+d}. \]
G.H. Hardy comentó (Notas al Cap. III de An Introduction to the Theory of Numbers) que Farey no publicó nada sobre el tema hasta 1816, cuando afirmó el teorema de que "si \[ \frac{a}{c}, \frac{e}{f}, \frac{b}{d} \] son tres términos sucesivos de una serie de Farey, entonces \[ \frac{e}{f} = \frac{a+b}{c+d}. \] " en una nota en Philos. Mag.. No dio ninguna prueba, y es poco probable que tuviera una, ya que parece haber sido, en el mejor de los casos, un matemático indiferente. Cauchy, sin embargo, vio la afirmación de Farey y proporcionó la prueba (Exer. Math., i, 114-116). Los matemáticos generalmente han seguido el ejemplo de Cauchy al atribuir los resultados a Farey, y la serie sin duda continuará llevando su nombre. "Farey tiene una biografía de veinte líneas en el Dict. National Biog., donde se le describe como geólogo. Como geólogo, se le ha olvidado, y su biógrafo no menciona lo único de su vida que perdura."Advertencia: formar la mediatriz no es la forma de sumar fracciones, a menos que estés calculando promedios de bateo.
Lester R. Ford encontró una representación interesante para las series de Farey. Sobre cada número racional, \( \frac{p}{q} \), en la línea real, dibujamos un círculo de diámetro \( \frac{1}{q^2} \), como en las figuras 6.1, 6.2 y 6.3. Resulta que estos círculos de Ford nunca se superponen, pero a menudo se tocan. De hecho, los círculos en \( \frac{a}{c} \) y \( \frac{b}{d} \) se tocan exactamente cuando \( ad \) y \( bc \) son números enteros consecutivos, y el círculo más grande entre ellos corresponde a la fracción mediatriz, \( \frac{a+b}{c+d} \).
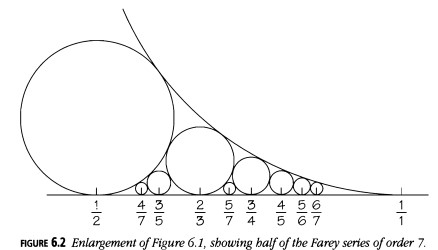
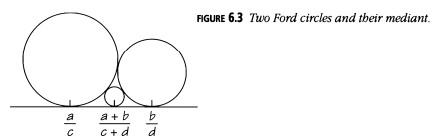
Números Totient de Euler
Mientras estamos en el tema, preguntemos cuántas de las fracciones \( \frac{0}{n}, \frac{1}{n}, \frac{2}{n}, \dots, \frac{n-1}{n} \) tienen como denominador \( n \) el menor posible. Entonces, para \( n = 12 \), estas fracciones se simplifican a
\( \frac{0}{1}, \frac{1}{12}, \frac{1}{6}, \frac{1}{4}, \frac{1}{3}, \frac{5}{12}, \frac{1}{2}, \frac{7}{12}, \frac{2}{3}, \frac{3}{4}, \frac{5}{6}, \frac{11}{12} \),
así que solo las cuatro fracciones \( \frac{1}{12}, \frac{5}{12}, \frac{7}{12} \) y \( \frac{11}{12} \) realmente necesitan ser escritas como doceavos. Aquí hay una pequeña tabla para denominadores pequeños:
| Denominador | Fracciones | Número |
|---|---|---|
| 1 | 0 | 1 |
| 2 | \( \frac{1}{2} \) | 1 |
| 3 | \( \frac{1}{3}, \frac{2}{3} \) | 2 |
| 4 | \( \frac{1}{4}, \frac{3}{4} \) | 2 |
| 5 | \( \frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5} \) | 4 |
| 6 | \( \frac{1}{6}, \frac{5}{6} \) | 2 |
| 7 | \( \frac{1}{7}, \frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7} \) | 6 |
| 8 | \( \frac{1}{8}, \frac{3}{8}, \frac{5}{8}, \frac{7}{8} \) | 4 |
| 9 | \( \frac{1}{9}, \frac{2}{9}, \frac{4}{9}, \frac{5}{9}, \frac{7}{9}, \frac{8}{9} \) | 6 |
| 10 | \( \frac{1}{10}, \frac{3}{10}, \frac{7}{10}, \frac{9}{10} \) | 4 |
El número totiente de Euler
Para un n general, el número de estas fracciones se llama el número totiente de Euler, \(\phi(n)\). Nuestra tabla muestra que:
\[ \phi(1) = 1, \quad \phi(2) = 1, \quad \phi(3) = 2, \quad \phi(4) = 2, \quad \phi(5) = 4, \quad \phi(6) = 2, \quad \phi(7) = 6, \quad \phi(8) = 4, \quad \phi(9) = 6, \quad \phi(10) = 4. \]
Parece que cada número totiente que ocurre, ocurre al menos dos veces, pero nadie ha logrado probar esto aún. Si hay alguno que no ocurre dos veces, debe tener más de 10,000 dígitos.
¿Cuál es el centésimo número totiente, \(\phi(100)\)? Una fracción con denominador 100 se simplificará solo si el numerador no es divisible por 2 o 5. La mitad de los casos son impares, y 4 de cada 5 del resto no se dividen entre 5, por lo que:
\[ \phi(100) = 100 \times \frac{1}{2} \times \frac{4}{5} = 40 \]
es el número de fracciones propias no cancelables con denominador 100.
De manera similar, el número totiente n-ésimo, \(\phi(n)\), es:
\[ n \times \left(1 - \frac{1}{p}\right) \times \left(1 - \frac{1}{q}\right) \times \left(1 - \frac{1}{r}\right) \times \ldots, \]
donde \(p, q, r, \ldots\) son los diferentes divisores primos de \(n\).
Organicemos las 12 fracciones \(0/12, 1/12, \ldots, 11/12\) según su denominador después de simplificarlas:
¿Cuánto mide una serie de Farey?
La respuesta es obviamente que la serie de Farey de orden \(n\) tiene longitud:
\[ 1 + \phi(1) + \phi(2) + \phi(3) + \ldots + \phi(n - 1) + \phi(n) \]
(el 1 inicial proviene del hecho de que contamos \(0/1\) y \(1/1\)).
No hay una fórmula simple para esta suma particular de números totientes, pero se sabe que la respuesta es aproximadamente:
\[ 3 \frac{n^2}{\pi^2} \approx 0.3039635509 \times n^2 \]
y que la aproximación mejora proporcionalmente a medida que \(n\) se hace más grande. Por ejemplo, la décima serie de Farey tiene longitud 33, en comparación con \(3 \times 100/\pi^2 \approx 30.4\), y la centésima tiene longitud 3045, en comparación con \((3 \times 10^4)/\pi^2 \approx 3039.6\).
Las fracciones se transforman en decimales
Todo aquel que haya jugado con números debe haber notado las relaciones entre las fracciones con el mismo denominador:
\[ \frac{1}{7} = 0.1428571428571428 \ldots \]
\[ \frac{2}{7} = 0.2857142857142857 \ldots \]
\[ \frac{3}{7} = 0.4285714285714285 \ldots \]
\[ \frac{4}{7} = 0.5714285714285714 \ldots \]
\[ \frac{5}{7} = 0.7142857142857142 \ldots \]
\[ \frac{6}{7} = 0.8571428571428571 \ldots \]
Un único ciclo de dígitos repetidos funciona para las seis fracciones, como se muestra en la Figura 6.4(a). Sin embargo, cuando llegamos a los treceavos:
\[ \frac{1}{13} = 0.0769230769230769 \ldots \]
\[ \frac{2}{13} = 0.1538461538461538 \ldots \]
\[ \frac{3}{13} = 0.2307692307692307 \ldots \]
... encontramos que hay dos ciclos diferentes (Figuras 6.4(b) y (c)).
Todo el mundo sabe que también hay dos ciclos diferentes para el denominador 3:
\[ \frac{1}{3} = 0.333333 \ldots, \quad \frac{2}{3} = 0.666666 \ldots \]
y posiblemente conoces los cinco ciclos diferentes para 11:
\[ \frac{1}{11} = 0.09090 \ldots, \quad \frac{2}{11} = 0.18181 \ldots, \quad \frac{3}{11} = 0.27272 \ldots, \quad \frac{4}{11} = 0.36363 \ldots, \quad \frac{5}{11} = 0.45454 \ldots \]
y que \(\frac{6}{11}, \frac{7}{11}, \frac{8}{11}, \frac{9}{11}, \frac{10}{11}\) son iguales, cada una comenzando un dígito después. La tabla 6.1 muestra los ciclos para todos los otros primos menores de 100.
¿Por qué las fracciones para un denominador dado se agrupan en ciclos como estos? Algunas respuestas son fáciles, y otras todavía son difíciles de entender.
Es fácil ver cómo ocurren los ciclos: si multiplicamos la expansión de \( \frac{1}{7} \) por 10, obtenemos:
\[ 1.428571428 \ldots = 10 \left( \frac{1}{7} \right) = \frac{10}{7} = 1\frac{3}{7} \]
Y así, de hecho:
\[ 0.428571\ldots = \frac{3}{7}, \]
y:
\[ 14.285714285 \ldots = \frac{100}{7} = 14 \frac{2}{7}. \]
Las fracciones cíclicas en decimales
Se puede observar que esto es así porque:
\[ 10 \equiv 3 \mod 7, \quad 10^2 \equiv 2 \mod 7, \quad 10^3 \equiv 6 \mod 7, \]
\[ 10^4 \equiv 4 \mod 7, \quad 10^5 \equiv 5 \mod 7, \quad 10^6 \equiv 1 \mod 7. \]
Es decir, \(1/7\) tiene la misma parte fraccional que \(3/7\), \(100/7\) tiene la misma parte fraccional que \(4/7\), y así sucesivamente.
En otras palabras, obtienes los numeradores en el orden cíclico:
\[ 1, 3, 2, 6, 4, 5, 1, 3, 2, \ldots, \]
simplemente multiplicando repetidamente por 10 módulo 7.
La razón por la que las fracciones con denominador 13 tienen más de un ciclo es que, módulo 13, las potencias de 10 se repiten con periodo 6:
\[ 10^0 = 1, \quad 10^1 = 10, \quad 10^2 = 9, \quad 10^3 = 12, \quad 10^4 = 3, \quad 10^5 = 4, \quad 10^6 = 1, \]
y por lo tanto, el primer ciclo no contiene todas las fracciones.
Obviamente, para un denominador \(p\),
Los ciclos en la Tabla 6.1, para un denominador dado, tienen todos la misma longitud. Por ejemplo, el denominador 73 da nueve ciclos de 8:
\[ \frac{1}{73} = 0.01369863\ldots, \quad \frac{2}{73} = 0.02739726\ldots, \quad \frac{3}{73} = 0.04109589\ldots, \]
\[ \frac{4}{73} = 0.05479452\ldots, \quad \frac{5}{73} = 0.06849315\ldots, \quad \frac{6}{73} = 0.08219178\ldots, \]
\[ \frac{9}{73} = 0.12328767\ldots, \quad \frac{11}{73} = 0.15068493\ldots, \quad \frac{12}{73} = 0.16438356\ldots. \]

¿Por qué ocurre esto? Bueno, sumar copias de un decimal periódico no puede hacer que la longitud del ciclo sea mayor (aunque podría hacerla más corta), por lo que, por ejemplo, la longitud para \( \frac{20}{73} \) no es mayor que para \( \frac{1}{73} \), ya que:
\[ \frac{1}{73} + \frac{1}{73} + \cdots + \frac{1}{73} = \frac{20}{73}, \]
pero también:
\[ \frac{20}{73} + \frac{20}{73} + \frac{20}{73} + \cdots + \frac{20}{73} = \frac{220}{73} = 3 + \frac{1}{73}, \]
ya que \(11 \times 20 = (3 \times 73) + 1\), y por lo tanto, la longitud del ciclo para \( \frac{1}{73} \) no es mayor que para \( \frac{20}{73} \). Así que deben ser iguales.
¿Cómo encontramos el número 11, que "deshizo" \(20\), módulo 73? En el Capítulo 3 vimos que todos los números \( \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \ldots, \frac{1}{72} \) existen, módulo 73, y explicamos cómo calcularlos. Si haces esto para \( \frac{1}{20} \), módulo 73, encontrarás que es 11. Así que siempre hay un "multiplicador" inverso...
Se puede ver en la Tabla 6.2 que hay bastantes primos para los que el período decimal de \( \frac{1}{p} \) alcanza su longitud completa, \( p-1 \). A estos los llamaremos primos largos (para base 10). Por supuesto, en cada caso en la Tabla 6.2,
\[ \text{número} \times \text{longitud} = p - 1; \]
ya que, en conjunto, los ciclos se encargan de todos los \( p-1 \) numeradores \(1, 2, \ldots, p-1\).

Tanto el número como la longitud de los ciclos deben dividir exactamente \(p - 1\). Pero ya sabemos cuál es la longitud:
y esto divide exactamente a \(p - 1\). Por ejemplo, para \(p = 73\), los ciclos tienen longitud 8, ya que:
\[ 10^8 \equiv 1 \mod 73, \]
y, de hecho, 8 divide a 72. Si tomas la novena potencia de ambos lados de esto, verás que:
\[ 10^{72} \equiv 1 \mod 73. \]
De la misma manera,
\[ 10^{p-1} \equiv 1 \mod p, \]
para cada número primo \(p\) distinto de 2 o 5. Y no hay nada especial sobre la base 10: podemos usar cualquier otra base, \(b\).
Teorema "pequeño" de Fermat
Barajado repetido
Por supuesto, la razón habitual para barajar cartas es mezclarlas, y cuanto más las barajas, más mezcladas esperas que estén. Sin embargo, si repites exactamente el mismo barajado el número correcto de veces, encontrarás que las cartas vuelven a su orden original. Descubriremos este número para tres tipos de barajado: el barajado interno y externo y el barajado de Monge.
Barajados "Riffle"
Estos son frecuentemente utilizados por magos y manipuladores de cartas (Figura 6.5). Divides un mazo de \(2n\) cartas en dos mitades, \(n\) cartas en cada una, y luego las entrelazas de manera alternada para que las cartas en el mazo final provengan alternadamente de tu mano izquierda y derecha (el barajado interno, Figura 6.5(a)), o de tu mano derecha e izquierda (el barajado externo, Figura 6.5(b)). Nota que en el barajado externo, las cartas externas permanecen donde están: solo estás barajando las \(2n-2\) cartas internas.
En el barajado interno verás que las cartas que hemos numerado:
1, 2, 3, 4, 5, 6, 7, 8
terminan en las posiciones originalmente ocupadas por los números:
2, 4, 6, 8, 1, 3, 5, 7.
La regla general es que la carta número \(k\) termina en el lugar que estaba originalmente ocupado por la carta cuyo número era \(2k\), módulo \(2n+1\). Después de \(s\) barajados, la carta número \(k\) estará en el lugar que estaba originalmente ocupado por la carta cuyo número era \(2^s k\), módulo \(2n+1\), por lo que \(s\) barajados restaurarán el orden original solo cuando:
Por el pequeño teorema de Fermat, cuando \(2n+1\) es un número primo, \(p\), el número requerido de barajados siempre divide \(p-1 = 2n\), el número de cartas.
Ocurre que 53 es un primo largo en la base 2, por lo que necesitas exactamente 52 barajados para restaurar el orden original a un mazo de 52 cartas.
Para el barajado externo numeramos las cartas desde 0 como en la Figura 6.5(b) y obtenemos resultados similares: \(s\) barajados restaurarán el orden justo cuando:
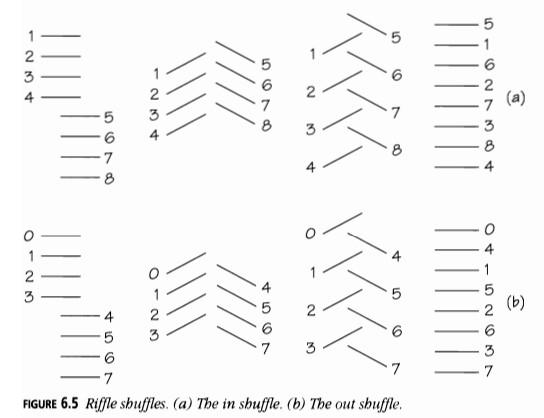
Barajado de Monge
Gaspard Monge investigó el siguiente tipo de barajado. Toma cartas desde la parte superior del mazo en tu mano izquierda alternativamente hacia la parte inferior y superior del mazo en tu mano derecha, como se muestra en la Figura 6.6.
Esta vez, el lugar originalmente ocupado por la carta \(k\) es aquel cuyo número es congruente a \(\pm 2k, \mod 4n+1\). El número de barajados necesarios para restaurar el orden original es el menor \(s\) para el cual:
Si \(4n+1\) es primo, este número divide \(2n\):
Así que verás que los barajados de cartas realmente están investigando el comportamiento cíclico de las fracciones en base 2.
¿Cómo cambia la longitud del ciclo con la base?
La longitud del ciclo de \(1/p\) sí depende de la base de notación, \(b\), (pero porque es el menor \(n\) para el cual \(b^n \equiv 1 \mod p\), realmente depende solo del valor de \(b \mod p\)). Veamos \(1/13\) en diferentes bases (Tabla 6.3).
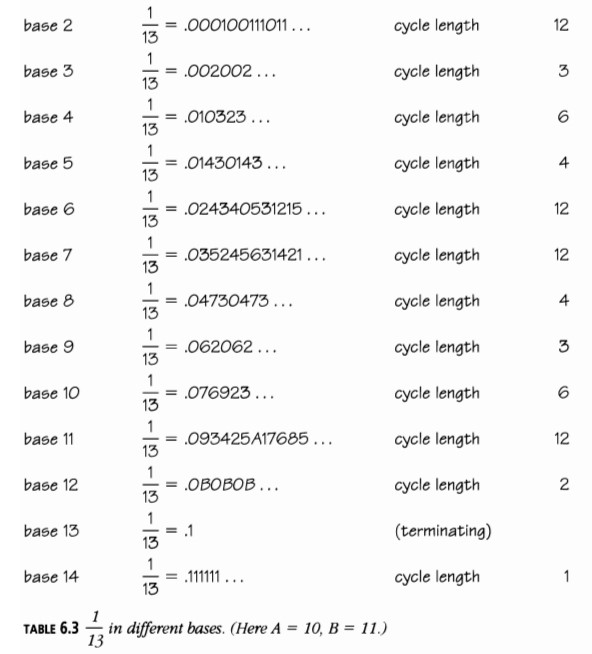
Así que la longitud es:
12 para las 4 clases \( b \equiv 2,6,7,11 \mod 13 \)
6 para las 2 clases \( b \equiv 4,10 \mod 13 \)
4 para las 2 clases \( b \equiv 5,8 \mod 13 \)
3 para las 2 clases \( b \equiv 3,9 \mod 13 \)
2 para la 1 clase \( b \equiv 12 \mod 13 \)
1 para la 1 clase \( b \equiv 1 \mod 13 \)
Compara esto con el comportamiento de las fracciones \( \frac{0}{12}, \frac{1}{12}, \frac{5}{12}, \frac{7}{12}, \frac{11}{12} \). El denominador más bajo es:
12 para las 4 fracciones \( \frac{1}{12}, \frac{5}{12}, \frac{7}{12}, \frac{11}{12} \)
6 para las 2 fracciones \( \frac{1}{6}, \frac{5}{6} \)
4 para las 2 fracciones \( \frac{1}{4}, \frac{3}{4} \)
3 para las 2 fracciones \( \frac{1}{3}, \frac{2}{3} \)
2 para la 1 fracción \( \frac{1}{2} \)
1 para la 1 fracción \( \frac{0}{1} \).
En general, como descubrió Euler:
Regla del Totiente de Euler
El número de bases, módulo \( p \), en las cuales \( \frac{1}{p} \) tiene una longitud de ciclo \( l \), es exactamente igual al número de fracciones:
que tienen el menor denominador \( l \). Para comprender esto, debemos usar un poco de álgebra, específicamente el hecho de que una ecuación no puede tener más raíces (soluciones) que su grado. Esto se prueba utilizando únicamente las cuatro reglas aritméticas, así que:

Aquí vemos que:
\( x^2 - 1 \) tiene exactamente 2 raíces \( \mod \; 13 \)
\( x^3 - 1 \) tiene exactamente 3 raíces \( \mod \; 13 \)
\( x^4 - 1 \) tiene exactamente 4 raíces \( \mod \; 13 \)
\( x^6 - 1 \) tiene exactamente 6 raíces \( \mod \; 13 \)
\( x^{12} - 1 \) tiene exactamente 12 raíces \( \mod \; 13 \).
O, en otras palabras:
\( 2 \) bases, \( \mod \; 13 \), producen longitud dividiendo 2.
\( 3 \) bases, \( \mod \; 13 \), producen longitud dividiendo 3.
\( 4 \) bases, \( \mod \; 13 \), producen longitud dividiendo 4.
\( 6 \) bases, \( \mod \; 13 \), producen longitud dividiendo 6.
\( 12 \) bases, \( \mod \; 13 \), producen longitud dividiendo 12.
Desde estos datos, puedes calcular cuántas bases, módulo 13, producen cada longitud posible: es exactamente lo mismo que las fracciones \( \frac{0}{12}, \frac{1}{12}, \frac{5}{12}, \dots \frac{11}{12} \). Este comportamiento explica la regla del totiente de Euler.
Teorema de Wilson
Sir John Wilson (1741–1793) observó que cuando \( p \) es un número primo, los números factoriales \((p - 1)!\) siempre dejan como residuo \( p - 1 \) al dividirse por \( p \).
Explicamos esto de la siguiente manera:
\[ (x - 1)(x - 2)(x - 3) \cdots (x - (p - 1)) \equiv x^{p-1} - 1 \pmod{p}. \]
Si necesitas más información o tienes dudas sobre algún concepto, no dudes en pedírmelo.
Teorema de Wilson
Para todos los primos p,
\[ (p - 1)! \equiv -1 \pmod{p} \]Primos Largos
Los primos largos son aquellos para los cuales el período de \( \frac{1}{p} \) tiene la longitud completa \( p - 1 \). Para la base 10, estos son:
7, 17, 19, 23, 29, 47, 59, 61, 97, 109, 113, 131, 149, 167, ...
Parece que aproximadamente el 37% de los primos son largos en base 10. El ilustre Emil Artin sugirió que este número es realmente:
donde hay un factor \( \frac{p^2 - p - 1}{p^2 - p} \) para cada número primo p.
Aunque 7 es largo en base 10, no lo es en base 2, ya que las potencias de 2 repiten con período 3, módulo 7:
Por otro lado, 13 es largo en base 2, pero no en base 10. Por la regla del totiente de Euler, siempre hay bases en las que p es largo, ya que ciertamente hay fracciones con menor denominador \( p - 1 \). De hecho:
\( p \) es largo en exactamente \( \phi(p - 1) \) bases, módulo \( p \).
¿Cuántos primos largos pensamos que hay para varias bases?
Parece haber aproximadamente la misma proporción, \( C \), de primos largos en base 2 que en base 10, pero para otras bases, aparentemente obtenemos diferentes múltiplos fraccionales de \( C \), según la conjetura de Artin, modificada por Dick Lehmer (Tabla 6.4).
No se ha probado esto ni siquiera demostrado que exista alguna base en la que haya infinitamente muchos primos largos, pero algún trabajo profundo de Christopher Hooley lo hace parecer muy probable.
No dejes que el hecho de que nos hemos concentrado en fracciones con denominadores primos te haga pensar que esos son los únicos casos interesantes. Hay muchos patrones bonitos con otras denominadores. Por ejemplo:
Si tomas un número de la forma:
entonces el decimal obtenido al invertir los seis dígitos del período, \( fedcbafedcba ... \), es otro número de la forma:
Por ejemplo:
- \( \frac{13}{91} = .142857 \), mientras que \( \frac{75824}{91} = .758241 \).
- \( \frac{7}{91} = .076923 \), mientras que \( \frac{32967}{91} = .329670 \).
- \( \frac{1}{91} = .010989 \), mientras que \( \frac{98900}{91} = .989010 \).
Los ciclos restantes son:
- \( \frac{5}{91} = .054945 \).
- \( \frac{2}{91} = .021978 \), y \( \frac{87}{91} = .879120 \).
- \( \frac{4}{91} = .043956 \), y \( \frac{65}{91} = .659340 \).
- \( \frac{2}{13} = .153846 \), y \( .648351 = \frac{59}{91} \).
- \( \frac{24}{91} = .263736 \), y \( .637362 = \frac{58}{91} \).
Fracciones Pitagóricas
Como veremos en el capítulo 7, los problemas de geometría no siempre conducen a números racionales, pero hay algunos casos interesantes donde sí lo hacen. ¿Qué formas de rectángulos tienen lados y diagonales con números enteros? Llamaremos a las fracciones correspondientes \( b/l \) las fracciones pitagóricas (Figura 6.7). Aquellos lectores que recuerden el triángulo 3, 4, 5 verán que \( 3/4 \) y \( 4/3 \) son fracciones pitagóricas.

El famoso aritmético griego Diofanto de Alejandría demostró que las fracciones pitagóricas son precisamente los números:
con \( p \) y \( q \) como números enteros.
Aquí están todos los triángulos rectángulos con lados enteros y catetos menores de 100 (omitiendo aquellos donde \( b \), \( l \) y \( d \) tienen un factor común):
- 3, 4, 5
- 5, 12, 13
- 7, 24, 25
- 8, 15, 17
- 9, 40, 41
- 11, 60, 61
- 12, 35, 37
- 13, 84, 85
- 16, 63, 65
- 20, 21, 29
- 20, 99, 101
- 28, 45, 53
- 33, 56, 65
- 36, 77, 85
- 39, 80, 89
- 48, 55, 73
- 60, 91, 109
- 65, 72, 97
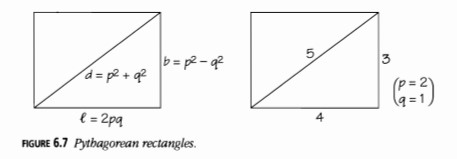

La Figura 6.9 ilustra el método de Vogeler para encontrar fracciones pitagóricas. Este enfoque usa un círculo y un cuadrado para visualizar las fracciones que corresponden a triángulos rectángulos con números enteros.
Una Tabla Babilónica de Fracciones Pitagóricas
Estas "fracciones pitagóricas" eran conocidas mucho antes de Pitágoras. La Figura 6.10(a) muestra una tablilla de arcilla babilónica que se cree registraba algunas transacciones comerciales antes de que Otto Neugebauer señalara su conexión con las ternas pitagóricas.
En el Capítulo 1 aprendimos a leer escritura cuneiforme babilónica, por lo que podrás verificar la traducción dada en la Figura 6.10(b). La tablilla está claramente rota. Hay varias especulaciones sobre el alcance exacto (¡y uso!) de la tabla original, pero nuestra propia reconstrucción se muestra en la Figura 6.11. Según esto, la tabla completa podría haber registrado todas las formas:
longitud : ancho : diagonal
proporcional a
\[ 2pq : p^2 - q^2 : p^2 + q^2 \]con \( p \) y \( q \) como números "regulares" (es decir, que dividen poderes de 60) y \( q \) menor que 60. En el Capítulo 7 veremos cómo encontrar fracciones que sean buenas aproximaciones a otros números.


Fracciones continuas
En nuestro esfuerzo por comprender el mundo, a menudo nos encontramos reemplazando los números desordenados que nos rodean por aproximaciones simples, diciendo que una pulgada es 2½ centímetros, o que un litro es 2½ pintas, o 1⅓ pintas, dependiendo de qué lado del Atlántico nos encontremos.
Los antiguos se enfrentaron a varias de estas preguntas en contextos astronómicos y encontraron, por ejemplo, pero no con tanta precisión, que las estaciones se repiten cada 365.242199 días: lo llamaremos un año, mientras que el periodo de las fases de la luna es 29.530588 días: lo llamaremos un mes. De hecho, los números 365.242199 y 29.530588 decrecen cada siglo en 1 o 2 en el último decimal debido a la fricción de las mareas, que está ralentizando la rotación de la Tierra y haciendo el día más largo. Sin embargo, su relación, que es todo lo que usaremos, es sensiblemente constante.
El astrónomo ateniense Metón (ca. 432 a.C.) descubrió que 235 meses son muy aproximadamente iguales a 19 años. Este es el ciclo Metónico, que todavía se usa para determinar el calendario judío y también la fecha de la Pascua.
La Figura 6.12 ilustra este error al comparar varios números de meses con varios números de años. Las primeras dos líneas indican el número de días en el año y en el mes. Cada línea subsiguiente se encuentra agregando o restando un múltiplo de las fracciones mostradas para reducir el error, el múltiplo que se elige es el que reduce el error a un nuevo mínimo. Por ejemplo, obtenemos la sexta línea agregando dos veces la quinta a la cuarta, ya que esto da un nuevo error mínimo:
(si solo hubiéramos agregado una copia, habríamos tenido 7.78 ... - 3.09 ... = 4.68 ..., no un nuevo récord).
Así que vemos que el error de 0.0864 de un día (2 horas y 4.4 minutos) en la aproximación de Metón no se mejora hasta que comparamos 4131 meses con 334 años. Las fracciones sucesivas:
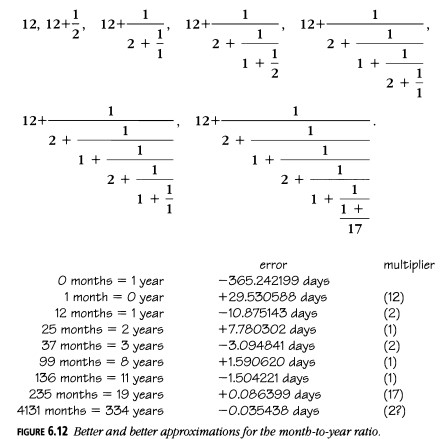
Figura 6.12: Mejores y mejores aproximaciones para la relación mes-año.
Diseño de trenes de engranajes
Los ingenieros usan esto en el diseño de trenes de engranajes. La Figura 6.13 muestra un tren de engranajes simple que podría usarse en un planetario para simular el movimiento relativo del sol y la luna alrededor de la Tierra. Aproxima 12.368267 ... por 235/19.
Nos encontramos con fracciones continuadas nuevamente en nuestro próximo capítulo, que comienza con otra pieza de las matemáticas babilónicas.
Figura 6.13: Tren de engranajes que simula el movimiento relativo del sol y la luna.
Referencias
David Aldous and Persi Diaconis. Shuffling cards and stopping times. Amer. Math. Monthly, 93 (1986) no. 5, 333–348. (Tiene una extensa bibliografía).
Persi Diaconis, R.L. Graham and William M. Kantor. The mathematics of perfect shuffles. Adv. Appl. Math., 4 (1983): 175–196.
C. Hooley. On Artin’s conjecture. J. reine angew. Math., 225 (1967): 209–220; M.R. 34 #7445.
C.G.J. Jacobi. Canon Arithmeticus, Berlin, 1839; Nach Berechnungen von Wilhelm Patz, en verbesserter und erweiterter Form neu herausgegeben von H. Brandt, Akademie-Verlag, Berlin, 1956.
Otto Neugebauer. The Exact Sciences in Antiquity. Princeton Univ. Press, Princeton, NJ, 1952.
A.E. Western and J.C.P. Miller. Indices and primitive roots. Royal Society Math. Table, 9, Cambridge Univ. Press, 1968.
Samuel Yates. Prime Period Lengths (publicado de manera privada).