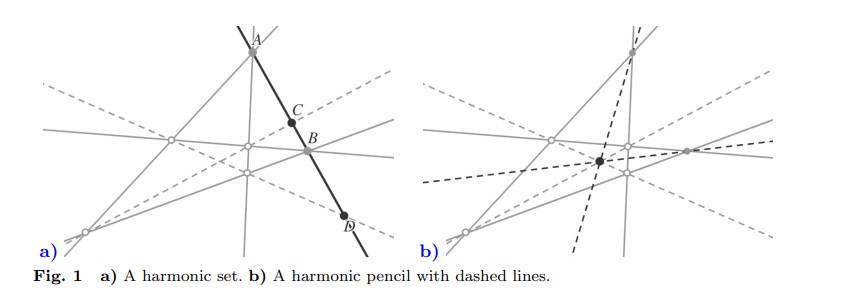
Figura 1: a) Un conjunto armónico. b) Un haz armónico con líneas discontinuas.
El propósito de este artículo es presentar la geometría proyectiva de una manera sintética, visual e intuitiva a través de la noción central de armonicidad, que conduce a las curvas armónicas. Esta presentación incluye nuevos resultados, pruebas inéditas de algunos teoremas clásicos y una ligera reformulación de su axiomatización.
Armonicidad, Curvas Cónicas, Superficies Regladas, Geometría Proyectiva
51A05, 97G10, 97G40, 51A30
Una curva o sección cónica se define como la intersección de un cono circular con un plano. Este concepto es inherentemente métrico. Sin embargo, es bien conocido que las curvas cónicas pertenecen de alguna manera a la geometría proyectiva, aunque no está claro cómo. Por ejemplo, la afirmación de que las elipses son lo que vemos al mirar un círculo, que es cómo deberíamos presentarlas a los niños, resulta incómoda para muchos porque no lo escuchamos en clase y no tenemos una prueba sencilla a mano. Tratando de comprender este estado de cosas incongruente, nos llevó a definir curvas armónicas en un estilo puramente proyectivo (básicamente, son el lugar geométrico de puntos en el plano que ven un cuadrángulo como un conjunto armónico) y estudiar sus propiedades sin ninguna referencia a conceptos métricos. Sí, las curvas armónicas se convierten en secciones cónicas en el plano euclidiano, pero tienen un conjunto rico de propiedades puramente proyectivas, por lo que su estudio constituye un enfoque hermoso hacia la geometría proyectiva. Este enfoque es de lo que trata este artículo.
Motivados por las técnicas de dibujo en perspectiva, descubiertas por los pintores del Renacimiento para representar de manera realista escenas tridimensionales en lienzos planos, Girard Desargues (1591-1661) inició el desarrollo de la Geometría Proyectiva, expandiendo el concepto de espacio para incluir puntos ideales (también conocidos como puntos en el infinito) [6]. Olvidado en gran medida durante los dos siglos siguientes, su trabajo visionario fue revivido y reconocido como fundamental durante la primera mitad del siglo XIX, cuando la Geometría Proyectiva se estableció firmemente como un campo propio. En 1872, Felix Klein abrió su famoso Programa de Erlangen [9] con la declaración "Entre los avances de los últimos cincuenta años en el campo de la geometría, el desarrollo de la Geometría Proyectiva ocupa el primer lugar". Uno de los matemáticos cuyo trabajo mereció tal elogio fue Karl Georg Christian von Staudt (1798-1867). En su tratado sobre el tema [13], demostró que las nociones de armonicidad, es decir, los conceptos de conjuntos armónicos y haces armónicos, son enteramente proyectivos e independientes de conceptos métricos como distancias o ángulos. También muestra que las curvas cónicas pueden definirse mediante el concepto abstracto y puramente proyectivo de polaridad.
Una de las contribuciones fundamentales de Karl von Staudt fue demostrar que la armonicidad (la noción de conjugados armónicos, que se ha usado desde la antigüedad en términos de distancias) depende únicamente de la incidencia, utilizando cuadrángulos.
Un cuadrángulo, \( Q \), se define como cuatro puntos en el plano proyectivo en posición general (es decir, no hay tres de ellos colineales), llamados sus vértices, junto con cuatro líneas, llamadas sus lados, de modo que su relación de incidencia forma un ciclo de cuatro (cada objeto de un tipo es incidente con dos del otro); es decir, \( Q \) se define por sus vértices (4 puntos en posición general) junto con un orden diédrico (es decir, cíclico pero no orientado) sobre ellos que determina los 4 lados.

Figura 1: a) Un conjunto armónico. b) Un haz armónico con líneas discontinuas.
Cuatro puntos colineales \( A, C, B, D \), como en la Figura 1.a, forman un conjunto armónico si existe un cuadrángulo tal que sus puntos diagonales son \( A \) y \( B \) (por lo tanto, el horizonte del cuadrángulo es su línea de soporte) y el otro par, \( C \) y \( D \), son incidentes con las diagonales.
La Figura 1.b muestra un haz armónico con líneas discontinuas.
Cuatro puntos en posición general son los vértices de tres cuadrángulos. Sus correspondientes centros y horizontes forman su triángulo diagonal.
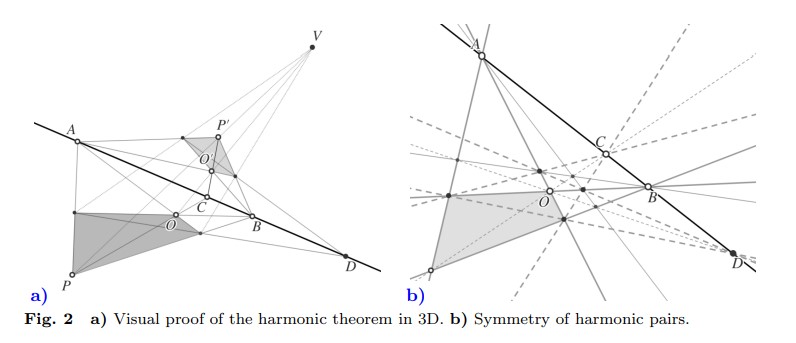
Figura 2: a) Prueba visual del teorema armónico en 3D. b) Simetría de pares armónicos.
Cuatro puntos colineales \( A, C, B, D \), como en la Figura 1.a, forman un conjunto armónico si existe un cuadrángulo tal que sus puntos diagonales son \( A \) y \( B \) (por lo tanto, el horizonte del cuadrángulo es su línea de soporte) y el otro par, \( C \) y \( D \), son incidentes con las diagonales.
La Figura 1.b muestra un haz armónico con líneas discontinuas.
El resultado de la construcción armónica no depende de la elección de los puntos auxiliares.
La prueba es bien conocida y se deriva del Teorema de Desargues. También puede probarse directamente en 3D utilizando solo argumentos de incidencia (ver Figura 2.a), deduciendo inmediatamente el caso plano de ello. Omitimos los detalles por brevedad.
Finalmente, para ver que la definición de conjunto armónico es simétrica respecto al rol de los dos pares de puntos, extendemos el cuadrángulo \( Q \) a un mosaico 2x2 dibujado en perspectiva, como en la Figura 2.b (el saber hacer proviene de los artistas renacentistas y las coincidencias se derivan del Teorema Armónico). Luego, el cuadrilátero de diagonales (discontinuas) que no son incidentes con su centro \( O \) demuestra que \( A \) y \( B \) son conjugados armónicos con respecto a \( C \) y \( D \).
Como el punto \( O \) en la Figura 2.b puede elegirse como cualquier punto fuera de la línea de soporte del conjunto armónico, obtenemos que cualquier punto así los ve como armónicos, es decir, las líneas hacia ellos con su orden diédrico forman un haz armónico. Dualmente, también existe una construcción armónica para líneas, y cualquier línea que no pase por el centro de un haz armónico lo corta en un conjunto armónico. Por lo tanto, los conjuntos y haces armónicos se preservan mediante proyecciones.
Definimos la curva armónica \( C_Q \) de un cuadrángulo \( Q \) como el lugar geométrico de puntos que son centros de haces armónicos transversales a \( Q \). Por transversal, nos referimos a que cada vértice de \( Q \) es incidente con una línea del haz y esta correspondencia conserva los órdenes diédrico. Dualmente, el haz armónico de un cuadrilátero consiste en las líneas que soportan un conjunto armónico transversal a sus lados y con órdenes diédrico correspondientes.
Consideremos un cuadrángulo \( Q \) con vértices \( A, C, B, D \). Primero observamos que los vértices son puntos de su curva armónica \( C_Q \). En efecto, para cada vértice, el conjugado armónico de su diagonal respecto a sus lados completa un haz armónico centrado en él, que es transversal a \( Q \), ver Figura 4.a. Estas nuevas líneas son las líneas tangentes a \( C_Q \) en los vértices y se denotarán con la letra minúscula correspondiente. El haz armónico del cuadrilátero \( a, c, b, d \) se llama haz tangente de \( C_Q \) y se denotará \( C^*_Q \).

Figura 4: a) Tangentes de la curva armónica \( C_Q \) en los vértices. b) Punto genérico en la curva armónica \( C_Q \).
Ahora consideremos un punto \( Z \in C_Q \) diferente de los vértices, lo llamamos genérico, ver Figura 4.b. Por definición, las cuatro líneas desde \( Z \) hacia los vértices forman un haz armónico centrado en \( Z \). Sea \( X = (A \vee B) \wedge (C \vee Z) \) y \( Y = (A \vee B) \wedge (D \vee Z) \). Entonces, \( A, X, B, Y \) es un conjunto armónico.
Por lo tanto, podemos recuperar \( Z \) a partir de \( X \in A \vee B \) definiendo
$$ Y = X \cdot \rho_{A,B} \text{ y } Z = (C \vee X) \wedge (D \vee Y). $$
Esto tiene sentido para \( X \) recorriendo todo \( A \vee B \), lo cual genera los cuatro vértices (en un conjunto armónico), de modo que \( C_Q \) está parametrizada por \( X \in (A \vee B) \) a través de esta construcción. Llamamos a esto la construcción HC.
Los puntos en la curva armónica \( C_Q \) están emparejados (es decir, en correspondencia biyectiva) por incidencia con las líneas en su haz tangente \( C^*_Q \).
Prueba. Continuemos con la notación anterior, de modo que \( a, c, b, d \) es el cuadrilátero cuyo haz armónico es \( C^*_Q \). Como antes, estas cuatro líneas generadoras pertenecen al haz porque el vértice al cual son tangentes (llamado su punto de contacto) puede obtenerse como el cuarto armónico de su intersección con las otras tres líneas (ver Figura 4.a). Continuando con la construcción HC y dualizándola (ver Figura 5): sea \( Q = a \wedge b \), \( x = Q \vee Y \) y \( y = Q \vee X \), de modo que \( a, x, b, y \) es en general un haz armónico centrado en \( Q \). Entonces, \( z = (c \wedge x) \vee (d \wedge y) \) es una línea del haz \( C^*_Q \), y cualquier línea de este tipo se expresa de forma única de esta manera.

Figura 5: Incidencia de puntos en una curva armónica y líneas en su haz tangente.
Una polaridad en el plano (en el espacio) es una correspondencia biyectiva entre puntos y líneas (planos) que preserva la incidencia; los términos polar de un punto, polo de una línea (plano) o par polar se utilizan6.
Una curva armónica \( C \) induce una polaridad (expresada mediante letras mayúsculas y minúsculas de la misma letra) que satisface:
Ya hemos visto una parte del ítem (i) como el Lema 2 porque las líneas tangentes a los puntos en una curva armónica se definen como sus líneas polares. El resto de la prueba se dará en la siguiente sección como una consecuencia de un análogo en 3D, el Teorema 4. Por el momento, hagamos dos observaciones sobre este teorema y, asumiendo que es cierto, exploremos algunas de sus profundas consecuencias.
Los dos matemáticos que dieron origen a este teorema son Jean-Victor Poncelet (1788-1867) y Karl G. C. von Staudt (1798-1867). Poncelet demostró la relación de polos y polares para las secciones cónicas usando la armonicidad (en su versión métrica), y poco después, von Staudt desarrolló las polaridades como un concepto general y lo utilizó como una forma alternativa de definir curvas cónicas dentro de la geometría proyectiva sin consideraciones métricas o algebraicas [13]. Esta definición vía polaridades es la que utiliza Coxeter en su influyente libro [4], y la llama “extraordinariamente natural y simétrica” porque tiene la dualidad integrada en ella. En general, existen dos tipos de polaridades: euclidiana, en la cual ningún punto es incidente con su línea polar, e hiperbólica, cuando existen pares de polo y polar incidentes. Los términos utilizados están relacionados con los grupos generados por reflexiones armónicas de pares polares no incidentes. Así, la definición de von Staudt de una curva cónica es equivalente al ítem (i) del teorema para una polaridad hiperbólica, mientras que los resultados de Poncelet pueden reformularse como el ítem (ii).
Como ejemplos de pares polares, hemos nombrado líneas y puntos en la Figura 5 de acuerdo con la regla de mayúsculas y minúsculas para polos y polares con respecto a la curva armónica mostrada \( C_Q \). De hecho, un punto \( Z \in C_Q \) y la línea correspondiente \( z \in C^*_Q \) descrita en el Lema 2 constituyen un par polar que satisface (i).
Dada una polaridad en el plano, sea \( C \) el conjunto de puntos que son incidentes con su línea polar y suponga que el ítem (ii) del Teorema 2 se cumple. Si cada línea se encuentra con \( C \) en a lo sumo dos puntos y \( C \) contiene al menos tres puntos, entonces \( C \) es una curva armónica.
Prueba. Sean \( A, B, C \in C \) tres puntos. Por la hipótesis sobre las líneas, no son colineales. Sean \( a, b \) las líneas polares respectivas de \( A, B \), de modo que \( A \in a \) y \( B \in b \). Sea \( Q = a \wedge b \); es el polo de \( q = A \vee B \) porque las polaridades preservan la incidencia, lo que también implica que \( Q \notin q \). Finalmente, sea \( Q \) el cuadrángulo \( A, C, B, D = C \cdot \rho_{Q,q} \). Para concluir la prueba mostramos que \( C = C_Q \).
Dado \( X \in q \setminus \{A, B\} \), su polar, \( x \), es una línea a través de \( Q \) distinta de \( a \) y \( b \). Sea \( Y = x \wedge q \). Entonces, como \( \rho_{X,x} \) deja \( q \) y \( C \) invariantes y \( q \cap C = \{A, B\} \), transpone \( A \) y \( B \), de modo que \( X, A, Y, B \) es un conjunto armónico. Dado que la polaridad satisface (ii) del Teorema 2, \( C \cdot \rho_{X,x} \in C \), por lo que la construcción A implica que \( C_Q \subset C \). Finalmente, dado \( Z \in C \) distinto de \( A, B, C \), sea \( X = (Z \vee C) \wedge q \), entonces \( Z = C \cdot \rho_{X,x} \) porque la línea \( Z \vee C \) no tiene ningún punto en \( C \) aparte de \( Z \) y \( C \) por hipótesis. Por lo tanto, \( C_Q = C \).
Como corolario de la prueba de este lema (y asumiendo el Teorema de la Polaridad), ahora podemos decir qué cuadrángulos \( Q \) inscritos en una curva armónica \( C \) la generan como su curva armónica, es decir, son tales que \( C_Q = C \). Precisamente aquellos en los cuales el polo de una línea diagonal yace en la otra diagonal. Además, para cualquier trío de puntos \( A, C, B \) (con \( C \) distinguido) en \( C \), tenemos tal cuadrángulo \( A, C, B, D = C \cdot \rho_{(a \wedge b),(A \vee B)} \).
La semejanza abstracta de estos hechos con la construcción del cuarto armónico y la existencia de conjuntos armónicos en la línea proyectiva nos lleva al teorema que se enuncia y prueba a continuación. También debemos señalar que está profundamente relacionado con el modelo proyectivo del plano hiperbólico debido a Beltrami y Klein, el cual utilizó como un ejemplo importante para su Programa de Erlangen, [9].
Si fijamos una curva armónica \( C \), cualquier par de puntos \( A, B \) en \( C \) define una línea hiperbólica \( q = A \vee B \) y una reflexión hiperbólica \( \eta_q = \rho_{Q,q} \) donde \( Q \) es el polo de \( q \).
Entonces, tenemos un subgrupo \( \text{Hyp}(2) \) de \( \text{Har}(2) \), llamado el grupo hiperbólico, el cual es generado por todas las reflexiones hiperbólicas \( \eta_q \) sobre líneas hiperbólicas. Este grupo actúa en el interior de la curva armónica \( C \), la cual se toma como el plano hiperbólico para el modelo.
\( \text{Hyp}(2) \cong \text{Har}(1) \).
Prueba. Primero, definimos el mapa tangencial de \( C \) a una línea tangente, ver Figura 6.a. Sea \( T \) un punto en \( C \) y sea \( t \) su línea tangente (o polar). Para cada \( X \in C \) distinto de \( T \), sea \( X' = t \wedge x \), donde \( x \) es la línea tangente a \( C \) en \( X \). Tomando \( T = T' \), esto da una correspondencia biyectiva \( X \leftrightarrow X' \) entre \( C \) y \( t \), ya que \( x' \) (la polar de \( X' \in t \)) corta a \( C \) en \( T \) y \( X \) para \( X' \neq T \), ver Figura 6.a.
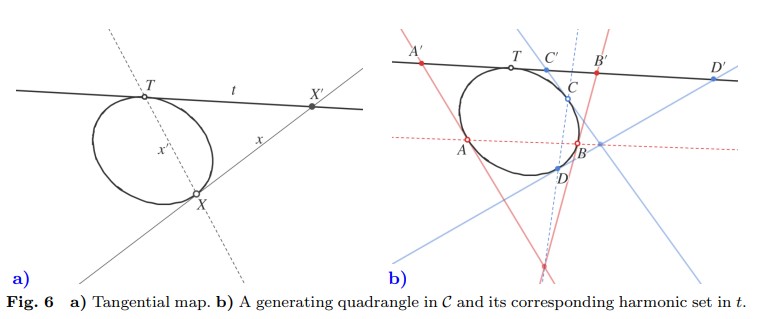
Figura 6: a) Mapa tangencial. b) Un cuadrángulo generador en \( C \) y su conjunto armónico correspondiente en \( t \).
Considerando \( t \) como \( P^1 \), el teorema se deduce del hecho de que los cuadrángulos generadores de \( C \) y los conjuntos armónicos de \( t \) corresponden entre sí, ya que entonces las reflexiones armónicas y las reflexiones hiperbólicas (los generadores de los grupos) corresponden bajo el mapa tangencial.
Sea \( A, C, B, D \) un cuadrángulo generador de \( C \), y sean \( a, c, b, d \) sus respectivas líneas tangentes. Por el Lema 2, el haz armónico de este cuadrilátero es el haz tangente de \( C \) y contiene \( t \). Por lo tanto, según la definición de haces armónicos, tenemos que \( A', C', B', D' \) es un conjunto armónico, ver Figura 6.b.
Esta prueba fue la motivación principal para nuestra definición de curvas armónicas.
La siguiente prueba del Teorema de la Polaridad (Teorema 2) se inspira en la prueba de Dandelin del Teorema Hexagonal de Pascal. Dada una curva cónica, Dandelin construye, en [5], un hiperboloide de revolución que la tiene como una sección plana; luego, usando el hecho de que esta superficie es doble-reglada, obtiene una configuración de 6 líneas en el espacio tridimensional asociadas a los seis puntos del hexágono en la cónica, y argumenta con las propiedades geométrico-combinatorias de la configuración para concluir la prueba. Usamos la misma idea general y llegamos a la misma configuración de 6 líneas, pero en lugar de hiperboloides de revolución, ahora podemos usar superficies regladas generales, siguiendo la construcción de superficies regladas de Hilbert y Cohn-Vossen en [7], que apareció en la imprenta casi un siglo después de la prueba de Dandelin, y aclaró que pueden construirse mediante simples argumentos de incidencia.
Consideremos dos líneas \( a \) y \( b \) en el espacio proyectivo tridimensional. Se tocan si y solo si son coplanares. Si este no es el caso, pueden llamarse un par generador porque para cualquier punto \( X \) que no esté en ellas, existe una única línea a través de \( X \) transversal (es decir, con un punto común) a \( a \) y \( b \); concretamente:
$$ (X \vee a) \wedge (X \vee b). $$
Ahora consideremos tres líneas \( a, b, c \) en posición general (es decir, cada par es generador, o equivalentemente, ningún par de ellas es coplanar). La regla transversal a \( a, b, c \), denotada \( R(a, b, c) \), es el conjunto de líneas que son transversales a ellas (es decir, que tocan a las tres); cualquier conjunto de líneas así se llamará reglado y sus elementos se llaman reglas, ver Figura 7.a. Si denotamos \( R = R(a, b, c) \), la observación anterior implica que \( R \) está parametrizada por incidencia con los puntos en cualquiera de las tres líneas generadoras (por cada punto en ellas pasa una única regla). Es importante señalar que, dualmente, \( R \) también está parametrizada por planos que contienen una de las líneas; si denotamos los planos por letras griegas (puntos y líneas son, respectivamente, letras latinas mayúsculas y minúsculas), tenemos, por ejemplo, que:
$$ R(a, b, c) = \{ (b \wedge \alpha) \vee (c \wedge \alpha) \mid a \subset \alpha \} . $$

Figura 7: a) La regla transversal en líneas azules para tres líneas rojas. b) La regla transversal para tres reglas azules contiene las tres líneas originales rojas.
Cada par de reglas en \( R \) es generador; de lo contrario, sus tres líneas transversales \( a, b, c \) serían coplanares. Por lo tanto, para cualquier trío \( a', b', c' \in R \), obtenemos una regla transversal \( R(a', b', c') \) que contiene las tres líneas originales \( a, b, c \); esta regla es una extensión de \( a, b, c \), ver Figura 7.b. En el espacio proyectivo real, solo existe una extensión para una regla de tres líneas en posición general, pero esto no es cierto en todos los espacios proyectivos. En lo que sigue, asumiremos que nuestro espacio proyectivo tiene esta propiedad, lo cual consideraremos como un axioma:
Tres líneas en posición general pertenecen a una única regla.
Más adelante probaremos que es equivalente al Teorema de Pappus y, por lo tanto, a otras declaraciones clásicas que comúnmente se adoptan como axiomas en geometría proyectiva. Otro nombre para este axioma podría ser el “Axioma de la Doble-Regla” porque implica inmediatamente que las reglas están emparejadas o combinadas: cualquier regla tiene una regla opuesta, que es la regla transversal para cualquiera de las tres de sus reglas. La superficie doble-reglada (también nos referimos a ella simplemente como superficie reglada) obtenida como la unión de las reglas en cualquiera de estas reglas también es la unión de las reglas en su regla opuesta.
Así, cada punto en una superficie reglada tiene un plano tangente, el cual es generado por las reglas únicas a través del punto en las reglas opuestas de la superficie.
El emparejamiento de puntos en una superficie reglada \( S \) con sus planos tangentes se extiende a una polaridad en el espacio proyectivo. Además, si \( P \notin S \), entonces \( P \) no es incidente con su plano polar \( \pi \), y la reflexión armónica \( \rho_{P,\pi} \), con \( P \) como centro y \( \pi \) como espejo, deja \( S \) invariante.
Prueba. La superficie reglada \( S \) tiene dos reglas opuestas \( R \) y \( R' \) tales que:
$$ S = \bigcup_{x \in R} x = \bigcup_{y \in R'} y . $$
Para definir la polaridad inducida por \( S \) en su complemento, fijemos tres reglas \( a, b, c \) en la regla \( R \), y observemos que hemos invertido el uso notacional de los primados: su regla transversal ahora es \( R' = R(a, b, c) \).
Consideremos un punto \( P \notin S \); dualmente, podríamos empezar con un plano no tangente. Sea \( \alpha = a \vee P \). Existe una regla bien definida \( a' \in R' \) tal que \( P \in a \vee a' = \alpha \) (concretamente, \( a' = (b \wedge \alpha) \vee (c \wedge \alpha) \), como en la ecuación anterior). Sea \( A = a \wedge a' \in S \). Observamos que \( A \) debe estar en el plano polar de \( P \) porque las polaridades preservan la incidencia y \( P \) está en el plano polar de \( A \).
De manera análoga, obtenemos \( b', c' \in R' \), para los cuales \( P \in b \vee b' = \beta \) y \( P \in c \vee c' = \gamma \). Sea \( B = b \wedge b' \) y \( C = c \wedge c' \), de modo que el plano polar de \( P \) debe ser:
$$ \pi = A \vee B \vee C . $$
Si hubiéramos comenzado, de manera dual, con un plano no tangente \( \pi \), habríamos encontrado \( P \) como la intersección de los tres planos tangentes en \( A = a \wedge \pi \), \( B = b \wedge \pi \), \( C = c \wedge \pi \); y \( a', b', c' \) serían las reglas en \( R' \) que pasan por \( A, B, C \) respectivamente. Por lo tanto, el emparejamiento de puntos y planos ahora está bien definido.
Hemos distinguido lo que llamaremos una configuración de Dandelin: seis líneas de dos tipos o colores, tres de cada tipo, \( a, b, c \) y \( a', b', c' \)—sin y con primado en el texto, rojas y azules en las ilustraciones, como en la Figura 7.b— tales que un par de ellas se tocan si y solo si tienen tipos opuestos. Esto produce nueve puntos básicos y nueve planos tangentes.
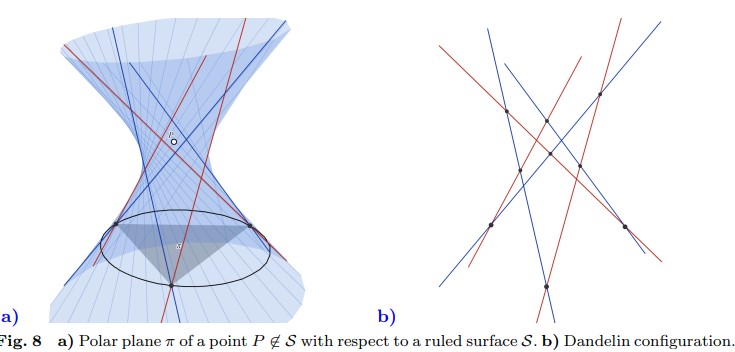
Figura 8: a) Plano polar \( \pi \) de un punto \( P \notin S \) con respecto a una superficie reglada \( S \). b) Configuración de Dandelin.
Los planos tangentes en esta configuración de Dandelin se encuentran por la operación de “unión” (\( \vee \)) o “intersección” (\( \wedge \)) de líneas de diferentes colores, y también producen una configuración derivada de otras líneas y planos que surgen naturalmente de ellas. La riqueza geométrica de esta configuración, estrechamente relacionada con la combinatoria de determinantes \( 3 \times 3 \), es lo que Dandelin explotó en [5]; y seguimos el mismo enfoque.
Ahora, probaremos que la reflexión armónica, \( \rho_{P,\pi} \), con centro \( P \) y espejo \( \pi \), intercambia las líneas \( a, b, c \) respectivamente con \( a', b', c' \) en la regla opuesta. Por la simetría triangular de la construcción, bastará probar que:
Esto ocurre si y solo si \( \rho_{P,\pi} \) intercambia las líneas \( a \) y \( a' \). El plano tangente \( \alpha = a \vee a' \) contiene cinco de los nueve puntos básicos de nuestra configuración de Dandelin. Concretamente, el cuadrángulo \( \alpha \)-:
$$ a \wedge b', b \wedge a', a \wedge c', c \wedge a' , $$
con su centro \( A \) y sus diagonales \( a \) y \( a' \). Los cuatro puntos básicos restantes fuera de \( \alpha \) se dividen naturalmente en dos pares cuyas líneas generadas son incidentes con los dos puntos diagonales del cuadrángulo \( \alpha \). Esto se deduce ya que estos puntos diagonales pueden verse como la intersección de tres planos tangentes. Concretamente, \( P = \alpha \wedge \beta \wedge \gamma \) y \( R = \alpha \wedge (b \vee c') \wedge (c \vee b') = \alpha \wedge (B \vee C) \in \alpha \wedge \pi \) (ver Figura 9).
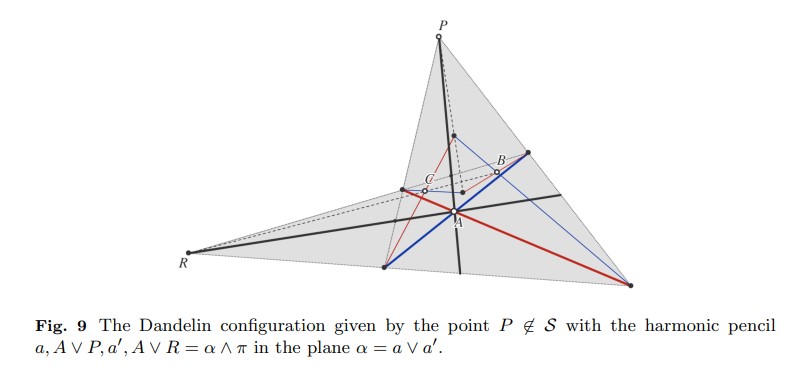
Figura 9: La configuración de Dandelin dada por el punto \( P \notin S \) con el haz armónico \( a, A \vee P, a', A \vee R = \alpha \wedge \pi \) en el plano \( \alpha = a \vee a' \).
Por lo tanto, \( \rho_{P,\pi} \) intercambia las reglas \( a \) y \( a' \). De manera análoga, intercambia \( b \) con \( b' \) y \( c \) con \( c' \). Así, proporciona una biyección entre las reglas transversales de \( a, b, c \) y \( a', b', c' \), que son \( R' \) y \( R \), respectivamente, ya que una línea transversal a \( a, b, c \) es enviada por \( \rho_{P,\pi} \) a una línea transversal a \( a', b', c' \) y viceversa. Por lo tanto, \( \rho_{P,\pi} \) deja \( S \) invariante, como deseábamos probar.
En particular, dado que una reflexión armónica envía una línea a una línea concurrente con el espejo y coplanaria con el centro, nuestra definición de la polaridad no depende de la elección de las reglas generadoras \( a, b, c \).
Finalmente, la prueba de que la polaridad que hemos definido preserva la incidencia sigue en varios casos, pero de manera directa, partiendo del hecho de que si el plano tangente a un punto en \( S \), digamos \( A \) como se mencionó, contiene un punto que no está en \( S \), digamos \( P \), entonces el plano polar de \( P \) contiene \( A \).
Observemos que, debido a la invarianza de la incidencia, la polaridad se extiende naturalmente a un emparejamiento de líneas. El polar de una línea \( \ell \) es la intersección de todos los planos polares de sus puntos, o de cualquiera de dos de ellos.
Este teorema de polaridad afirma que lo que uno ve como el contorno de una superficie reglada es exactamente su sección con el plano polar del punto de vista. Las secciones y el contorno de proyecciones coinciden. Ahora probaremos que las secciones de superficies regladas son curvas armónicas y que el haz armónico correspondiente es la proyección desde el polo de cualquiera de las dos reglas.
Consideremos una curva armónica, \( C \), en un plano \( \pi \). Nuestro objetivo básico es probar que:
es decir, tal que \( C = S \cap \pi \). Esto inducirá la polaridad deseada en \( \pi \) para completar la prueba del teorema.
Por definición, \( C \) es la curva armónica de un cuadrángulo \( A, C, B, D \). Sean \( a \) y \( b \) las tangentes en \( A \) y \( B \), respectivamente; y sea \( Q = a \wedge b \), \( q = A \vee B \). Sabemos que \( D = C \cdot \rho_{Q,q} \) y que \( C \) se obtiene mediante la construcción \( A \)- (2).
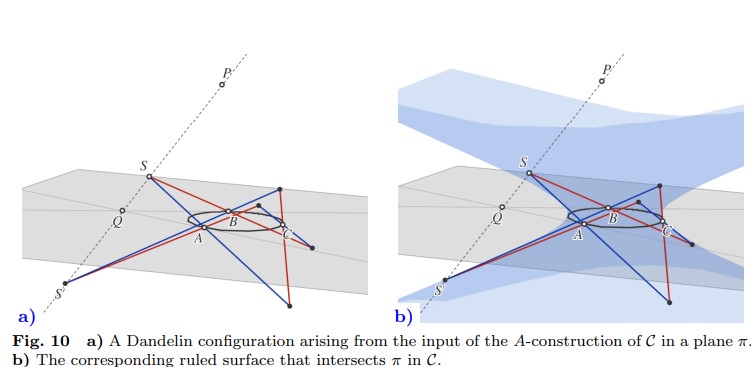
Figura 10: a) Configuración de Dandelin que surge de la construcción A de \( C \) en un plano \( \pi \). b) La superficie reglada correspondiente que intersecta \( \pi \) en \( C \).
El Teorema 5 establece que las curvas armónicas son las secciones de superficies regladas con planos no tangentes. Además, los haces armónicos son la proyección de las reglas desde puntos externos, y el haz tangente de una sección de una superficie reglada es la proyección desde el correspondiente polo de cualquiera de sus dos reglas.
El Axioma Equipolar es equivalente al Teorema de Pappus.
Prueba. Primero, debemos enunciar el Teorema de Pappus:
Sean \( a_0 \) y \( b_0 \) líneas coplanares con puntos \( B_1, B_2, B_3 \in a_0 \) y \( A_1, A_2, A_3 \in b_0 \), de modo que el hexágono de la hipótesis de Pappus es \( A_1, B_2, A_3, B_1, A_2, B_3 \), considerado cíclicamente, y el teorema afirma que los tres “puntos de Pappus”:
$$ P_i = (A_j \vee B_k) \wedge (A_k \vee B_j), $$
donde \( \{i, j, k\} = \{1, 2, 3\} \), son colineales.
La hipótesis del Teorema de Pascal es que los seis puntos mencionados no están en dos líneas, sino en una curva armónica, y la conclusión es exactamente la misma. La prueba original de Dandelin del Teorema del Hexágono de Pascal inspiró nuestro tratamiento y se hace referencia a ella para complementar nuestra presentación.
Prueba (continuación del Teorema de Pappus): La prueba considera reglas (\( a_i \) y \( b_i \), \( i = 1, 2, 3 \)) que pasan por los vértices alternadamente en las dos regulaciones de una superficie reglada. En el caso de Pascal, esto se sigue inmediatamente del Teorema 5; para Pappus, necesitamos trabajar un poco más porque el plano \( \pi = a_0 \vee b_0 \) resultará ser un plano tangente.
Sea \( a_1, a_2 \) un par de líneas generadoras que se encuentran en \( \pi \) en \( A_1, A_2 \) respectivamente. Sea \( R' = R(a_0, a_1, a_2) \) de modo que \( b_0 \in R' \) y sea \( b_1, b_2, b_3 \in R' \) las reglas que pasan por \( B_1, B_2, B_3 \), respectivamente. Ahora, sea \( R = R(b_0, b_1, b_2) \) de modo que \( a_0, a_1, a_2 \in R \), y finalmente, sea \( a_3 \in R \) la regla que pasa por \( A_3 \in b_0 \).
Hemos definido ocho líneas de dos tipos o colores, \( a_i \) y \( b_j \) con \( 0 \leq i, j \leq 3 \), de modo que todos los pares de colores diferentes, excepto uno, se encuentran; específicamente, \( a_i \) se encuentra con \( b_j \) para todos los \( i \neq 3 \neq j \). El Axioma Equipolar implica que \( R = R(b_0, b_1, b_3) \) y, por lo tanto, que \( a_3 \in R \) se encuentra con \( b_3 \). Además, el Axioma Equipolar sigue si esto siempre es cierto para esta configuración general de ocho líneas, ya que implica que \( R = R(b_0, b_1, b_3) \) permitiendo que \( a_3 \) recorra toda \( R \); y luego, moviendo los \( b_j \) alrededor de \( R' \), esto implica que \( a_0, a_1, a_2 \) se extienden a la única regulación \( R \).
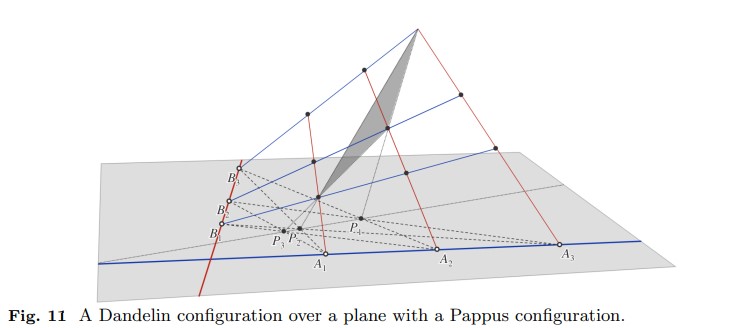
Figura 11: Configuración de Dandelin sobre un plano con una configuración de Pappus.
Nos queda probar que los puntos de Pappus \( P_1, P_2, P_3 \) son colineales si y solo si \( a_3 \) y \( b_3 \) se encuentran, ver Figura 11.
Supongamos que \( a_3 \) y \( b_3 \) se encuentran. Entonces \( a_i \) y \( b_j \), con \( i, j \in \{1, 2, 3\} \), forman una configuración de Dandelin. Para cualquier \( i, j \), tenemos que:
$$ A_i \vee B_j = (a_i \vee b_j) \wedge \pi . $$
De modo que los puntos de Pappus pueden verse como líneas que se intersecan en \( \pi \):
$$ P_i = ((a_j \vee b_k) \wedge (a_k \vee b_j)) \wedge \pi = ((a_j \wedge b_j) \vee (a_k \wedge b_k)) \wedge \pi , $$
para \( \{i, j, k\} = \{1, 2, 3\} \). Como estas tres líneas se encuentran por pares, están contenidas en un plano que define la línea de Pappus:
$$ p = ((a_1 \wedge b_1) \vee (a_2 \wedge b_2) \vee (a_3 \wedge b_3)) \wedge \pi , $$
lo que prueba el Teorema de Pappus y, para planos no tangentes \( \pi \), constituye la prueba de Dandelin del Teorema de Pascal.
Nos queda probar que el Teorema de Pappus implica el Axioma Equipolar, lo cual, como hemos visto, se sigue de probar que \( a_3 \) se encuentra con \( b_3 \) suponiendo que \( P_1, P_2, P_3 \) están en una línea \( p \subset \pi \). Observe que la ecuación (4) aún se cumple para \( i = 3 \) (y \( \{j, k\} = \{1, 2\} \)), de modo que:
$$ \delta = p \vee ((a_1 \wedge b_1) \vee (a_2 \wedge b_2)) $$
es un plano porque las dos líneas se encuentran en \( P_3 \). Contiene las líneas:
$$ \ell_1 = P_1 \vee (a_2 \wedge b_2) \text{ y } \ell_2 = P_2 \vee (a_1 \wedge b_1) , $$
que nos dan un punto \( W = \ell_1 \wedge \ell_2 \). Para ver que \( W \in a_3 \) y \( W \in b_3 \) para concluir la prueba, observe que \( W \) puede verse como la intersección de tres planos en dos formas: a saber, de \( \delta \), \( (a_3 \vee b_1) \), \( (a_3 \vee b_2) \) y \( \delta \), \( (a_1 \vee b_3) \), \( (a_2 \vee b_3) \).
Lo que hemos hecho en este artículo funciona literalmente en el contexto abstracto de la geometría proyectiva. Las imágenes incluidas, diseñadas para ayudar al lector a comprender intuitivamente los argumentos abstractos, están dibujadas en espacios euclidianos de 2 y 3 dimensiones. Sin embargo, no se utilizan argumentos euclidianos, excepto en algunas declaraciones, como al mostrar que las curvas armónicas son secciones cónicas y para el modelo del plano hiperbólico (¡el plano, no el grupo!). Dado que la Geometría Proyectiva siempre ha sido terreno para consideraciones sobre los fundamentos de las matemáticas, creemos que es apropiado cerrar con algunas observaciones sobre la axiomatización y el contenido matemático riguroso de nuestras pruebas.
Los axiomas en los que se basa nuestra presentación y sobre los cuales están probados todos sus teoremas son los siguientes. Un espacio proyectivo consiste en un conjunto base o espacio de puntos con una familia bien definida de subconjuntos llamados líneas, que satisfacen:
Estos axiomas son una variación de los comúnmente utilizados (por ejemplo, los sugeridos por Stillwell en [11]). La principal diferencia es la sustitución del Teorema de Pappus por el Axioma Equipolar (o de Doble-Regulación). Los axiomas 1 y 2 son los axiomas de incidencia fundamentales. La declaración del Axioma 2 se atribuye a Pash y Veblen; describe que dos líneas se encuentran si y solo si son coplanares sin necesidad de definir previamente los planos. El Axioma 3 significa que el espacio es al menos tridimensional y se sabe que es equivalente al Teorema de Desargues. El Axioma 4 es necesario para que la geometría sea interesante y no se reduzca a una teoría de conjuntos trivializada.
Los dos axiomas finales dependen de un desarrollo adicional de la teoría; no son primitivos. El Axioma 5 garantiza que el campo base tiene una característica distinta de 2, o equivalentemente, que la geometría no contiene el Plano de Fano. La característica de un espacio proyectivo puede definirse geométricamente utilizando la construcción del cuarto armónico; esencialmente, en función de cuánto se puede avanzar en una secuencia armónica sin retornar. Esto es necesario aquí para dar sentido a las curvas armónicas (y que las reflexiones armónicas no sean la identidad), porque implica que existen conjuntos armónicos de exactamente cuatro puntos. El Axioma 6 es un principio adicional requerido para que la geometría sea lo suficientemente rica como para tener una relación profunda con otras ramas clásicas de las matemáticas, como el análisis y la topología; más adelante, discutiremos las varias versiones que puede adoptar.
A partir de los primeros cuatro axiomas, se pueden definir las variedades como subconjuntos cerrados bajo la operación de tomar líneas, y luego, la dimensión de una variedad se obtiene como uno menos que el número de puntos necesarios para generarla; así, los planos se definen como variedades de dimensión 2 [12]. Las propiedades de incidencia de planos y líneas en un espacio de dimensión 3 se obtienen a partir de esto; y la construcción de superficies regladas de Hilbert-Cohn Vossen se sigue, dando sentido a la declaración del Axioma Equipolar.
Dado que el Axioma Equipolar es equivalente al Teorema de Pappus, la aritmetización del espacio proyectivo produce un campo base conmutativo. En [11] se demuestra la conmutatividad a partir del Teorema de Pappus y se describe el campo base desde cero. La necesidad del axioma se prueba construyendo un espacio proyectivo sobre un campo no conmutativo, como los cuaterniones.
Otra versión ampliamente utilizada del Axioma 6 es como la parte de unicidad del Teorema Fundamental de la Geometría Proyectiva. Generalmente se enuncia en el contexto de la geometría plana, donde los Axiomas 1 y 2 se vuelven duales de manera atractiva (y el Axioma 3 es falso, pero se reemplaza por el Teorema de Desargues). Una proyectividad se define como la composición de proyecciones entre puntos en líneas o líneas en haces concurrentes; siempre son biyecciones. No es difícil construir una proyectividad determinada por su efecto en tres elementos arbitrarios de su dominio. Esta es la parte de existencia del Teorema Fundamental. Sin embargo, la unicidad se demuestra como equivalente al Teorema de Pappus, por lo que uno debe asumirse para probar el otro, ver [4], [12].
Creemos que el Axioma 3 es natural porque, entre otras cosas, responde y da crédito a la motivación original para la creación de la Geometría Proyectiva, que es la perspectiva renacentista, para la cual la dimensión 3 es esencial. Pero luego, si se considera la proyectividad entre líneas no coplanares en un espacio proyectivo tridimensional, uno se lleva naturalmente a considerar superficies regladas. De hecho, dada una proyectividad de una línea \( a \) a una línea no coplanar \( b \), el conjunto de líneas que unen un punto en \( a \) con su imagen en \( b \) resulta ser una regulación. Por lo tanto, el Axioma Equipolar está íntimamente relacionado con la unicidad de las proyectividades dadas por tres valores arbitrarios (la proyectividad está determinada por la regulación extendida de tres líneas). Además, esta asociación de un conjunto de líneas con una transformación entre líneas es también una idea clásica. Es el dual de cómo Jakob Steiner (1796–1863) definió las curvas cónicas de manera puramente proyectiva; y es una forma visual y natural de presentarlas, ver, por ejemplo, [12].
El sistema de proyecciones, dualidades, polaridades, conjuntos armónicos y reflejos armónicos en el contexto de la geometría proyectiva no solo representa un conjunto completo de herramientas y conceptos que enriquecen la geometría, sino que también antecede casi en un siglo a la noción de conjuntos y el lenguaje de funciones abstractas; además, en conjunto, constituyen lo que ahora llamamos un grupoide (definido a mediados del siglo XX en la teoría de categorías). Y, por supuesto, tuvo un rol fundamental en la ampliación de nuestra noción de geometría y su influencia en los albores de la topología. Existen muchas maneras de abordarlo y presentarlo. Esperamos que este artículo contribuya a la conciencia de su importancia cultural y la conveniencia y posibilidad de acercarlo “a las escuelas secundarias” [8], o al menos a los primeros cursos universitarios.
J. Bracho agradece el apoyo del Proyecto PAPIIT-UNAM IN109023.