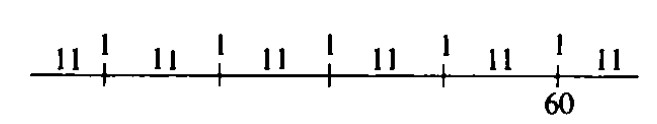(a) Se observan números aleatorios en locomotoras en orden, 1, 2, ... N. Un día ves una locomotora y su número es 60. Adivina cuántas locomotoras tiene la compañía.
(b) Has visto 5 locomotoras y el número más alto observado es 60. Adivina nuevamente cuántas locomotoras tiene la compañía.

Discusión para el Problema de las Locomotoras

Aunque la pregunta tal como está planteada no proporciona "respuestas correctas", todavía hay algunas cosas razonables que hacer. Por ejemplo, el principio de simetría sugiere que cuando se elimina un punto, en promedio los números más grandes serán de igual tamaño que los menores, por lo que podría estimar en la parte (a) que el número es 119, porque el segmento a la izquierda de 60 tiene 59,

\(2 \times 59 = 118\),

y 118 + 1 = 119.

De manera similar en la parte (b), podría estimar que los 5 números observados dividen la serie completa en 6 piezas. Como 60 - 5 = 55, el promedio

la longitud de las 5 piezas es 11, y por lo que podría estimar el número total como 60 + 11 o 71. Por supuesto, no puede esperar que su estimación sea exacta muy a menudo.

El método descrito justo antes asegura que en muchas de tales estimaciones se acerque a la estimación correcta en promedio. Es decir, imagine muchos problemas en los que se debe adivinar el número desconocido N. Siga el procedimiento de estimación anterior. Luego tome la muestra (haga una estimación). Entonces el conjunto de estimaciones en promedio estará cerca del valor verdadero a largo plazo.

Por otro lado, puede que no le interese estar en lo cierto a largo plazo en promedio, sino cada vez.

Podría querer intentar estar exactamente en lo cierto en esta ocasión, sin embargo, la esperanza puede fallar. Entonces una estrategia razonable es simplemente adivinar como N el número más grande que ha visto. Si ha visto 2 locomotoras, entonces la probabilidad de que una de ellas sea el número N \[ \frac{N-1}{\binom{N}{2}} \text{ o } \frac{2}{N} \] 

El método de confianza también se usa a menudo para hacer una estimación de intervalo. Para una descripción, hablaré del caso de una observación.  Si la compañía tiene N locomotoras y sacamos una al azar, entonces la probabilidad de que los números 1, 2, ..., N de que saquemos uno n y sea igual a N es 1/N.

Por ejemplo, deje que n sea el número aleatorio a extraer, entonces para valores de N par, \(P(n > N/2) = \frac{1}{2}\) y para valores de N impar la probabilidad es ligeramente mayor. Entonces podemos leer esto como sigue: la probabilidad de que N sea menor que 2n es al menos la mitad, y si decimos que N es menor que 2n, esto  es verdadero con probabilidad al menos  1/2.

Si no conocemos el valor de N debemos decir que N es menor o igual a 2n.

Supongamos que decimos que N es menor que 3n,

P(n>N/3) = 2/3

En nuestro problema, diremos que N es menor que 180 con una probabilidad de acierto de al menos 2/3.

P(n<2N/3)=2/3,

luego N>3n/2 con probabilidad 2/3.

Podríamos también decir que N es mayor que 90 con probabilidad de acertar 2/3. Pero N está entre 90 y 180 con probabilidad 1/3.

Otro método de estimación que está de moda, al momento de escribir el libro, es la estimación de máxima verosimilitud. Que elige el valor de N que maximiza la probabilidad P(n/N). Se elegiría el valor de N que hace que nuestra muestra sea más probable .Así si  N fuera 100, la probabilidad de n=60 es 1/100 , si N fuera 60, la probabilidad de ver 60 es 1/60. La probabilidad de que salga 60 si N es 59 o menos será 0.
En consecuencia la estimación de máxima verosimilitud de N es \(n\).

En esta discusión no se ha intentado usar información casual como "es una gran compañía , por lo tanto debe tener al menos 100 locomotoras , pero no podría tener 100000 ." Esa información puede ser útil.

A continuación hemos realizado con ayuda de ChatGpt una escena en la que se ve un número N aleatorio y utilizamos según cada observación el método 1 (simetría) o el método 2 (confianza)
El método 2 no lleva memoria de lo que ocurre en una observación anterior.

método 1 con la primera observación dice N1=(O_1-1)*2/1+1 con la segunda observación dice N1=(max(O_1, O_2)-2)*3/2+2 con la 3ª observación dice N1=(max(O_1, O_2, O_3)-3)*4/3+3 ... con la iª observación dice Ni=ent((max(O_1, ..., O_i)-3)*(n+1)/n+n)

método 2 con la 1ª observación dice N2=3*O_1 con la 2ª observación dice N2=3*O_2 ... con la iª observación dice Ni=3*O_i

el error1  es |N-N1|/N,  error2 que es |N-N2)/N|