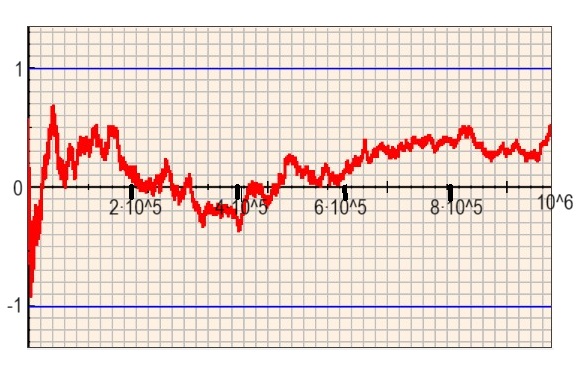
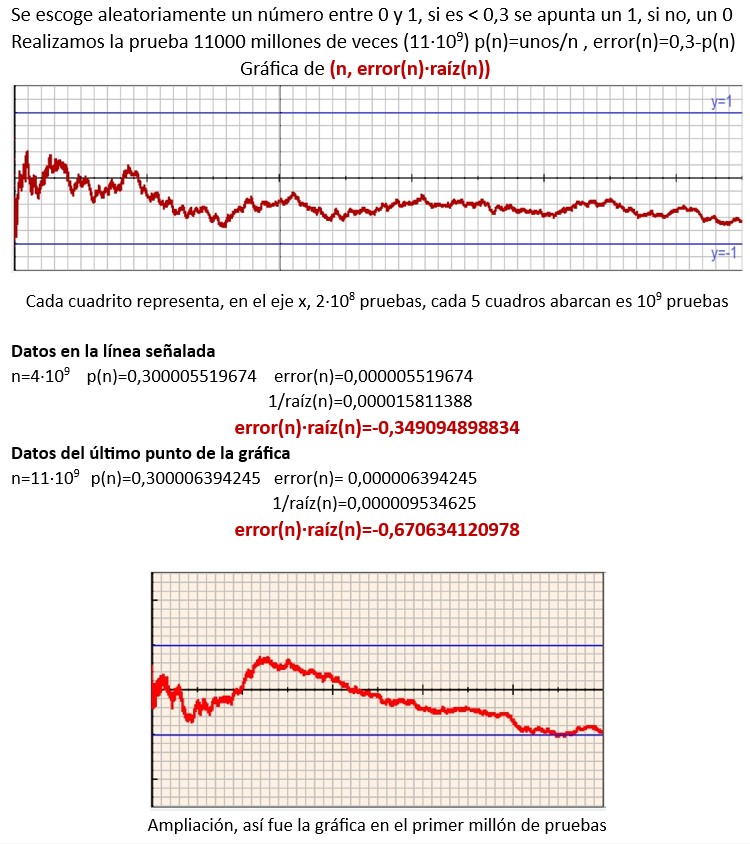
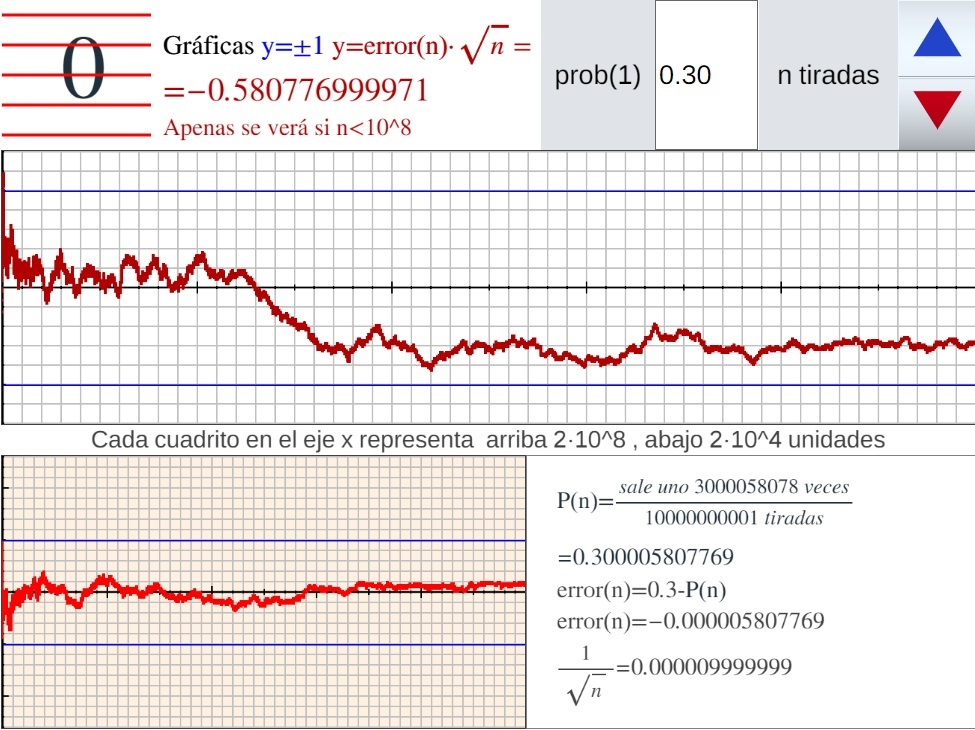
Error vs 1/raíz(n) Tirar una moneda con probabilidad de cara 0.3   Lanzamos una moneda y apuntamos las veces que sale cara .En el experimento se pretende estudiar la función error(n)=0.3-P(n) y compararla con 1/raíz(n). P(n) es el número de veces que salió cara entre el número n de lanzamientos realizados. ¿Por qué esta comparación? Pues esta comparación nos puede ayudar a escoger el tamaño de la muestra en un experimento según la aproximación deseada. Así si nos basta con porcentajes, error(n) < 0,01 y admitiéramos que  |error|<1/raíz(n) sabríamos que para un error menor que 0,01 , nos bastaría con una muestra de tamaño 10000 Para esta comparación se ha creado una escena de Descartes que en lugar de lanzar una moneda escoge un número entre 0 y 1, si el número es menor que 0.3 anotamos un 1, en caso contrario, un 0. La escena dibuja la gráfica de error(n) · raíz(n) Hemos realizado 10^10 lanzamientos (tiradas) obteniendo estas gráficas de error(n) · raíz(n) En esta imagen solo se van recogiendo los puntos cuya n es múltiplo de 10000 La gráfica de los primeros 10^6 lanzamientos ha sido En esta imagen se han dibujado todos los puntos para n menor que 10^6   La gráfica desde el lanzamiento 6000 al 6001 millones fue Aquí se dibujan todos los puntos de la gráfica para n desde 6000 millones hasta 6001 millones.   Datos con n=10^6 P(n)=0.299491 error(n)=0.000508999999 raíz(n)=1000   1/raíz(n)=0.001 error(n)·raíz(n)=0.508999999999   Datos con n=10^10 P(n)=0.2999967412 error(n)=0.000003258799 raíz(n)=10^5    1/raíz(n)=0.00001 error(n)·raíz(n)=0.325879999996     La escena con la que se ha realizado el experimento es la siguiente. Cada vez que se pulsa uel triángulo azul (esquina superior derecha) se realizan 10^4 tiradas. Este valor se puede modificar: con clic derecho en la escena salen más controles para realizar cambios.     Pondremos las capturas de algún experimento más   Consolación Ruiz Gil Enero 2024  https://www.matsolin.com/monedas/index.htm