|
El Problema de Monty Hall Una Decisión EstratégicaEl enigma del Problema de Monty Hall toma su nombre del conocido presentador del programa "Let’s Make a Deal" (Hagamos un trato) de la televisión estadounidense. En este juego, se presentan tres puertas, detrás de una de las cuales se esconde un valioso premio, como un coche, mientras que las otras dos contienen cabras. El participante elige inicialmente una puerta, y luego el presentador revela una de las puertas restantes que contiene una cabra. La pregunta clave que surge es: ¿debería el participante mantener su elección inicial o cambiar de puerta para aumentar sus posibilidades de ganar el premio principal, el coche? La respuesta a este enigma aparentemente sencillo es sorprendentemente controvertida y depende de varios factores, como si el presentador sabe lo que hay detrás de cada puerta o si su elección fue aleatoria. En esta página, exploraremos en detalle ambos escenarios y analizaremos las estrategias óptimas para maximizar las probabilidades de ganar el deseado premio.
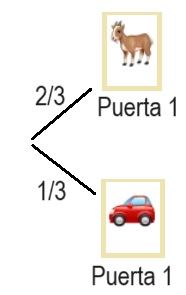
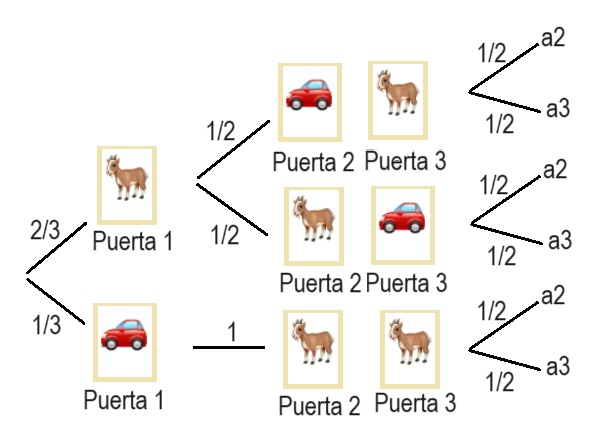
Solución Planteemos el problema paso a paso en forma de árbol El concursante eligió la puerta 1, las posibilidades de la puerta 1 son dos
Y en cada caso, las posibilidades para las otras puertas son las siguientes
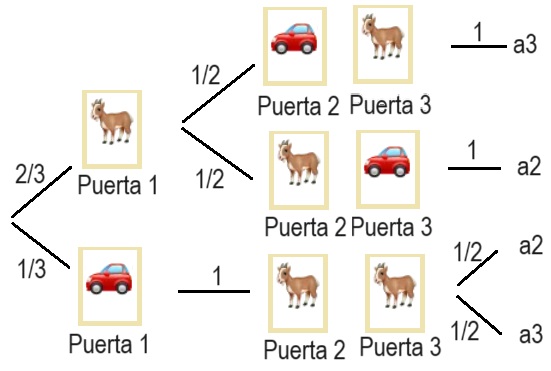
Hasta aquí el problema es igual que en problema 2, pero ahora el presentador que ha visto lo que hay detrás de las puertas abre una que es cabra, designamos por ai el suceso "abre la puerta i"
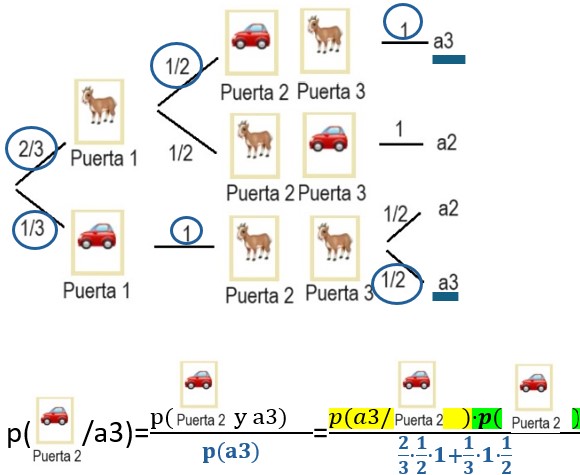
El problema ahora dice que el presentador abrió otra puerta, supongamos que la 3, nos muestra que detrás había una cabra y da la oportunidad al concursante de cambiar de puerta ¿qué debe hacer el concursante? Pues en este árbol tenemos que calcular p(
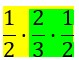
y calculando las probabilidades del numerardor: 1· 2/3·1/2 y operando resulta que p( A continuación se simula el problema de Monty Hall con una escena de Descartes JS
Escena del proyecto ed@d Grupo Descartes
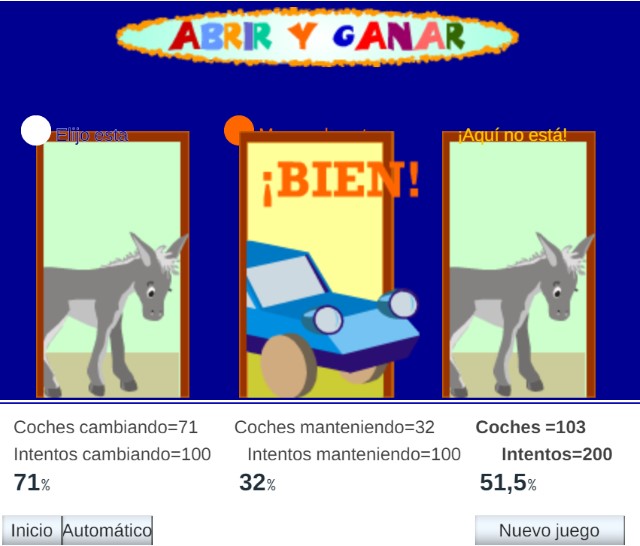
Y esta es una captura del resultado de la escena tras haber realizado la prueba 200 veces, 100 eligiendo el cambio de puerta y 100 manteniendo la escogida en principio
Problema 2 el presentador abre la puerta al tuntún y resulta que había una cabra Solución Planteemos el problema paso a paso en forma de árbol El concursante eligió la puerta 1, las posibilidades de la puerta 1 son dos
Y en cada caso, las posibilidades para las otras puertas son las siguientes
Hasta aquí el problema es igual que en problema 1, pero ahora el presentador sin ver lo que hay detrás de las puertas abre al tuntún una de las otras dos y resultó que tenía cabra, designamos por ai el suceso "abre la puerta i"
El presentador da la oportunidad al concursante de cambiar de puerta ¿qué debe hacer el concursante? Pues en este árbol tenemos que calcular p( Si las calculamos sobre este árbol resulta 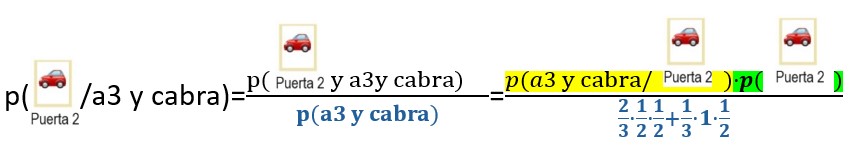
las probabilidades del numerador son Haciendo las operaciones concluimos que p( Y sobre ese mismo árbol es fácil ver que p( Luego si el presentador no ve lo que hay
detrás de las puertas y abre al tuntún una resultando ser cabra,
no aumentarán las probabilidades de ganar el coche cambiándonos
de puerta En la escena se simula este segundo problema, el presentador abre una de las puertas no elegidas al tuntún, a veces abre y muestra el coche. Si jugamos muchas veces veremos que las probabilidades de ganar cambiando de puerta son las mismas que manteniéndonos en la misma puerta.
La siguiente imagen es una captura del resultado obtenido después de múltiples jugadas
En el canal de matemáticas Mates con Andrés está explicado de forma muy sencilla https://www.youtube.com/watch?v=QsWwNbr8G0o
Mates con andrés vídeos de probabilidad Enlace a la escena de la película Black Jack donde se menciona el problema En la serie Numbers también se explica el problema
VAMOS A LIARNOS Con este mismo esquema pensemos en el problema 2
El presentador ahora no ve lo que hay detrás, abrió al tuntún y salió
cabra, utilicemos el esquema si estamos en la posibilidad 1) del esquema, el presentador ha abierto la puerta dos y obtengo el coche si me cambio, en caso de que esté en la posibilidad 2), el presentador ha abierto la tres y yo obtengo premio si me cambio, en caso de que esté en la 3), gano coche si permanezco,
por tanto en dos
de las tres posibilidades al cambiarme tendré el premio. ¿Qué ocurre? Lo que ocurre es que si el presentador abrió y saliò cabra, hay el doble de posibilidades de estar en 3) a estar en 1) y las tres posibilidades que presenta el esquema no son equiprobables, cuando el presentador pudo mostrar coche no son equiproblables. Cuando el presentador ve lo que hay detrás , las tres posibilidades siguen siendo equiprobables pues en cada una es seguro que el presentador muestra cabra. Utilicemos ahora otro argumento para el problema 1
Si el presentador abre la puerta 3 con cabra
no hay más que dos posibilidades, la 2) y la 3) del esquema, luego
puestos en la situación de la puerta abierta tenemos las mismas
posibilidades de ganar manteniéndonos en la puerta 1 o cambiándonos a la
2. Sin duda este es un problema de probabilidad muy bien ideado. En febrero
de 1975, Steve Selvin (n.1941) publicó en la revista trimestral The
American Statistician una carta titulada Un problema de probabilidad, en
ella planteó y resolvió un problema, que conocemos como el Problema de
Monty Hall. La carta levantó algunas críticas tanto por la solución
aportada por Selvin como por lo sorprendente de su resultado. Seis meses
después apareció en la misma revista una carta de seguimiento del autor
titulada Sobre el problema de Monty Hall. En esta carta, Selvin expuso
una solución basada en el teorema de Bayes y explicó algunos detalles
sobre el comportamiento del moderador del concurso. Carta enviada por Selvin a The American Statistician en Feb 1959
En 1959 Martin Gardner publicó este problema de los tres prisioneros , personalmente es la explicación que más me gusta, siempre se asegura de que las posibilidades sean disjuntas y que el total sea el suceso seguro. Así no hay lío que valga.
Consolación Ruiz Gil Febrero 2024 https://www.matsolin.com/monyhall/index.htm
|
||||