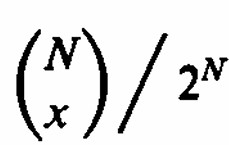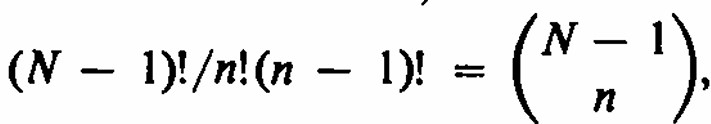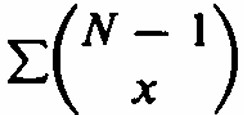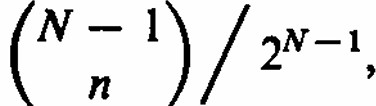Los jugadores A y B juegan a cara o cruz N veces.

Llevan un registro de sus ganancias y pérdidas .

Después del primer lanzamiento , ¿cuál es la probabilidad de que en ningún momento durante el juego estén empatados ?

Solución

A continuación, extendemos el método descrito en la Solución para la Urna Electoral , Problema 22 , para mostrar que la probabilidad de no obtener un empate es, según sea N par o impar, la siguiente:

Las fórmulas muestran que la probabilidad es la misma para un N par y para el siguiente número impar N + 1.

Por ejemplo , cuando N=4 se aplica la fórmula .

Los 16 posibles resultados son

donde la estrella indica que no hay empate. Dado que el número de combinaciones de 4 cosas tomadas 2 a la vez es 6, la fórmula se verifica.

Para N = 2n, la probabilidad de x victorias para A es

Si x≤n, la probabilidad de un empate es

2x/N,

basada en el resultado de la urna electoral,

y para x>n es

2(N − x)/N.

Para obtener la probabilidad incondicional de un empate ponderamos la probabilidad de x victorias por la probabilidad de un empate con x victorias

Cuando los coeficientes binomiales se convierten en factoriales y se cancelan sus coeficientes , encontramos que,  excepto por un término faltante que es

la suma entre corchetes sería

sobre los posibles valores de x .

Consecuentemente , podemos reescribir la expresión ( 1 ) como

El complemento de la expresión ( 2 ) da finalmente la probabilidad de no empate

lo cual se puede escribir con un poco de álgebra

 como se sugirió anteriormente .

Simulación con chatGPT

Simularemos el lanzamiento de M monedas  siendo M par,

las monedas en lugar de cara o cruz se designarán con

+1 y -1

de este modo se producirá un empate cuando la suma de las monedas de la primera a la i-ésima de cero para algún i de 2 a M.

Se calculan los casos o secuencias de monedas de no empate dividido por el número de lanzamientos.