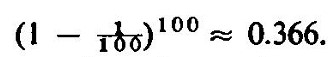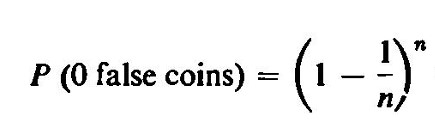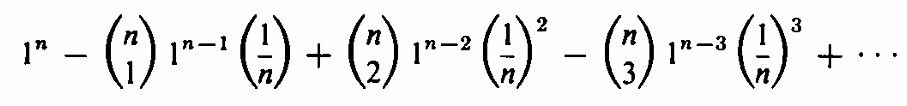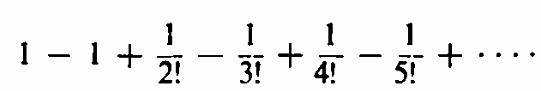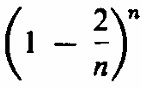( a ) El acuñador del rey guarda sus monedas en cajas de 100. En cada caja pone 1 moneda falsa. El rey sospecha del acuñador y de cada una de las 100 cajas saca una moneda al azar y la hace probar . ¿Cuál es la probabilidad de que las malversaciones del acuñador pasen desapercibidas?

( b ) ¿Qué pasa si ambos 100's son reemplazados por n?

Solución

La probabilidad pedida en (a) es

( b ) Supongamos que hay n cajas y n monedas por caja. Para cualquier caja, la probabilidad de que la moneda sacada sea buena es 1 -1 / n , y dado que hay n cajas,

Veamos esta probabilidad para algunos valores de n

Dos cosas destacan .

Primero , los números en la tabla aumentan ;

y segundo , pueden estar acercándose a algún número .

El número al que se acercan es bien conocido , y es

e - ¹ o 1 / e ,

donde e es la base de los logaritmos naturales , 2.71828 ...

Si expandimos esta probabilidad (1+1/n)ⁿ resulta

o

Si tomamos uno de estos términos , digamos el cuarto , y estudiamos su comportamiento a medida que n se vuelve muy grande , encontramos que se acerca a -1/3 ! porque

A medida que n crece, todos los términos del lado derecho de la ecuación . ( 2 ) excepto el 1 tienden a cero . De manera similar , para el término r de la expansión ( 1 ) los factores que dependen de n tienden a 1, y el término mismo tiende excepto por el signo a 1 / ( r− 1 ) !. Por lo tanto, cuando n crece la probabilidad de que una moneda falsa sea detectada es

Esta serie es una forma de escribir e^-1 

Si hubiéramos investigado el caso de 2 monedas falsas en cada caja, habríamos encontrado que

que al crecer n tiende a e^-2

y en general

que tiende a e^-m

Estos hechos son importantes para nosotros. Se pueden estudiar con más tranquilidad y más rigurosamente en libros de cálculo, por ejemplo, Thomas, G. B., Jr., Elementos de cálculo y geometría analítica, Addison- Wesley, Reading, Mass., 1959, pp. 384–399.

SIMULACIÓN CON CHATGPT

Al pulsar una extracción se saca una moneda de cada caja, si sale roja es la falsa. ND cuenta las extracciones en las que no se detecta ninguna falsa, el falsificador no es pillado, P es la probabilidad que tiene el falsificador de quedar libre.

Créditos
Traducción del problema 27 del libro Fifty challenging problems in probability , MOSTELLER

Vídeo introducción con lumen5.com