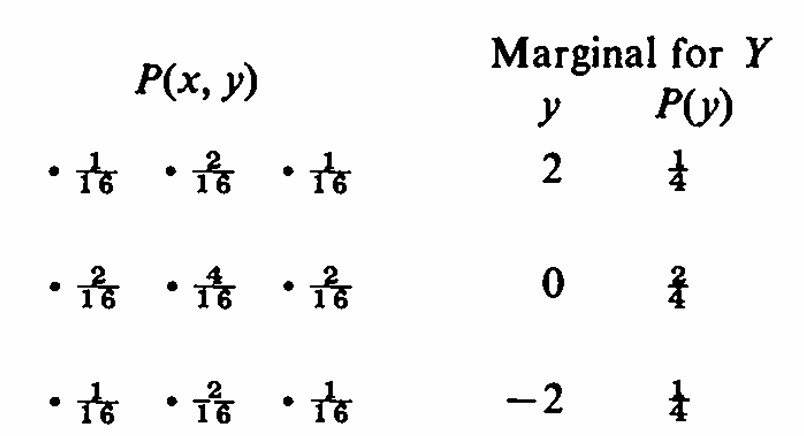51. Paseo Aleatorio en Dos Dimensiones

Partiendo desde un origen \(O\), una partícula tiene una probabilidad de 50-50 de moverse 1 paso al norte o 1 paso al sur, y también una probabilidad de 50-50 de moverse 1 paso al este o 1 paso al oeste. Después de tomar el paso, el movimiento se repite desde la nueva posición y así sucesivamente indefinidamente. ¿Cuál es la probabilidad de que la partícula regrese al origen?

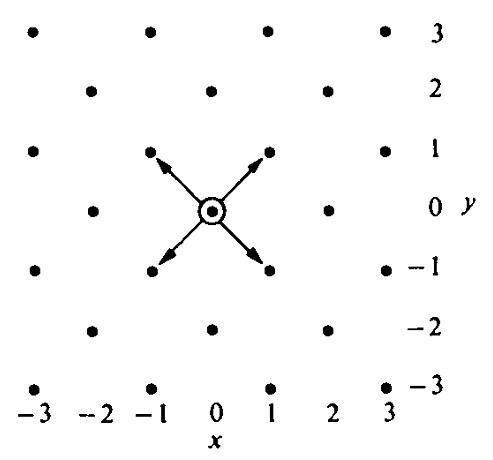
Parte de la red de puntos recorridos por partículas en el problema de paseo aleatorio en dos dimensiones. En cada movimiento la partícula avanza un paso al noreste, noroeste, sureste o suroeste desde su posición actual, siendo igualmente probables todas las direcciones.

Solución para el Paseo Aleatorio en Dos Dimensiones

En el paseo aleatorio unidimensional, The Cliff-Hanger, Problema 35 (último párrafo de la Solución), encontramos que la probabilidad de que la partícula regrese al origen es uno cuando las probabilidades de pasos a la izquierda y a la derecha eran igualmente probables. Pero las cuestiones estaban delicadamente balanceadas. Si la probabilidad hubiera cambiado de \(\frac{1}{2}\), la partícula se habría desviado hacia el infinito. En dos dimensiones uno podría suponer que la partícula tiene mucho espacio para vagar hasta el infinito. Veamos. Planeo encontrar el número promedio de veces que una partícula regresa al origen y, a partir de esto, deducir la probabilidad de que la partícula regrese. Primero, ¿cuántas veces una partícula puede volver al origen? Si \(P\) es la probabilidad de un retorno, entonces \(1 - P = Q\) es la probabilidad de no retorno. La probabilidad de exactamente \(x\) retornos es \(P^x Q\), porque después de cada retorno la partícula podría ser considerada como empezando de nuevo. Si \(P\) fuera conocido, entonces el número promedio de retornos al origen podría calcularse a partir de esta serie geométrica como \[ \mu = \sum_{x=0}^{\infty} x P^x Q. \]

Mirando atrás al Problema 4 sobre pruebas hasta el primer éxito, encontramos que el número promedio es el recíproco de la probabilidad de éxito. En ese problema, el éxito terminaba la serie. Aquí un no-retorno al origen termina la serie, y así el número promedio de pruebas hasta el primer éxito es \(1/Q\). Consecuentemente, el número promedio de éxitos es \(1/Q - 1\). Si \(Q = 1\), entonces el número promedio de éxitos es 0, es decir, con probabilidad uno una partícula se pierde y nunca regresa. Por otro lado, cuanto más pequeño es \(Q\), mayor es el número promedio de retornos. De hecho, por cada \(Q\) hay un número promedio de retornos y para cada promedio hay un \(Q\). Si el número promedio de retornos causa que \(Q\) sea finito, entonces \(P\) es finito. Como \(x\) tiende a \(\infty\), \(P\) tiende a 1. Ahora para

comprender la historia del paseo aleatorio en dos dimensiones, todo lo que necesitamos hacer es calcular \(\mu\).

Partiendo desde el origen, la partícula solo puede regresar al origen en un número par de pasos. Además, su camino puede representarse como el producto de dos paseos aleatorios unidimensionales independientes, cada uno comenzando en cero, uno avanzando al este o al oeste en cada movimiento, el otro avanzando al norte o al sur en cada uno. Por ejemplo, lanza una moneda dos veces; el primer lanzamiento decide el componente este-oeste, el segundo el componente norte-sur. Después de los primeros dos pasos, el componente horizontal, \(X\), tiene la distribución

El componente vertical, \(Y\), se distribuye de manera similar después de dos pasos, y su probabilidad conjunta se distribuye sobre los 9 puntos posibles como sigue:

Marginal para x

La información principal que deseamos notar es que la probabilidad de estar en el origen es \(\frac{4}{16}\) y que se puede obtener multiplicando \(P(X = 0)\) por \(P(Y = 0)\) debido a la independencia de los paseos componentes. Finalmente, queremos interpretar esta información. Al final de dos movimientos \(\frac{4}{16}\) de las partículas han regresado al origen. La contribución al número promedio de retornos al origen es entonces \(\left(\frac{4}{16}\right) + \left(\frac{1}{16}\right)·0 = \frac{4}{16}\). Calculamos la probabilidad de que la partícula esté en el origen después de 2, 4, 6, ... intentos y sumamos estos valores para obtener el número esperado de veces que la partícula regresa al origen.

Después de \(2n\) movimientos, \(n = 1, 2, \ldots\), la probabilidad de que la partícula esté en el origen es \[ P(\text{partícula en el origen}) = P(X = 0)P(Y = 0) = \left(\binom{2n}{n}\left(\frac{1}{2}\right)^{2n}\right)^2, \]

porque debemos obtener números iguales de movimientos hacia el este y el oeste, así como números iguales de movimientos hacia el norte y el sur. (Realmente debería poner subíndices en \(X\) y \(Y\), escribiendo \(X_{2n}\), pero eso hace que la página se vea horrible para mí y atemorizante para algunos). Planeamos sumar, aproximadamente, estas probabilidades para obtener el número esperado de retornos. Para valores grandes de \(n\) podemos aplicar la aproximación de Stirling dada en el Problema 18 y obtener \[ \binom{2n}{n} \left( \frac{1}{2} \right)^{2n} = \frac{(2n)!}{n! \, n!} \left( \frac{1}{2} \right)^{2n} \approx \frac{\sqrt{2\pi (2n)}(2n)^{2n+1/2} e^{-2n}}{(\sqrt{2\pi n} \, n^{n+1/2} e^{-n})^2 2^{2n}} \approx \frac{1}{\sqrt{\pi n}}. \]

Para \(n\) de buen tamaño entonces \[ P(\text{partícula en el origen}) \approx \frac{1}{\pi n}. \]

Necesitamos sumar sobre los valores de \(n\). Recordemos del Problema 14 que \(\sum_{n=1}^{N} 1/n \approx \log N\) es un número que no tiene límite cuando \(N\) crece. Lo que hemos calculado es la probabilidad de que la partícula esté en el origen al final de los pasos numerados 2, 4, 6, 8, ..., \(2n\). Cada una de estas probabilidades es también el número promedio de veces que la partícula está en el origen al final de exactamente \(2n\) intentos. Para obtener el número promedio total de veces que la partícula está en el origen, sumamos porque la media de la suma es la suma de las medias. Por lo tanto, el número promedio de retornos al origen no tiene límite, y por lo tanto la probabilidad de retorno al origen es \(P = 1\). Y así cada partícula no solo regresa, sino que regresa infinitamente a menudo. Más cuidadosamente, debería decir que casi cada partícula regresa infinitamente a menudo, porque hay caminos tales como el curso constante hacia el noreste que permiten que algunas partículas se desvíen hacia el infinito. Pero la fracción de tales partículas entre todas ellas es cero.