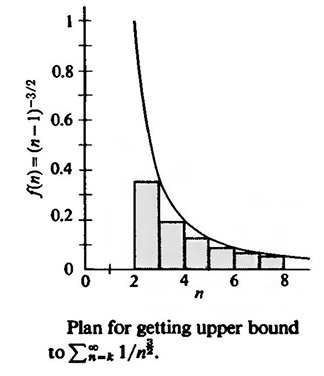
52. Paseo Aleatorio Tridimensional

Como en el paseo bidimensional, una partícula comienza en un origen O en tres dimensiones. Piense en el origen como centrado en un cubo de 2 unidades de lado. Un movimiento en este paseo envía la partícula con igual probabilidad a una de las ocho esquinas del cubo. Así, en cada movimiento la partícula tiene una probabilidad del 50-50 de moverse una unidad hacia arriba o hacia abajo, una unidad hacia el este o hacia el oeste, y una unidad hacia el norte o hacia el sur. Si el paseo continúa para siempre, encuentre la fracción de partículas que regresan al origen.

Solución para el Paseo Aleatorio Tridimensional

Ahora que sabemos que en una y dos dimensiones la partícula regresa al origen con probabilidad uno, ¿no es razonable pensar que seguramente regresará en cualquier número finito de dimensiones? Así lo creía, pero me equivoqué.

Tenemos tres coordenadas y la probabilidad de que las tres se anulen en el ensayo \(2n\) es

\[ P(\text{partícula en el origen}) = P(X = 0)P(Y = 0)P(Z = 0) = \left[ \binom{2n}{n} \left(\frac{1}{2}\right)^{2n} \right]^3 \]

Probemos nuevamente la aproximación de Stirling. Tenemos para tres dimensiones después de \(2n\) movimientos

\[ P(\text{partícula en el origen}) \approx \frac{1}{(\pi n)^{3/2}} \]

Podemos mostrar mediante métodos de integración que \(\sum \frac{1}{n^{3/2}}\) está acotada. Reemplace el número \(\frac{1}{n^{3/2}}\) por el área de un rectángulo cuya base va de \(n\) a \(n + 1\), y cuya altura es \(\frac{1}{n^{3/2}}\). Vea la figura. Trace una curva suave \(f(n) = \frac{1}{(n - 1)^{3/2}}\) a través de las esquinas superiores derechas de los rectángulos. El área bajo la curva excede el área del rectángulo:

\[ \int_{n}^{N} \frac{dx}{(x-1)^{3/2}} = \left[ \frac{-2}{(x-1)^{1/2}} \right]_{n}^{N} = \frac{2}{(n-1)^{1/2}} - \frac{2}{(N-1)^{1/2}} \]

Ahora, a medida que \(N\) tiende a infinito, el área tiende a \(\frac{2}{(n-1)^{1/2}}\), un número finito. Esto muestra que la media converge a un número finito.

Podemos evaluar ese número evaluando los primeros términos de la serie

\[ \sum_{n=1}^{\infty} \left[ \binom{2n}{n} \left(\frac{1}{2}\right)^{2n} \right]^3 \]

y luego aproximando el resto de la suma mediante métodos de integración. Obtengo 0.315. Después de, digamos, 10 o 20 términos, la aproximación de Stirling debería ser muy precisa, y el resto que necesita evaluación mediante integración es muy pequeño para entonces. Utilicé 18 términos. Este 0.315 es el número medio de retornos al origen por partícula. En consecuencia, \(1/Q = 1 + 0.315\), y obtenemos

\[ Q \approx 1/1.315 \approx 0.761. \]

Por lo tanto, la probabilidad \(P\) de que una partícula regrese al origen es aproximadamente 0.239.

Para aquellos que han visto los resultados del paseo aleatorio donde los pasos son hacia los centros de las caras del cubo circundante en lugar de hacia las esquinas, saben que la fracción que regresa es aproximadamente 0.35.* Aparentemente, entonces, 8 movimientos igualmente probables reducen la probabilidad de regresar más de 6.

Las mismas técnicas para un paseo aleatorio en 4 dimensiones, donde se lanzan 4 monedas para encontrar el vector que se añadirá a las coordenadas presentes, muestran que la probabilidad de retorno se reduce a 0.105.

Instrucciones para usar el código de la siguiente escena :

1. Escoge el número de pasos que se pueden dar en cada dirección (en realidad escoge ese número más uno).

2. Usa los botones "Un Paseo" y "100 Paseos" para realizar paseos y ver los resultados, el paseo termina con un regreso al origen o si llega a una cara del cubo grande azul.

3. Pulsa "Comenzar de Nuevo" para reiniciar la simulación.

4. Usa el ratón o los controles táctiles para rotar, hacer zoom y desplazar la cámara para ver el cubo desde diferentes ángulos.

Créditos
Traducción del problema 52 del libro Fifty challenging problems in probability , MOSTELLER

Vídeo introducción con lumen5.com