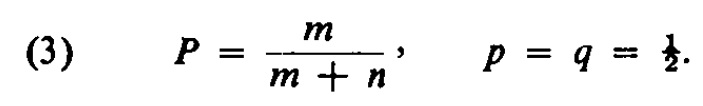El jugador M tiene $ 1, y el jugador N tiene $ 2 . Cada jugada le da a uno de los jugadores $ 1 del otro . El jugador M es lo suficientemente mejor que el jugador N como para que gane 2/3 de las jugadas . Juegan hasta que uno queda en bancarrota. ¿Cuál es la probabilidad de que el jugador M gane?

Solución

Nuestro problema es un caso especial del problema general de caminata aleatoria o suspense en el acantilado con dos barreras absorbentes . Históricamente, el problema surgió como un problema de apuestas, llamado "ruina del jugador", y muchos matemáticos famosos han contribuido a las preguntas que surgen de él .

Reformulemos el problema de manera general .

El jugador M tiene m unidades; el jugador N tiene n unidades . En cada jugada de un juego, un jugador gana y el otro pierde 1 unidad . En cada jugada, la probabilidad de que el jugador M gane es p, y la de que N gane es q = 1 - p . El juego continúa hasta que un jugador queda en bancarrota . La figura representa la cantidad de dinero del jugador M tiene en cualquier momento.

 Él comienza en x = m. Cuando x = 0, está en bancarrota; cuando x = m + n, el Jugador N está en bancarrota.

Con esta representación, dado que p > ½, podemos recurrir a un resultado de The Cliff - Hanger, Problema 35.

Sabemos que, si el Jugador M jugara contra un banco con recursos ilimitados, se habría declarado en bancarrota con probabilidad (q/p)^m.

En el transcurso de un viaje a la bancarrota, o bien alcanza una cantidad de dinero m + n (n es ahora finito), o nunca está tan bien.

Sea Q la probabilidad de que pierda contra el Jugador N  (lo que equivale a que el banco infinito gane sin que el Jugador M alcance nunca m + n). Entonces

( 1 )              ( q / p ) ^m = Q + ( 1 − Q ) ( q / p ) ^{m + n} ,

porque Q es la fracción de las secuencias que se absorben antes de llegar a m + n , y de la fracción 1 - Q que sí llegan a m + n ,

la porción ( q / p ) ^m+n también se absorbe en 0 si el juego se permite continuar indefinidamente .

Entonces P = 1 - Q es la probabilidad de que el Jugador M gane .

Haciendo sustituciones en la ecuación . ( 1 ) y resolviendo para P se obtiene