|
RULETA Doblar la apuesta
Hay una manera sencilla y absolutamente segura de ganar a la ruleta, siempre y cuando tengamos suficientes reservas. Una tirada de ruleta es igual que el lanzamiento de una moneda. Cada tirada es independiente, con una probabilidad del 50 por ciento de que la bola caiga en negro o rojo. En contra de lo que dice la intuición, tras una secuencia de veinte números negros consecutivos la probabilidad de que salga negro es exactamente la misma que la de que salga rojo (que podría parecer más probable). Esta falsa creencia, la de que es más probable que salga rojo, se conoce como la falacia del jugador. Así, pues, apostamos siempre al mismo color. Si perdemos, doblamos la apuesta en la siguiente tirada. Como el color elegido acabará saliendo en algún momento, el método producirá siempre un beneficio. Lo malo es que se necesita un buen fondo de reserva para continuar jugando. Una secuencia perdedora hace crecer las apuestas muy deprisa Hagamos los cálculos Si la apuesta en la primera jugada es de 1 euro, y no acierto hasta la décima, la tabla nos muestra lo que perdemos en cada jugada
La tercera columna muestra el dinero que he perdido hasta el momento. Cuando comienza la 10ª jugada he perdido 511, entregué 512 para la apuesta, en total 1023 y como me entregan 1024, las ganancias totales ascienden a la cantidad de 1 euro. Es probable que la rueda de la ruleta se lleve nuestro dinero durante más tiempo del que somos capaces de permanecer solventes. La pregunta es la siguiente, Si yo dispongo de 1023 euros para jugar al doble o nada, ¿me interesa (hablando en térmimos probabilísticos ) empezar la primera apuesta con más dinero de un euro? ¿Con cuanto dinero? Pongamos una regla: En cuanto gano paro, no antes. Si apuesto 1023 p(G) = 0.5. Dinero ganado 1023. No podría apostar en la segunda jugada, salvo que primera apuesta <= 1023/3= 341 Si apuesto 341, puedo ganar a la primera, o gano a la segunda , pues si los pierdo aún me queda lo justo para doblar la apuesta p(G)=B(2, 0.5)>0=0,75=3/4 Para poder alcanzar la tercera jugada, la primera tiene que ser menor o igual que 1023/7 (7=1+2+4) Si apuesto 1023/7~146, puedo ganar 146 pero puedo perder 1022 p(G)=B(3, 0.5)>0=0,875=7/8 Para poder alcanzar la cuarta jugada, la primera tiene que ser menor o igual que 1023/15 (15=1+2+4+8) Si apuesto 1023/15~68, si gano, 68; si no,pierdo 1020 p(G)=B(4, 0.5)>0=0,9375=15/16 Para poder alcanzar la 5ª apuesta, la primera tiene que ser menor o igual que 1023/31 (31=2^5-1) Si apuesto 1023/31~33, p(G)=B(5, 0.5)>0=0,96875=31/32
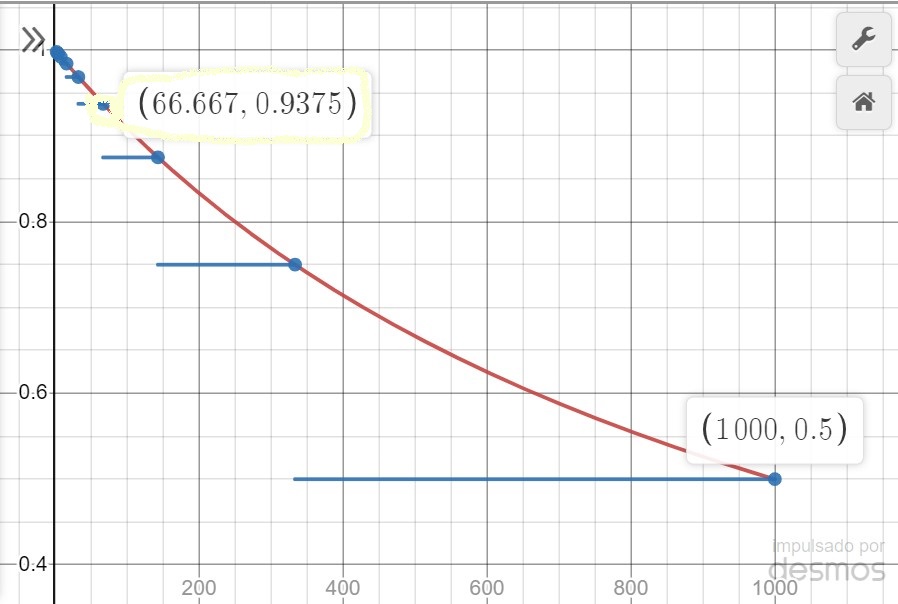
Al hacer clic en los puntos se ven las coordenadas, podemos variar C La magia de las matemáticas, sea C la cantidad que estamos dispuestos a perder (1023 en el ejemplo), la probabilidad de ganar en estos puntos x = C/(2^n-1) es (2^n-1)/2^n = C/(C+x) La magia es que esta cifra no tiene ni logaritmos ni potencias, es fácil verlo con una simple cuenta.
PROBLEMA 1 Estoy dispuesto a perder al doble o nada hasta 1000 euros si es con una probabilidad menor del 10 % ¿Que dinero debo poner en la primera apuesta? 10%=0.10, es 1-p(G), su log en base 2 es, -3.32192809489 tomamos el entero inferior -4 y como primera apuesta 1000/(2^4-1)~66 así la probabilidad de perder será menor del 10% y si gano, ganaré 66 euros. Sin hacer la cuenta podíamos haber buscado el valor en la gráfica, con C=1000 y buscando la mayor x cuya probabilidad es mayor que 90% , 66,6667
=============
Ahora nos encaminamos a proponer un nuevo problema que surge aquí.
Con una apuesta inicial de 66 euros , si tengo un capital
disponible para jugar de 1000 euros , la probabilidad de ganar
es del 93,75% . Si juego muchas partidas ganaré 66 euros en el
93,75% de las veces pero perderé 990 euros las otras. Calculemos
las ganancias aproximadas en 10000 partidas 9375 · 66 - 990 · 625 = 0 Evidente pero curioso Si hacemos una partida hasta llegar a lo que perdemos TENDREMOS LA PROBABILIDAD p(G) para esa apuesta.
PROBLEMA 2 Vamos a calcular sin tablas de binomial y sin calculadora la probabilidad de ganar si apuesto 200 euros y dispongo de un capital de 1000 euros Solución Calculo la pérdida 1ª ap 200 me quedan 800 pierdo 2ª ap 400 me quedan 400 pierdo Ya no me queda dinero para la 3ª apuesta , me voy con 400 euros, perdí 600 euros p · 200 + (p - 1) · 600 = 0 800p = 600 p = 0.75
Prueba a jugar 66 euros al doble o nada con la escena de descartes.
Dejamos una captura del resultado obtenido con la escena después de diez mil partidas, la p(G) muy cerca de lo calculado con las cuentas o con la gráfica. La ley de los grandes números no falla.
¿Quién dijo que este era un juego seguro? Después de diez mil partidas me voy habiendo perdido 5280 € Mientras las partidas hemos observado que cuando p(G) era menor de lo esperado, 93,75%, el total ganado sale negativo, Y ya que hemos capturado el vídeo de estas 10000 partidas, lo compartimos aquí
Consolación Ruiz Gil Febrero 2024 https://www.matsolin.com/ruleta/index.htm
|