La Matemática del SudokuTom Davis http://www.geometer.org/mathcircles (Preliminar) 13 de septiembre de 2012 1 IntroducciónEl Sudoku es un rompecabezas presentado en una cuadrícula que generalmente es de 9 × 9, pero a veces es de 16 × 16 u otros tamaños. En este documento, solo consideraremos el caso de 9 × 9, aunque casi todo lo que se dice se puede extender fácilmente a rompecabezas con diferentes dimensiones. Los rompecabezas de Sudoku se pueden encontrar en muchos periódicos diarios, y hay miles de referencias a ellos en internet.
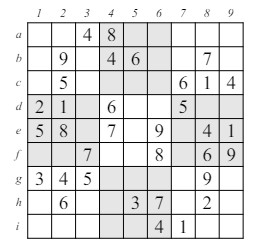
Figura 1: Un rompecabezas de sudoku fácil La cuadrícula original tiene algunos de los cuadrados llenos con los dígitos del 1 al 9 y el objetivo es completar la cuadrícula para que cada fila, columna y subcuadrícula de 3 × 3 (de las cuales hay 9) contenga cada uno de los dígitos exactamente una vez. Algunas configuraciones iniciales admiten cero soluciones y otras admiten múltiples soluciones, pero estas generalmente se consideran rompecabezas inválidos. En la figura 1, un rompecabezas (relativamente fácil) aparece a la izquierda. Si nunca has intentado resolver un rompecabezas de sudoku, sería muy informativo intentar resolver este ahora, y ver qué estrategias puedes idear antes de leer el resto de este artículo. Probablemente tomará más tiempo de lo que piensas, ¡y obtendrás mucho! mejorarás mucho con la práctica. Y si eres un principiante, incluso si estás acostumbrado a resolver el crucigrama dominical del New York Times con bolígrafo, usa un lápiz la primera vez que intentes resolver un sudoku! El Sudoku es interesante tanto como un ejercicio lógico (¿Cuáles son las buenas estrategias para encontrar una solución?) como un objeto matemático (¿Cuántas cuadrículas de sudoku hay? ¿Cuántas son esencialmente diferentes? ¿Cuál es la matemática subyacente y la lógica detrás de algunas técnicas de solución?). Todos estos aspectos se explorarán aquí. Primero discutiremos varias técnicas de solución y cualquier matemática relacionada se discutirá junto con la técnica. Al final, incluiremos alguna información que es mayormente matemática y probablemente no será de mucha ayuda para encontrar soluciones de sudoku. En lo que sigue, usaremos la siguiente terminología. Hay una gran literatura sobre sudoku en internet y, en la medida de lo posible, intentaremos usar la misma terminología en este artículo que la comúnmente usada en internet.
2 Estrategias ObviasComenzaremos con algunas estrategias que son en cierto sentido totalmente obvias, aunque buscarlas en un rompecabezas a veces puede ser difícil, ya que hay muchas cosas que buscar. La mayoría de los rompecabezas tienen una calificación de dificultad, y casi todos los rompecabezas fáciles y muchos rompecabezas intermedios se pueden resolver completamente usando solo las técnicas mencionadas en esta sección. Comenzaremos con las observaciones más obvias y procederemos a algunas que son un poco más interesantes. Los métodos se presentan aproximadamente en orden de dificultad creciente para un ser humano. Para una computadora, se pueden usar enfoques completamente diferentes y a menudo son más simples.
2.1 Candidato Único FaltanteSi ocho de los nueve elementos en cualquier fila, columna o bloque (o "línea virtual") ya están determinados, el elemento final tiene que ser el que falta. Esta técnica se utiliza mucho hacia el final de una solución cuando la mayoría de los cuadros ya están llenos. Una declaración similar obvia es esta: si ocho de los nueve valores son imposibles en un cuadro dado, el valor de ese cuadro debe ser el noveno.
2.2 candidatos únicos
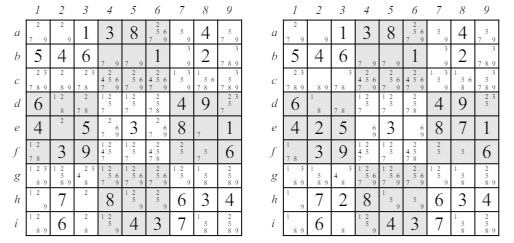
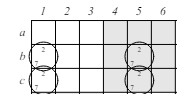
Figura 2: Eliminación de Candidatos y candidatos únicos
Para cualquier posición de sudoku dada, imagina listar todos los candidatos del 1 al 9 en cada cuadro sin llenar. Luego, para cada cuadro cuyo valor v se determina, tacha cada instancia de v como un candidato posible en la fila, columna y bloque (o, en las tres líneas virtuales) a las que pertenece ese cuadro. Los valores restantes en cada cuadro representan valores posibles que podrían insertarse allí. Si, después de tal eliminación de los candidatos imposibles, solo queda un valor posible, esa situación se refiere como un "único candidato" y ese valor restante se puede asignar al cuadro. En el ejemplo del lado izquierdo de la figura 2 vemos un rompecabezas de sudoku donde los números más grandes en los cuadros representan valores que ya están llenos. Los cuadros cuyos valores aún no están determinados se llenan con una lista de candidatos posibles, donde los valores en los cuadros completados se han usado para eliminar algunos valores. Después de que estas eliminaciones obvias de candidatos han ocurrido, podemos ver que el rompecabezas contiene tres candidatos únicos en e2 y h3 (donde debe insertarse un 2), y en e8 (donde debe insertarse un 7). Nota que una vez que has llenado estos valores, aparecerán otros candidatos únicos. Por ejemplo, tan pronto como el 2 está insertado en h3, puedes eliminar los 2 como candidatos en su fila, columna y bloque, y cuando esto está hecho, i3 se convertirá en un único candidato que debe llenarse con 8. La posición en el lado derecho de la figura 2 muestra el resultado del rompecabezas anterior después de que los tres cuadros mencionados en el párrafo anterior han sido llenados y los candidatos obvios han sido eliminados de los cuadros no llenos.
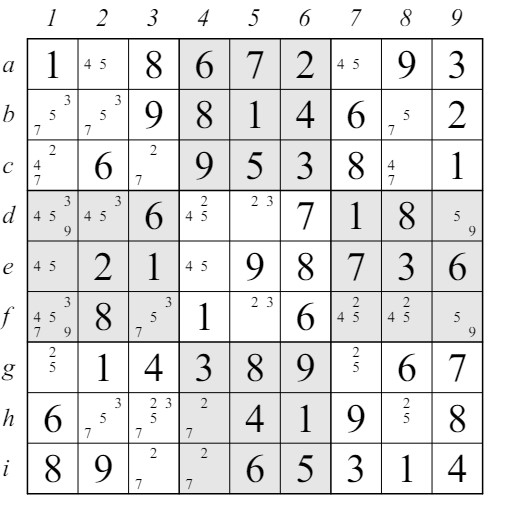
2.3 Únicos OcultosA veces hay celdas que, de hecho, tienen solo un valor posible basado en la situación, pero una simple eliminación de candidatos en la fila, columna y bloque de esa celda no lo hace obvio. Si vuelves a examinar la situación en el lado izquierdo de la figura 2, hay un único oculto en la casilla g2 cuyo valor debe ser 5. Los dos 5 en b1 y e3 requieren que el 5 que debe aparecer en el bloque inferior izquierdo (ghi123) debe ocurrir en la columna 2. Pero solo hay una casilla disponible en la columna 2 de ese bloque que no está llena. Así que 5 puede ser colocado en la casilla g2. El 5 en la casilla g2 está "oculto" en el sentido de que sin un examen más profundo, parece que los valores 1, 2, 5, 8 y 9 son todos candidatos posibles. Una manera fácil de encontrar únicos ocultos es buscar en cada línea virtual un candidato que aparece en solo una de las casillas. Si eso ocurre, has encontrado un único oculto. El ejemplo anterior es para un único oculto en un bloque. Lo mismo puede ocurrir en cualquier línea virtual. Usando el mismo ejemplo en la figura 2, hay un único oculto en la casilla d9 donde debe colocarse un 3. Un 3 debe aparecer en algún lugar en la fila d, pero los 3 en los dos bloques más a la izquierda que contienen la fila d ya contienen un 3 por lo que el 3 debe ir en d7, d8 o d9. Dado que las casillas d7 y d8 ya están llenas, d9 contiene un único oculto. La aplicación de cualquiera de las técnicas en esta sección asigna inmediatamente un valor a una casilla. La mayoría de los rompecabezas que se clasifican como "fáciles" y muchos que se clasifican como "intermedios" se pueden resolver completamente utilizando solo estos métodos. El resto de los métodos que consideraremos no te permiten llenar automáticamente una casilla. Lo que hacen es eliminar ciertos candidatos de ciertas casillas. Obviamente, una vez que todos los candidatos menos uno han sido eliminados, entonces el valor que se debe colocar en esa casilla está completamente determinado.
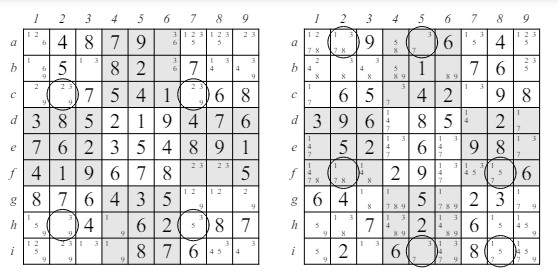
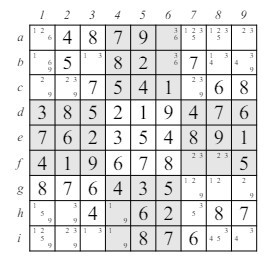
3 Candidatos BloqueadosA veces puedes encontrar un bloque donde las únicas posiciones posibles para un candidato están en una fila (o columna) dentro de ese bloque. Dado que el bloque debe contener el candidato, el candidato debe aparecer en esa fila (o columna). Pero eso significa que puedes eliminar al candidato como una posibilidad en la intersección de esa fila (o columna) con otros bloques. Una situación similar puede ocurrir cuando un número que debe ir en una fila o columna solo puede ocurrir dentro de uno de los bloques que intersectan esa fila o columna. Por lo tanto, el candidato debe estar en la intersección de la fila/columna y el bloque y, por lo tanto, no puede ser un candidato en ninguna de las otras casillas que conforman el bloque. Todas estas situaciones están ilustradas en la figura 3. El bloque def789 debe contener un 2, y los únicos lugares donde esto puede ocurrir están en las casillas f7 y f8: ambas en la fila f. Por lo tanto, 2 no puede ser un candidato en ninguna otra casilla de la fila f, incluyendo la casilla f5 (por lo que f5 debe contener un 3). De manera similar, el 2 en el bloque ghi456 debe estar en la columna 4, por lo que 2 no puede ser un candidato en ninguna otra casilla de esa columna, incluyendo d4. Finalmente, el 5 que debe ocurrir en la columna 9 tiene que caer dentro del bloque def789, por lo que 5 no puede ser un candidato en ninguna de las otras casillas d7, incluyendo f7 y f8.
Figura 3: Candidatos Bloqueados
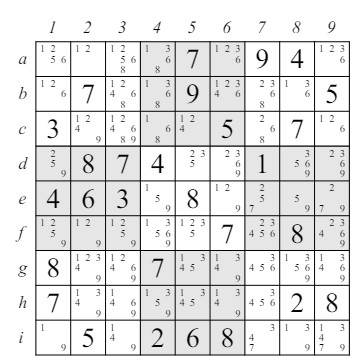
4 Pares, Tríos y Cuartetos únicos y Ocultos, etc.Estos son similares a los candidatos únicos, discutidos en la sección 2.2, excepto que en lugar de tener solo un candidato en una celda, tienes los mismos dos candidatos en dos celdas (o, en el caso de tríos únicos, los mismos tres candidatos en tres celdas, etcétera). El par, trío o cuarteto único puede estar en la misma línea virtual, y cuando ocurre, esos valores deben usar todas las casillas. Así, esos candidatos se eliminan de cualquier otra casilla en esa línea virtual. La figura 4 muestra cómo se puede usar un par único. En las casillas a2 y a8, los únicos candidatos que aparecen son 2 y 7. Eso significa que esas casillas deben llenarse con esos números, en algún orden. Pero eso significa que el 2 y el 7 no pueden estar en ninguna de las otras casillas en esa fila, por lo que 2 se puede eliminar como candidato en a3 y tanto 2 como 7 se pueden eliminar como candidatos en a9.
Figura 4: Un Par Único En el caso de pares únicos, ambas casillas deben tener exactamente los mismos dos candidatos, pero en el caso de tríos únicos, cuartetos, etcétera, el único requisito es que los tres valores sean los únicos valores que aparecen en esas casillas en alguna línea virtual. Por ejemplo, si tres entradas en una fila tienen los siguientes conjuntos de candidatos: {1, 3}, {3, 7} y {1, 7} entonces es imposible que un 1, un 3 o un 7 aparezcan en cualquier otra casilla de esa fila. La idea es bastante simple y se ilustra en la figura 5. En la fila a, las casillas a2, a8 y a9 contienen el trío único que consiste en los números 1, 3 y 7. Así, esos números deben aparecer en esas casillas en algún orden.
Figura 5: Un Trío Único Por esa razón, los candidatos 1 y 3 pueden ser eliminados de las casillas a4 y a5.
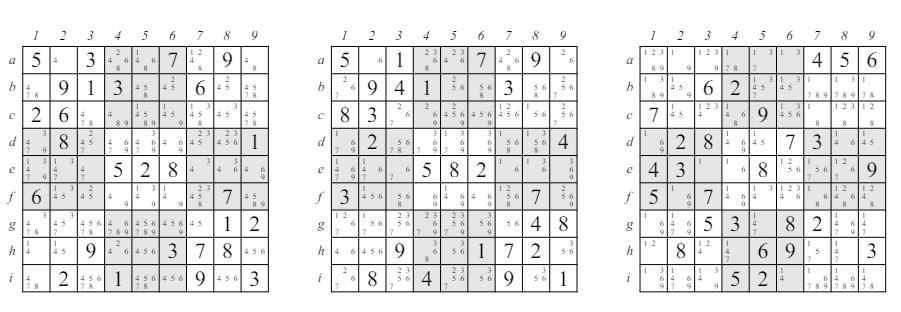
Figura 6: Un Trío Oculto Los pares, tríos y cuartetos ocultos están relacionados con los pares, tríos y cuartetos únicos de la misma manera que los únicos ocultos están relacionados con los únicos únicos. En la figura 6 considera la fila i. Las únicas casillas en la fila i en las que aparecen los valores 1, 4 y 8 son i1, i5 e i6. Por lo tanto, podemos eliminar los candidatos 2 y 6 de la casilla i1 y el candidato 3 de i5. Recuerda, por supuesto, que estos conjuntos ocultos pueden aparecer en cualquier línea virtual: una fila, columna o bloque. Tampoco hay razón para que no pueda haber un quinteto, sexteto único u oculto, etc., especialmente para las versiones de sudoku que son más grandes que 9 × 9.
5 Configuraciones de X-Wings y SwordfishUna configuración de x-wing ocurre cuando el mismo candidato ocurre exactamente dos veces en dos filas y en las mismas columnas de esas dos filas. (O de manera similar, si intercambias las palabras "fila" y "columna" en la oración anterior.) En la configuración de la izquierda en la figura 7, el candidato 3 ocurre dos veces en las filas c y h y en esas dos filas, aparece en las columnas 2 y 7. No importa que el candidato 3 aparezca en otros lugares del rompecabezas. Las casillas donde el candidato x-wing (3, en este caso) puede formar un rectángulo, por lo que un par de esquinas opuestas de ese rectángulo deben contenerlo. En el ejemplo, esto significa que los 3 están en c2 y h7 o están en c7 y h2. Tal vez el hecho de que conectar los pares posibles formaría una 'X', como los cazas X-wing en Star Wars, da nombre a esta estrategia. En cualquier caso, dado que las dos esquinas pueden contener al candidato, ninguna otra casilla en las columnas o filas que contienen las esquinas del rectángulo puede contener a ese candidato. En el ejemplo, podemos concluir que 3 no puede ser un candidato en las casillas a7, f7 o i2. Un swordfish es similar a un x-wing, excepto que debe haber tres filas/columnas con los tres candidatos apareciendo en al menos tres columnas/filas. Al igual que con los pares y tríos únicos y ocultos, para un swordfish no hay requisito de que el candidato esté en las tres posiciones. La razón es similar a la utilizada para el x-wing; sin embargo, una vez que encuentras una configuración de swordfish, el candidato no puede aparecer en ninguna otra casilla de las tres columnas y filas. Una configuración de swordfish aparece en la figura 7 a la derecha. En este caso, el candidato es 7, y las columnas que forman el swordfish son 2, 5 y 8. El valor 7 aparece solo en las filas a, f y i. Uno debe aparecer en
Figura 7: X-Wing (izquierda) y Swordfish
en cada una de estas filas y en cada una de las columnas, por lo que ninguna otra casilla en esas filas y columnas puede contener un 7. Así, el candidato 7 puede eliminarse de a1, f1, f6, i6 e i9. Por supuesto, no hay nada especial acerca de una configuración de 3×3; "super-swordfish" con 4, 5 o 6 candidatos podría ser posible, pero son raros y no particularmente difíciles de detectar. El "super-swordfish" con 4 filas y 4 columnas a veces se llama "medusa". Si estás jugando en una cuadrícula estándar de 9×9, la situación más compleja que necesitarías buscar sería una medusa, ya que si hubiera un super-swordfish de 5×5, también tendría que haber un swordfish de 4×4 o más pequeño en las filas o columnas restantes. Es una lástima que no haya una verdadera necesidad para el super-swordfish de 5×5, ya que en la "literatura" web, se le llama "squirmbag".
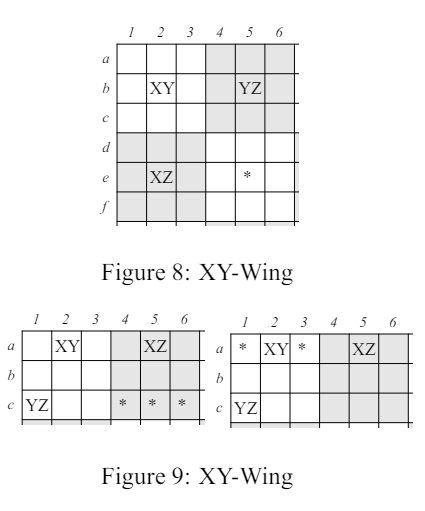
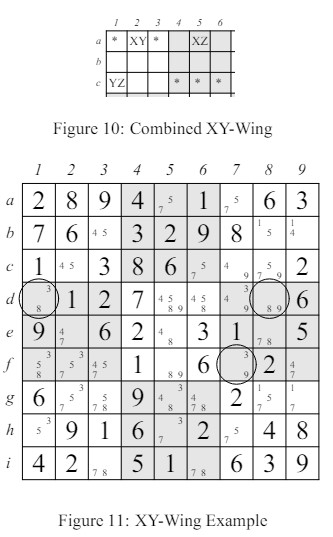
6 El XY-WingLa idea básica del xy-wing es esta: A veces una casilla tiene dos candidatos. Si asumimos que el primero se usa, entonces eso fuerza una cierta conclusión. Si, al asumir que el segundo es verdadero, se llega a la misma conclusión, entonces esa conclusión debe ser verdadera sin importar cómo se haga la elección inicial, la conclusión debe seguir. En la configuración en la figura 8, supongamos que hay dos candidatos posibles en las casillas b2, b5 y e2, como se muestra. Considera el contenido de la casilla b2. Si X está allí, entonces debe haber un Z en e2 y por lo tanto Z no puede ser un candidato en e5. Pero la otra posibilidad es que b2 sea Y. En este caso, b5 debe ser Z y, de nuevo, e5 no puede ser Z. Así, en una configuración como esta, puedes eliminar Z como candidato en la casilla e5. De manera similar, considera la configuración a la izquierda en la figura 9. Si Y o X es verdadero, las tres casillas indicadas por asteriscos no pueden tener Z como candidato. De manera similar, examinando la configuración a la derecha en la misma figura, Z se elimina como candidato en dos casillas más indicadas por asteriscos.
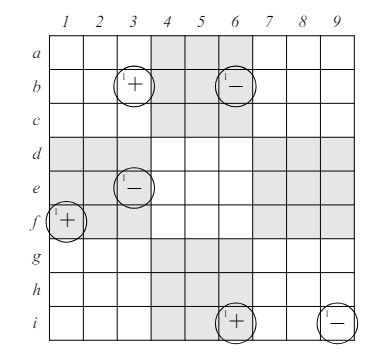
Obviamente, las dos configuraciones en la figura 9 se pueden combinar para formar la figura 10 donde Z puede ser eliminado como candidato en cualquiera de las casillas marcadas con un asterisco. Un ejemplo de un xy-wing en un rompecabezas real aparece en la figura 11. Observa que en las casillas d8 y f7 (ambas en el mismo bloque, def789) y en la casilla d1 tenemos candidatos {8, 9}, {3, 9} y {8, 3}, respectivamente. Debido a esto, podemos eliminar 3 como candidato en las casillas d7, f1 y f2.
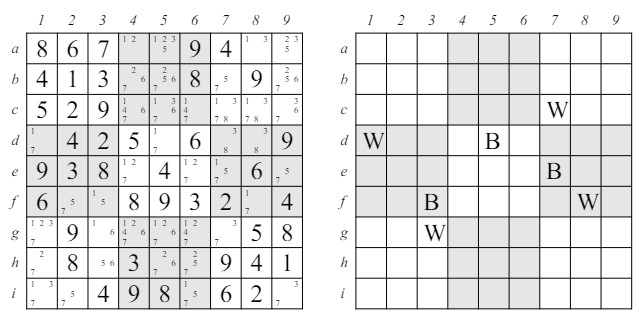
7 Coloreado y MulticoloreadoEl coloreado y multicoloreado son técnicas que infieren colores basados en cadenas lógicas de deducción. El método de coloreado, especialmente, es lo suficientemente simple como para que se pueda hacer a mano. 7.1 Coloreado SimpleConsidera el ejemplo en la figura 12 donde consideramos unas pocas casillas que contienen el candidato 1. Supongamos por ahora que estos son los únicos lugares posibles para el 1 en el rompecabezas. Ciertas líneas virtuales contienen exactamente dos lugares donde el candidato 1 puede ir: fila b, fila i, columna 3 y bloque de3f123. En cada una de estas líneas virtuales, solo una de las casillas posibles puede contener un 1 y una vez que se selecciona, la otra no puede. Pero esto crea una especie de "cadena" si f1 contiene 1, entonces e3 no debe, y como e3 no debe, b3 debe, por lo que b6 no debe, i6 debe, y i9 no debe. Si, por otro lado, f1 no contiene un 1, entonces la misma serie de interacciones de línea virtual forzarán una alternancia de conclusiones y cada cuadrado en la cadena tendrá que tener el valor opuesto. En la figura hemos marcado las casillas con + y – según la suposición de que f1 contiene un 1, pero por supuesto puede ser el caso de que f1 no contenga un 1, y todos los + y – signos se intercambiarían. Más que usar los caracteres + y –, que implican la presencia o ausencia de un valor, es más simple imaginar colorear cada casilla en la cadena de blanco o negro, y
Figura 10: XY-Wing Combinado ya sea que todas las casillas negras tengan un 1 y todas las casillas blancas no, o viceversa. Supongamos ahora que para algún candidato has descubierto tal "cadena" y la has coloreado de esta manera alterna. Puede ser que haya casillas adicionales donde el candidato podría posiblemente ocurrir que no estén en la cadena de color. En el ejemplo anterior, supongamos que la casilla f1 está coloreada de negro y así la casilla i9 debe estar coloreada de blanco. Considera la casilla f9 que se encuentra en la intersección de la fila de f1 y la columna de i9. Ya que f1 y i9 tienen colores opuestos, exactamente uno de ellos contendrá un 1, y por lo tanto es imposible que la casilla f9 contenga un 1, por lo que puede ser eliminada como candidato en esa casilla. No hay nada especial acerca de una intersección fila-columna. Cada vez que dos casillas de colores opuestos se "intersectan" vía líneas virtuales o cualquier clase de soporte en otra casilla, el candidato puede ser eliminado como una posibilidad en esa casilla. Esto es probablemente más fácil de ver con el ejemplo concreto mostrado en la izquierda en la figura 13 donde consideramos las interacciones entre casillas con 1 como un posible candidato. En la fila d, d1 y d5 son las únicas ocurrencias del candidato 1, así que coloreamos d5 negro y d1 blanco. Pero d1 y f3 son las únicas posibilidades para el 1 en el bloque de3f123, así que ya que d1 es blanco, f3 es negro. De manera similar, ya que f3 es negro, g3 y
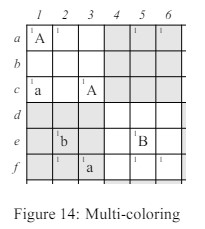
Figura 12: Coloreado Simple f8 son blancas. Dado que f8 es blanca, e7 es negra, y dado que e7 es negra, c7 es blanca. Es una cadena bastante complicada, pero aquí está lo que tenemos: negro: {d5, f3, e7} blanco: {d1, g3, f8, c7}. Una cuadrícula que muestra solo las casillas coloreadas aparece a la derecha en la figura 13. La casilla c5 está en la intersección de la fila de c7 y la columna de d5, pero c7 es blanca y d5 es negra, por lo que 1 no puede ser un candidato en la casilla c5. De manera similar, la casilla g5 está en la misma fila que g3 y la misma columna que d5, que son blancas y negras, respectivamente, por lo que 1 tampoco puede ser un candidato en g5. 7.2 MulticoloreadoA veces una posición puede ser coloreada para un candidato particular y existen múltiples cadenas de coloreado, pero ninguna de ellas se puede usar para eliminar ese candidato de otras casillas. Si hay múltiples cadenas, vale la pena buscar una situación de multicoloreado. Considera el rompecabezas en la figura 14. Supón que en las partes del rompecabezas que no se muestran no hay otros lugares donde pueda ir el candidato 1. Cuando este diagrama está coloreado, hay dos cadenas de coloreado. En lugar de usar palabras como "negro" y "blanco", usaremos letras, como A, B, a y b donde A y a representan casillas opuestas, al igual que B y b, y así sucesivamente. En la figura 14, las filas a y c y en la columna 3 hay solo dos posiciones posibles para el candidato 1. Cuando esta cuadrícula está coloreada, se verá algo así: las casillas c1 y f3 tienen el color A y la casilla c3 tiene el color B. La casilla a2 tiene el color b y la casilla a5 tiene el color B. (Nota que los colores asignados son arbitrarios. Todo lo que importa es que las casillas c1 y f3 tienen el mismo color que es el opuesto de c3 y que a2 y a5 tienen colores opuestos que son diferentes de los otros colores asignados. Nota que ninguna de las otras casillas con 1 como candidato puede ser coloreada, ya que todas están en líneas virtuales con más de dos casillas que potencialmente pueden contener un 1. Si consideramos la casilla "a" como equivalente a la oración: "Cada casilla que contiene el color a contiene un 1 y
Figura 13: Coloreado Simple Figura 14: Multicoloreado 1," y así sucesivamente, entonces podemos escribir pequeñas expresiones lógicas que indican las relaciones entre los varios colores cuando son interpretados como oraciones. Las obvias son de la forma: "a = ¬A" o "A = ¬a" (donde el símbolo lógico "¬" significa "no"). En otras palabras, si a es verdadero, entonces A no lo es, y viceversa. Aunque los valores de colores no opuestos no necesariamente tienen algo que ver entre sí, en la figura 14, el par a y b, por ejemplo, están vinculados, ya que ocurren en el mismo bloque. Si a es verdadero, entonces b no puede ser, y viceversa, pero puede ser verdadero que tanto a como b sean falsos. Expresaremos esta relación como "a!b" y lo leeremos como "a excluye b". Obviamente, si a!b entonces b!a. Además, es obvio en la configuración de la figura 14 que b!A. Otra forma de pensar en a!b es como "Si a es verdadero entonces b es falso". De manera similar, significa "Si b es verdadero entonces a es falso". Si a!b entonces al menos uno de a o b debe ser falso. Eso significa que al menos uno de A o B debe ser verdadero. Eso significa que cualquier casilla en la intersección generalizada de casillas coloreadas A y B no debe permitir el candidato ya que una de las dos casillas coloreadas A o B debe contener el candidato. En la figura 14, esto significa que 1 no puede ser un candidato en la casilla f5. Para condensar todo lo anterior en una sola declaración, sabemos que si a!b para algún candidato, entonces cualquier casilla en la intersección generalizada de A y B no puede contener ese candidato.
Figura 15: Ejemplo de Multicoloreado: Coloreado a la Derecha Pero se puede hacer mucho más. En situaciones complejas, puede haber muchas cadenas de colores independientes con los colores A y a, B y b, C y c, y así sucesivamente. Cuando eso ocurre, necesitamos buscar las consecuencias de la siguiente inferencia: Si a!b y B!c entonces a!c. No es difícil ver por qué: Si a es verdadero, b no lo es, entonces B es verdadero, y la segunda exclusión implica que c no lo es. El razonamiento se invierte trivialmente para mostrar que si c es verdadero entonces a no lo es, así que obtenemos a!c. Así que para hacer multicoloreado para un candidato particular, procede de la siguiente manera:
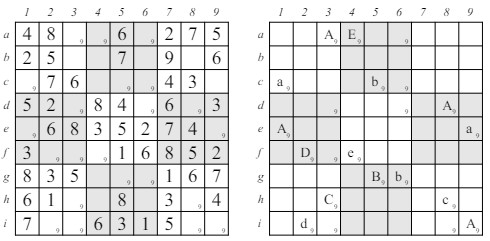
Veamos una aplicación de multicoloreado muy compleja. Ve la figura 15 donde solo se marcan las casillas que admiten al candidato 9 (por supuesto, todavía podrían admitir otros candidatos). A la izquierda está la cuadrícula completa y a la derecha hay una versión simplificada donde solo se muestran las casillas que admiten al candidato 9 en un mostradas, y todas las cadenas de colores están representadas. Es un excelente ejercicio mirar el diagrama a la derecha para asegurarse de entender exactamente cómo están construidas las cadenas de colores. El siguiente paso en la aplicación del multicoloreado es encontrar todos los pares de exclusión, y la lista inicial es la siguiente. Nota que la operación "!" es conmutativa, por lo que si piensas que a!b debería estar en la lista y no lo está, asegúrate de buscar también b!a.
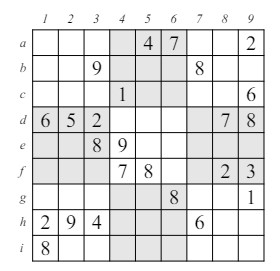
A!E a!b D!e A!d A!C A partir de estas exclusiones iniciales, se pueden deducir otras. Por ejemplo, de a!b y A!d podemos concluir que b!d. Nota que para hacer esta implicación, estamos utilizando implícitamente el hecho de que a!b y b!a son equivalentes. De hecho, si hacemos todas esas deducciones, y luego todas las deducciones a partir de esas, y así sucesivamente, hay diez exclusiones adicionales que encontramos:
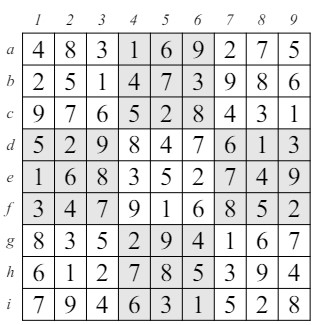
b!d b!C b!c b!D C!e Para la mayoría de ellas, necesitamos buscar intersecciones generalizadas de los opuestos de los valores de exclusión. Por ejemplo, dado que A!e y hay una A en c1 y una E en a4, entonces 9 no puede ser un candidato en c6. Además, dado que tenemos A!A y b!b, podemos concluir que a y B son verdaderos. Para facilitar la comprobación de las consecuencias de estas implicaciones de exclusión, la figura 16 muestra la solución completa del rompecabezas en la figura 15.
Figura 16: Solución al Ejemplo de Multicoloreado
8 Restricciones de Solución ÚnicaSi sabes que el rompecabezas tiene una solución única, lo cual cualquier rompecabezas razonable debería tener, a veces esa información puede eliminar algunos candidatos. Por ejemplo, examinemos el ejemplo en la figura 17. En la fila g, columnas 4 y 6, los únicos candidatos posibles son 1 y 2. Pero en la fila g, columnas 4 y 6, los candidatos son 1, 2 y 8. Decimos que 8 debe aparecer en g4 o g6. Si no lo hace, entonces las cuatro esquinas de
Figura 17: Restricción de Unicidad la casilla c4, c6, g4 y g6 tendrán exactamente los mismos dos candidatos, 1 y 2, por lo que podríamos asignar el valor 1 a cualquier par de esquinas opuestas, y ambas deben generar soluciones válidas. Si hay una solución única, esto no puede ocurrir, por lo que una de g4 o g6 debe contener el valor 8. Pero si ese es el caso, la casilla i4 no puede ser 8, así que el candidato 8 puede ser eliminado de la casilla i4. Además, dado que g4 o g6 deben ser 8, g8 no puede ser 8, ya que está en la misma fila que las otras dos. En la misma figura, una situación similar aparece en otro lugar. Ve si puedes encontrarla. Pista: está orientada a columnas en lugar de filas.
Figura 18: Un bloque ilegal Regresemos y veamos exactamente qué está ocurriendo, y a partir de eso, podremos encontrar una serie de técnicas basadas en la misma idea general. La figura 18 muestra un bloque ilegal básico. Cualquier cosa puede ocurrir en las casillas que no están rodeadas, pero nota que una asignación de un 2 o un 7 a cualquiera de las casillas rodeadas fuerza los valores de las otras en un patrón alternante. Pero cualquiera de las casillas puede ser asignada a un 2 o un 7 y el patrón resultante será legal, y esto significa que hay dos soluciones válidas para el rompecabezas. Esto significa que si alguna asignación causa que se forme un bloque ilegal, esa asignación es imposible, y podemos usar ese hecho para eliminar ciertas posibilidades, como lo hicimos en el ejemplo de la figura 17. Nota que las cuatro esquinas no solo forman un rectángulo, sino que deben ser arregladas para que dos pares de esquinas adyacentes estén dentro de los mismos bloques. Si las cuatro esquinas están en bloques diferentes, entonces las restricciones de esos bloques diferentes pueden forzar los valores de una manera u otra.
Figura 19: Consideraciones de Unicidad Ahora examinemos algunas variaciones de este tema. En el resto de los ejemplos en esta sección, asumiremos que las casillas vacías se pueden llenar con cualquier entrada válida del rompecabezas: vacías o determinadas. En la figura 19 de la izquierda, veamos algo que es casi lo mismo que vimos en la figura 18 y lo único que lo hace legal es la presencia de la posibilidad de un 3 en la casilla b1. Si no es un 3, entonces tendríamos el bloque ilegal, por lo que debe haber un 3 en la casilla b1. Nota que si, en la figura, la casilla b1 hubiera contenido las posibilidades 2, 3, 4 y 7, al menos las dos posibilidades 2 y 7 podrían ser eliminadas como posibilidades, así que solo un 3 o un 4 podría ser ingresado en esa casilla. El ejemplo en el medio de la figura 19 es similar al ejemplo original en esta sección, excepto que la ocurrencia de número adicional ocurre en dos bloques diferentes en lugar de uno. Como antes, al menos una de esas casillas debe contener el número (3 en este caso), así que el valor 3 se puede eliminar de cualquiera de las otras casillas en esa fila (fila b, en este caso), pero no en ninguno de los bloques, ya que la que se fuerza a ser 3 podría estar en el otro bloque. El ejemplo en la derecha en la figura 19 ilustra otro tipo de deducción que podría hacerse. Sabemos que al menos una de b1 y c1 debe contener un número diferente a un 2 o un 7, pero no sabemos cuál. Si pensamos en la combinación de las dos casillas como una unidad, sabemos que esta unidad contendrá un 3 o un 4. Esta unidad de dos casillas, junto con la casilla a3 (que tiene 3 y 4 como sus únicas posibilidades) significa que ninguna otra casilla en el bloque abc123 puede contener un 3 o un 4. Si la casilla 34 hubiera estado en a1, podríamos además eliminar 3 y 4 como candidatos de cualquiera de las otras casillas en la columna 1 fuera del primer bloque. Nota que podemos tener tanto un 3 como un 4 en cualquiera o ambas casillas b1 y c1 en este ejemplo en la derecha. Mientras ambos ocurran, el argumento se mantiene. También nota que si los 3 y 4 aparecen en la fila b y las entradas en la fila c fueran ambas 2, y la casilla 34 estuviera en la fila b, podríamos eliminar cualquier otro 3 o 4 en esa fila.
9 Cadenas ForzadasEste método es casi como adivinar, pero es una forma de adivinar que no es demasiado difícil para un humano. Hay varios tipos de cadenas forzadas, pero la más fácil de entender funciona solo con celdas que contienen dos candidatos. La idea es esta: para cada una de las celdas de dos candidatos, selecciona tentativamente el valor del primero y ve si eso fuerza cualquier otra celda de dos candidatos a tomar un valor. Si lo hace, encuentra celdas adicionales de dos candidatos cuyos valores también estén forzados y continúa hasta que no haya más celdas forzadas. Luego repite el operación asumiendo que la celda original tenía el otro valor. Si, después de hacer todos los movimientos forzados posibles con una suposición y con la otra, existe una celda que se ve obligada a tomar el mismo valor, no importa qué, entonces ese debe ser el valor para esa celda. Como ejemplo, considera el ejemplo en la figura 20, y comencemos con la celda b3 que puede contener un 1 o un 3. Si b3 = 1, entonces i3 = 3, así que h2 = 9, entonces h4 = 1. Por otro lado, si b3 = 3, entonces i3 = 1, así que i4 = 9, entonces h4 = 1. En otras palabras, no importa qué valor asumimos que toma b3; cualquiera de las dos suposiciones lleva a la conclusión de que h4 = 1, por lo que podemos asignar 1 a la celda h4.
Figura 20: Cadenas Forzadas 10 AdivinanzaLos métodos anteriores resolverán casi cualquier rompecabezas de sudoku que encuentres en los periódicos y, de hecho, probablemente nunca necesitarás usar algo tan complejo como el multicoloreado para resolver tales rompecabezas. Pero existen rompecabezas que tienen una solución única, pero no se pueden resolver usando todos los métodos anteriores. Un método que siempre funcionará, aunque de vez en cuando necesita aplicarse nuevamente, es simplemente hacer una suposición y examinar las consecuencias de la suposición. En una situación que parece imposible, elige una casilla que tenga más de un candidato posible, recuerda la situación, haz una suposición para el valor de esa casilla y resuelve el rompecabezas resultante. Si puedes resolverlo, genial, ya terminaste. Si ese rompecabezas no se puede resolver, entonces la suposición que hiciste debe ser incorrecta, puede eliminarse como candidato para esa casilla, y puedes regresar al rompecabezas guardado e intentar resolverlo con un candidato eliminado. Obviamente, cuando intentes resolver el rompecabezas después de haber hecho una suposición, puedes llegar a otra situación en la que se requiera otra suposición, en cuyo caso se debe hacer una segunda suposición de nivel, y así sucesivamente. Pero como el método siempre elimina candidatos, debes llegar a la solución, si hay una. En la ciencia de la computación, esta técnica se conoce como una búsqueda recursiva. La figura 21 es un ejemplo de un rompecabezas que no puede ser resuelto con ninguno de los métodos discutidos hasta ahora, excepto por adivinanza. La solución a este rompecabezas se puede encontrar en la sección 18.
Figura 21: Un Sudoku Muy Difícil
11 Rompecabezas EquivalentesNo hay razón para que los números del 1 al 9 deban usarse para un problema de sudoku. Nunca hacemos ninguna aritmética con ellos: simplemente representan 9 símbolos diferentes y resolver el rompecabezas consiste en intentar colocar estos símbolos en una cuadrícula sujeta a varias restricciones. De hecho, la construcción de una cuadrícula de sudoku completada válida es equivalente a un problema de coloreado de gráficos en teoría de grafos en el siguiente sentido. Imagina que cada una de las 81 casillas es un vértice en un grafo, y hay un borde que conecta cada par de vértices que están en la misma fila, misma columna o mismo bloque. Cada vértice estará conectado a 20 otros vértices, por lo que el grafo de sudoku consistirá en 81 * 20 / 2 = 810 bordes. Encontrar una cuadrícula de sudoku válida equivale a encontrar una forma de colorear los vértices del grafo con nueve colores diferentes de manera que no dos vértices adyacentes compartan el mismo color. Como los símbolos no importan, podríamos usar las letras A a I o cualquier otro conjunto de nueve símbolos distintos para representar lo que esencialmente es el mismo rompecabezas de sudoku. Si tomamos una cuadrícula válida y cambiamos los números 1 y 2, esto es esencialmente el mismo rompecabezas. De hecho, cualquier permutación de los valores del 1 al 9 también generará un rompecabezas equivalente, por lo que hay 9! = 362880 versiones de cada rompecabezas disponibles simplemente reorganizando los dígitos. Si intentas calcular cuántas cuadrículas hay, un buen enfoque sería asumir que la fila superior consiste en los números del 1 al 9 en orden, contar el número de cuadrículas de ese tipo que hay, y luego multiplicar ese resultado por 9! = 362880.
Figura 22: Rompecabezas Esencialmente Equivalentes Además de simplemente reorganizar los números, hay otras cosas que podrías hacerle a un rompecabezas que efectivamente lo dejarían igual. Por ejemplo, podrías intercambiar dos columnas (o filas) de números, siempre que las columnas (o filas) pasen por los mismos bloques. Puedes intercambiar cualquier columna (o fila) de bloques con otra columna (o fila) de bloques. Finalmente, puedes rotar las entradas en una cuadrícula por cualquier número de giros de cuarto de vuelta, o podrías reflejar la cuadrícula a través de una diagonal. La figura 22 muestra algunos ejemplos. Si el rompecabezas de la izquierda es el original, el del centro muestra lo que se obtiene con una reordenación trivial de los dígitos del 1 al 9 (cada 3 en el original fue reemplazado por un 1, cada 1 por un 4, y así sucesivamente). La versión de la derecha también es equivalente, pero es muy difícil ver cómo se relaciona con el rompecabezas de la izquierda. Entonces, una pregunta matemática obvia es, ¿cuántos rompecabezas equivalentes hay de cada cuadrícula de sudoku en el sentido anterior? Otra interesante pregunta matemática surge, y es la siguiente: dado que dos rompecabezas son equivalentes en el sentido anterior, y dado una secuencia de pasos hacia la solución de uno que son seleccionados entre los explicados en capítulos anteriores, ¿esos mismos pasos funcionarán para resolver el otro rompecabezas? En otras palabras, si hay una posición de swordfish en uno, ¿llegaremos a un swordfish diferente en el otro? La respuesta es sí, pero ¿cómo probarías eso? Observa que el rompecabezas de la izquierda (y en el centro) en la figura 22 es simétrico en el sentido de que si marcas las casillas donde aparecen las pistas, siguen siendo las mismas si el rompecabezas se rota 180 grados sobre el centro. Otras versiones de rompecabezas simétricos podrían obtenerse reflejando las casillas de pistas horizontal o verticalmente. La mayoría de los rompecabezas publicados tienen esta forma. Esto no necesariamente los hace más fáciles o más difíciles, pero los hace verse estéticamente mejor, de la misma manera que la mayoría de los crucigramas publicados en los Estados Unidos también son simétricos. Otra pregunta interesante en esto es: dado un rompecabezas simétrico, ¿cuántas versiones equivalentes de él hay?
12 Contando Cuadrículas de SudokuUna cuadrícula de sudoku es un caso especial de un cuadrado latino de 9 × 93 con la restricción adicional de no permitir duplicados en los bloques. Hay muchos cuadrados latinos de 9 × 9: 5524751496156892842531225600. Bertram Felgenhauer ha contado el número de cuadrículas de sudoku únicas usando una computadora, y su resultado ha sido verificado por varias otras personas, y ese número resulta ser mucho menor, pero también enorme: 6670903752021072936960 = 22038571727704267971. Si dividimos el número anterior por 9! obtenemos: 18383222420692992 = 2133427704267971.
13 Cuadrículas de Sudoku Mágicas
Figura 23: Posible Rompecabezas de Sudoku Mínimo Un cuadrado latino tiene todos los dígitos en cada fila y columna. Un "cuadrado mágico" es un cuadrado latino donde cada diagonal también contiene todos los dígitos. ¿Existe tal cosa como una cuadrícula de sudoku mágica? La respuesta es sí, y de hecho hay muchas: 4752, de hecho, si asumimos que la diagonal principal contiene los dígitos en un orden fijo. Las 4752 cuadrículas pueden completarse, y todas de múltiples maneras. El rompecabezas presentado en la figura 23 es un rompecabezas de sudoku estándar, excepto que es más fácil ya que requiere que cada una de las diagonales principales contenga todos los dígitos del 1 al 9.
14 Rompecabezas de Sudoku Mínimos¿Cuántos lugares deben llenarse con números en una cuadrícula vacía para garantizar que haya una solución única? Hasta el momento en que se escribió este documento, la respuesta a esa pregunta aún era desconocida, desconocida, y puede ser que con investigación adicional pueda haber una respuesta definitiva. Se sabe que con 17 pistas hay rompecabezas que tienen soluciones únicas, y no hay ninguno conocido con menos de 17 pistas que tenga una solución única. Un rompecabezas de sudoku mínimo es uno con el menor número posible de pistas para asegurar una solución única. La figura 23 muestra un ejemplo de dicho rompecabezas. Es importante notar que no todos los rompecabezas con 17 pistas tienen soluciones únicas; sin embargo, algunos sí. Determinar la configuración exacta de un rompecabezas de sudoku mínimo puede ser un desafío interesante tanto para los aficionados como para los investigadores de sudoku. En el ejemplo mostrado, cada una de las pistas es esencial para mantener la unicidad de la solución. 3 Un cuadrado latino es una cuadrícula donde la única restricción es que no haya entradas duplicadas en ninguna fila o columna. pero existen ejemplos de rompecabezas que tienen solo 17 ubicaciones llenas que sí tienen una solución única. La figura 14 muestra uno de estos rompecabezas a la izquierda. Aunque este rompecabezas contiene la cantidad mínima de información en términos de pistas iniciales, no es, de hecho, un rompecabezas difícil. El rompecabezas a la derecha en la misma figura contiene 18 pistas y es simétrico. Este es el tamaño más pequeño conocido para un rompecabezas de sudoku simétrico.
Figura 24: Rompecabezas Mínimos
15 Midiendo la Dificultad de los Rompecabezas de SudokuLa dificultad de un rompecabezas de sudoku tiene muy poco que ver con el número de pistas dadas inicialmente. Por lo general, las calificaciones de dificultad se dan para indicar cuán difícil sería para un humano resolver el rompecabezas. Escribir un programa de computadora para resolver rompecabezas de sudoku es casi trivial: solo necesita verificar si la situación actual está resuelta, y si no, hacer una suposición en una de las casillas que aún no se ha llenado, recordando la situación antes de la suposición. Si esa suposición lleva a una solución, genial; de lo contrario, restaura la cuadrícula al estado anterior a la suposición y haz otra suposición. El problema con el esquema de suposiciones es que la pila de suposiciones puede llegar a tener veinte o treinta niveles de profundidad y es imposible para un humano hacer un seguimiento de esto, pero trivial para una computadora. Un método mucho más típico para evaluar la dificultad de un rompecabezas es relativo a los tipos de técnicas de solución que se presentaron en las secciones anteriores de este artículo. En este artículo, las técnicas se introdujeron en un orden que aproximadamente corresponde a su dificultad para un humano. Cualquier humano puede mirar una fila, columna o bloque y ver si hay solo uno faltante y, si es así, resolverlo, etcétera. Así que para probar la dificultad de un problema, un método razonable podría ser este. Intenta, en orden de dificultad creciente, las diversas técnicas presentadas en este artículo. Tan pronto como una tenga éxito, haz ese movimiento y vuelve al comienzo de la lista de técnicas. A medida que avanza la solución, lleva un registro de la cantidad de veces que se utilizó cada técnica. Al final, tendrás una lista de recuentos, y cuanto más veces se utilizó cada técnica (como swordfish, coloreado o multicoloreado), más difícil era el rompecabezas. Las clasificaciones vistas en los periódicos generalmente requieren que el primer grupo de clasificaciones (digamos, principio e intermedio) no utilicen ninguna técnica más allá de aquellas que dan un valor único a una casilla en cada movimiento. En otras palabras, solo utilizan candidatos obvios, solitarios únicos y ocultos para resolver. Los rompecabezas publicados casi nunca requieren adivinanza y retroceso, pero los métodos utilizados para asignar una grado de dificultad varían de un creador de rompecabezas a otro.
16 Recursos en InternetAl momento de escribir este artículo, los siguientes son buenos recursos para sudoku en internet:
17 Rompecabezas de EjemploEsta sección contiene un conjunto de rompecabezas que requieren el uso de técnicas específicas para resolverlos. Así que si deseas practicar con la técnica de coloreado, elige el rompecabezas de coloreado, etcétera. Las soluciones a todos estos aparecen en la sección 18.
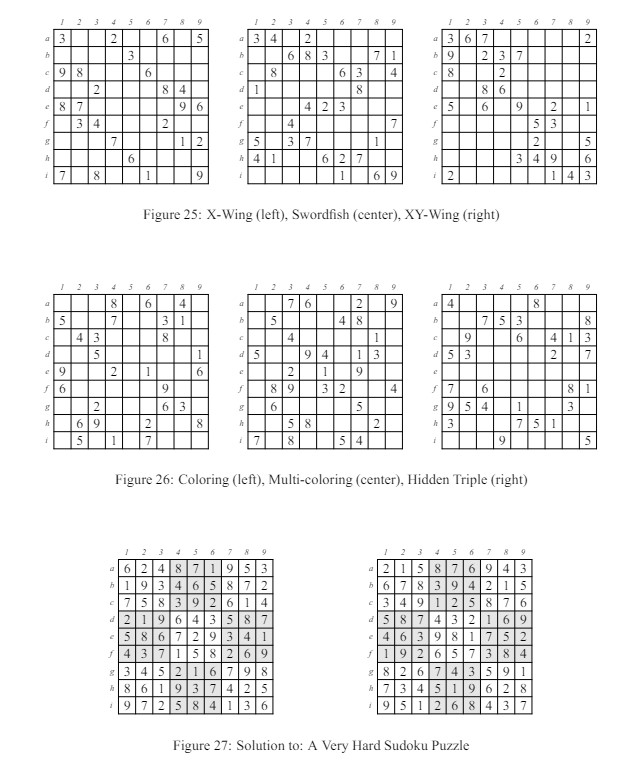
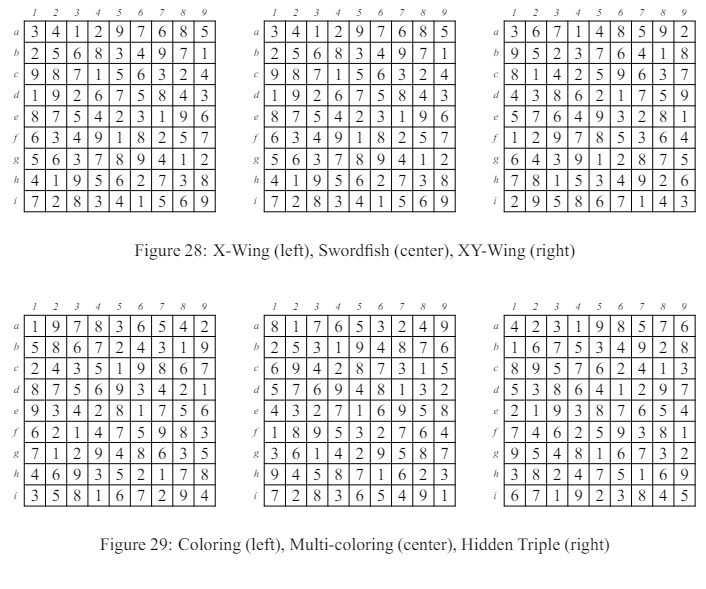
18 SolucionesLa figura 27 es una solución al rompecabezas introductorio en la figura 1 a la izquierda y a la derecha está la solución del rompecabezas extremadamente difícil en la figura 21. Las otras figuras son soluciones a los problemas en la sección 17.
|