|
Suspense en el acantilado Desde donde está parado, un paso hacia el acantilado enviaría al hombre borracho por el borde. Da pasos al azar, ya sea hacia o lejos del acantilado. En cada paso, su probabilidad de dar un paso hacia atrás es de 2/3, la de dar un paso hacia el acantilado, 1/3. ¿Cuál es su posibilidad de escapar del acantilado?
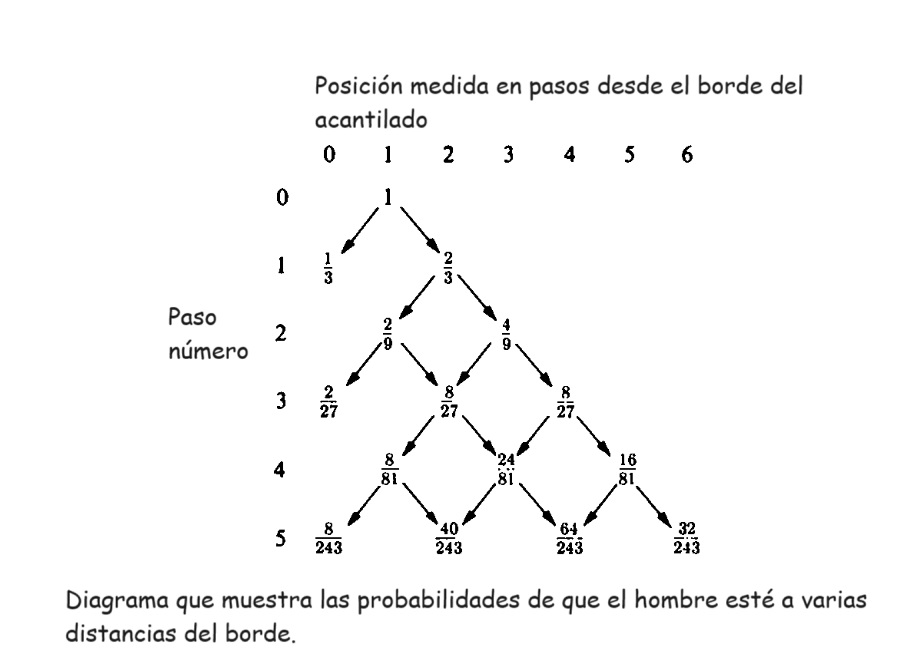
Solución Antes de intentar resolver un problema, encuentro útil ver qué está sucediendo. Veamos qué podría suceder en los primeros pasos. El diagrama ilustra que el hombre solo puede caer por el acantilado en un paso de número impar.
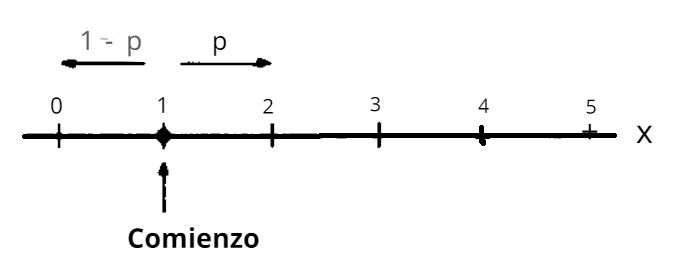
Después de un paso, tenía probabilidad 1/3 de caer por el acantilado. El camino a través de las posiciones 1 → 2 → 1 → 0 agrega otro 2/27 a la probabilidad de desastre para un total de 1. Al final de 5 pasos, los caminos 1 → 2 → 1 → 2 → 1 → 0 y 1 → 2 → 3 → 2 →1→ 0 han agregado juntos 8/243 a la probabilidad de desastre lo que da un total de 107/243 Se podría ampliar la tabla y uno podría aprender algo de un análisis adicional de las probabilidades. Ahora paso a un ataque diferente. Este famoso problema de caminata aleatoria tiene muchas formas. A continuación, lo trataremos como una partícula que se mueve a lo largo de un eje. Consideremos una partícula inicialmente en la posición x = 1 en la recta real. La estructura del problema será más clara si dejamos p, en lugar de 2/3, para la probabilidad de un paso hacia la derecha. La partícula se mueve desde la posición I ya sea hacia la posición x = 2 con probabilidad p o hacia la posición x = 0 con probabilidad 1-p
Más generalmente, si la partícula está en la posición x = n, n > 0, n un entero, su próximo movimiento es hacia x = n + 1 con probabilidad p o hacia x = n-1 con probabilidad 1-p. Si la partícula llega alguna vez a x = 0, se absorbe allí (no da más pasos). Deseamos conocer la probabilidad, P₁, de que la partícula se absorba en x = 0, dado que comienza en x = 1 Naturalmente, el valor de P₁ depende de p. Parece razonable que si p está cerca de 1, P₁ sea pequeño, pero si p está cerca de 0, P₁ esté cerca de 1. Considera la situación después del primer paso: o la partícula se movió a la izquierda x = 0 y fue absorbida (este evento tiene probabilidad 1-p) o se movió a la derecha a x = 2 (este evento tiene probabilidad p) . Sea P2 la probabilidad de que la partícula sea absorbida en x=0 cuando la partícula comienza desde la posición x=2 Podemos escribir (1) P1=1-p+pP2 Pues 1-p es la probabilidad de absorción en el primer paso y pP2 es la probabilidad de ser absorbido después. Los caminos a la absorción desde x=2 se pueden romper en dos partes:
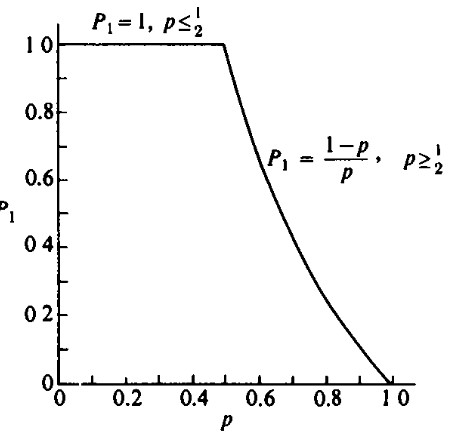
La probabilidad del primer trozo es justo P1 pues la estructura aquí es idéntica a la del conjunto original excepto que el origen se ha desplazado un paso hacia la derecha. La probabilidad de un camino de x = 1 a x = 0 también es P1, porque este es exactamente el problema original. La probabilidad P₂, por lo tanto, es P1², porque los eventos A ( partícula toma camino de x = 2 a x = 1) y B = (partícula toma camino de x = 1 a x = 0) son independientes, y P(A) = P(B) = P1. (Comentario: yo diría que no hace falta considerar que son independiente, pues para medir la probabilidas de que estando en x=2 vaya a x=0, esta es igua a p(B/A) · p(A), es decir probabilidad de que habiendo llegado a x=1 pase a x=0 (p(B/A)) por la probabilidad de que haya llegado de x=2 a x=1 por primera vez ) Podemos reescribir la ec. (1) como P1=1-p+pP1² ecuación cuadrática en P₁ con soluciones P1=1 P1=(1-p)/p En este tipo de problemas, una o ambas soluciones pueden ser apropiadas, dependiendo de las circunstancias. Necesitamos elegir la solución que corresponda a cada valor de p . Cuando p=1/2 , las soluciones coinciden y P1=1 Si p=1, P1=0 porque la partícula siempre se mueve a la derecha Si p=0, solo es válida la solución P1=1 pues P1=1 es un valor entre 0 y 1 Si p<1/2, P1=1 es la única solución válida pues (1-p)/p es ahora mayor que 1 Si p>1/2 , asumiendo que P1 es una función de p continua, entonces la solución válida para llegar a valer 0 en p=1 tiene que ser la 2. Ahora no vamos a demostrar la continuidad que se sale del objeto de este reto. La asumimos. Y P1 es como muestra la imagen
SIMULACIÓN Realizada con chatGPT
Escoge p, la probabilidad de dar un paso alejándose del acantilado, a la
derecha. C es el número de veces que cae al acantilado P da la probabilidad de caer según la p escogida El juego acaba cuando cae al acantilado o cuando ha dado 50 pasos sin haber caído El botón 100 juegos muestra la posición final del último de los cien juegos efectuados
Para dar otra interpretación, si un apostador que comienza con una unidad
de dinero (x=1) pudiera y jugara indefinidamente contra un casino con recursos
infinitamente grandes en un juego justo (p=1/2) en el cual gana o pierde una
unidad en cada jugada, estaría seguro de perder su dinero (P1=1) Que la bancarrota es segura para p =1/2 es sorprendente para la mayoría de nosotros. Normalmente suponemos que si las pruebas de un juego son "justas" (la pérdida promedio es cero), entonces todo el juego es justo. De hecho, esta suposición es generalmente correcta. Si imaginamos este juego, con p=1/2 , jugado infinitas veces, entonces la cantidad promedio de dinero en mano después de n jugadas es 1, para cualquier número finito n. Así que la injusticia es una de esas paradojas del infinito. Otra sorpresa para p=1/2 es que el número promedio de pruebas requeridas para la absorción no es finito. El caso p =1/2 es realmente extraño y profundo. Puede disfrutar aplicando la técnica dada aquí a una partícula que comienza en x = m, en lugar de x = 1, y generalizando los resultados anteriores para mostrar que la probabilidad de absorción desde la posición m es [(1 - p) / p]m o 1 dependiendo de si p es mayor o menor que 1/2 . Cuando p >1/2 y m es grande, es extremadamente plausible que la partícula escape y, por lo tanto, rechazaríamos 1 como la probabilidad de absorción. Si la partícula hubiera comenzado en 0 y se le hubiera permitido dar sus pasos en cualquier dirección con p=1/2 , otro problema clásico de caminata aleatoria preguntaría si la partícula alguna vez regresaría a la posición inicial . Vemos que sí lo haría porque seguramente regresará desde x = 1 y desde x = -1 . Más sobre esto más adelante .
Créditos
Traducción del problema 35 del libro Fifty
challenging problems in probability ,
MOSTELLER
Vídeo introducción con
lumen5.com
Imágenes creadas por chatGPT (DALL-E)
Consolación Ruiz Gil Abril 2024
https://www.matsolin.com/suspense/index.htm
|