|
Test ¿Contestamos al tuntún? ¿Cuántas preguntas?
En los siguientes problemas consideramos un test de n preguntas de las
que estamos seguros de s ¿qué hacemos con las otras? ¿Las contestamos al
tun tún? ¿Las dejamos sin contestar ? Cada pregunta tiene 4 opciones de respuesta y solo una es correcta, los aciertos suman 1 punto, los fallos restan 0,33 puntos. Yo se la respuesta correcta de 4 de ellas, ¿qué hago con las otras 6 de las que no tengo ni idea? ¿respondo al tuntún? ¿cuántas respondo? Quiero sacar un 5 en el test. Solución si no respondo ninguna de las otras 6 p(A)=0 (A = aprobar) 1 si respondo solo una de las otras 6, aprobaré con un acierto, p(A)= (1/4)=25% 2 si respondo solo 2, aprobaré con dos aciertos p(A)= (1/4)^2=6,25% 3 si respondo solo 3, aprobaré con al menos 2 aciertos p(A)=C(3, 2)*(1/4)^2*(3/4)+C(3, 3)*(1/4)^3~15,6% 4 si respondo solo 4, aprobaré con al menos 2 aciertos p(A)=C(4, 2)*(1/4)^2*(3/4)^2+C(4, 3)*(1/4)^3*(3/4)^1+ +(1/4)^4~26% 5 si respondo solo 5, aprobaré con al menos 2 aciertos p(A)=C(5, 2)*(1/4)^2*(3/4)^3+C(5, 3)*(1/4)^3*(3/4)^2+ +C(5,4)*(1/4)^4*(3/4)+(1/4)^5~36,7% 6 si respondo las 6 que quedan, aprobaré con al menos 3 aciertos p(A)= C(6, 3)*(1/4)^3*(3/4)^3+ C(6, 4)*(1/4)^4*(3/4)^2+ +6*(1/4)^5*(3/4)+ (1/4)^6~16,9%
Luego parece que debo responder 5 dejar una en blanco, no es nada buena la probabilidad del 36,7% pero de perdidos al río pues si no lo intento estoy suspensa.
Problema 2: En el test no se trata de aprobar o no, el objetivo es sacar cuantos más puntos mejor. El test tiene n preguntas, yo se responder bien con seguridad r y del resto no se cuantas debo contestar. Cada pregunta tiene 4 opciones de respuesta y solo una es correcta, los aciertos suman 1 punto, los fallos restan 1/3 de punto. Ahora no busco aprobar sino saber si contestar algunas al tuntún me ayudará a conseguir algún punto más o si por el contrario al hacerlo fastidiaré la nota que ya tengo con seguridad. Caso 1: no tengo ni idea de las preguntas que no sé Solución Supongamos que contesto c preguntas al tuntún, si el número de aciertos que tendré es a, los fallos serán c-a y la puntuación que añado, a-(c-a)·1/3 Busco que esta puntuación sea positiva porque para quedarme como estoy o arriesgarme a perder puntos no contesto más, por tanto a>c/4 Quiero saber la probabilidad de que el número de aciertos sea mayor que c/4. Esto es una binomial B(c, 1/4) Y la probabilidad buscada es B(c, 1/4)>c/4 (notación de Wolfram Mathematica) Pongamos esto en la calculadora, en este caso
cogeremos una hoja de cálculo, y ver el valor de esta expresión para distintos
valores de c.
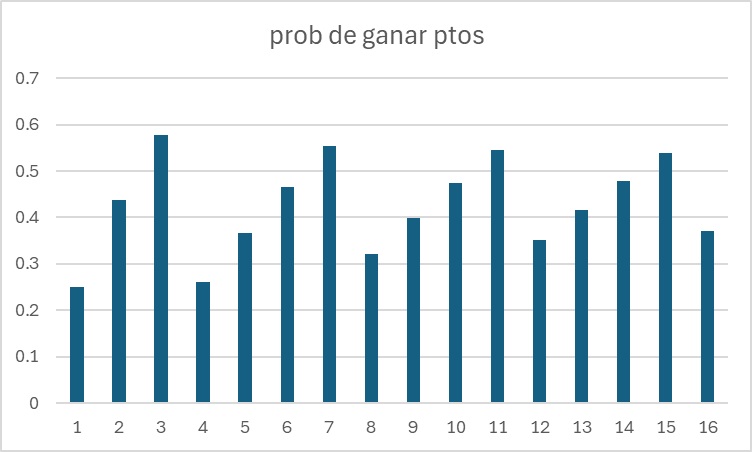
Gráfica
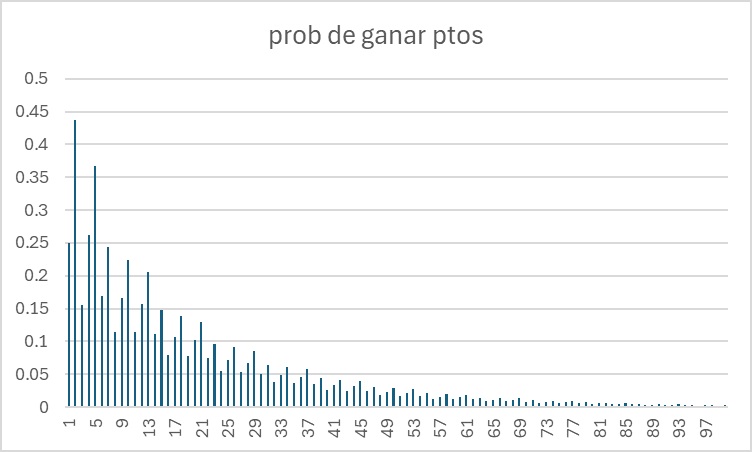
Está claro que debo coger c de manera que al dividirlo entre 4 de un resto igual a 3 Gráfico con c de 1 a 100
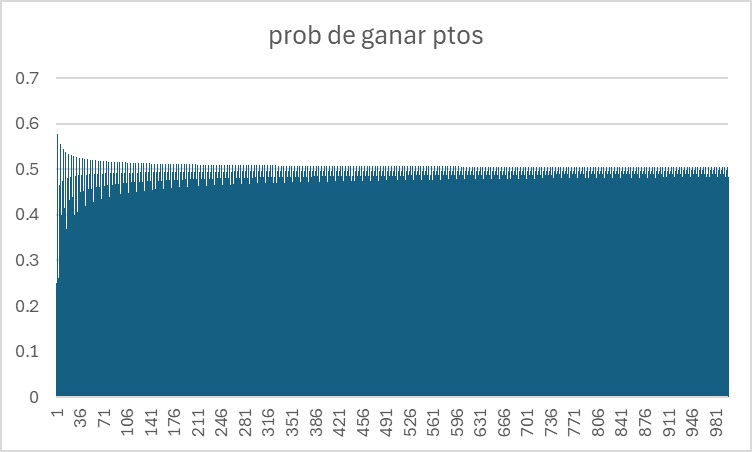
Gráfico con c de 1 a 1000
Caso 2 hay algunas preguntas en las que
dudo entre dos opciones En este caso si contestara c de estas al
tuntún estaría en una binomial B(c, 1/2)>c/4
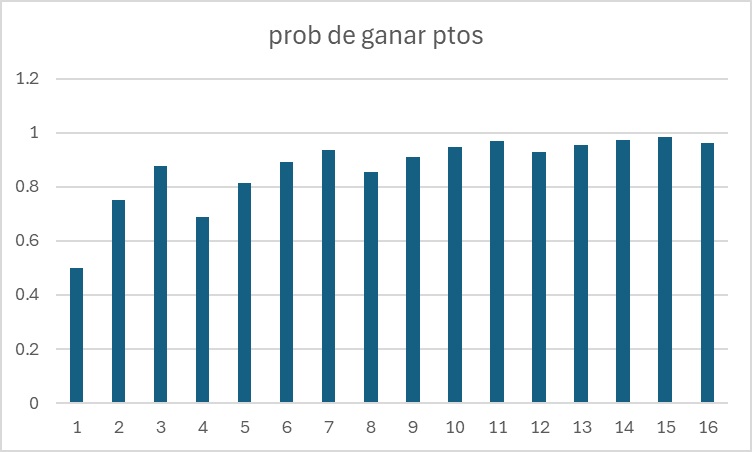
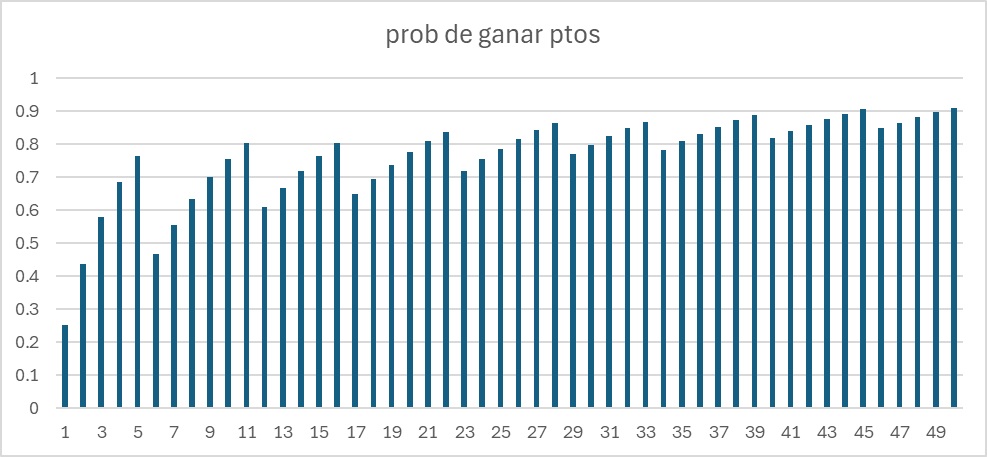
Veamos el gráfico hasta 100
La cosa cambia, está claro que las preguntas en las que dude entre dos debo contestarlas al tuntún en lugar de dejarlas en blanco, salvo que solo dude en una.
Caso 3 hay algunas preguntas en las que dudo entre tres opciones Hay preguntas en las que con toda seguridad una de las respuestas es falsa. ¿Cuántas de estas debo contestar para tener más probabilidad de ganar puntos? En este caso si contestara c de estas al
tuntún estaría en una binomial B(c, 1/3)>c/4
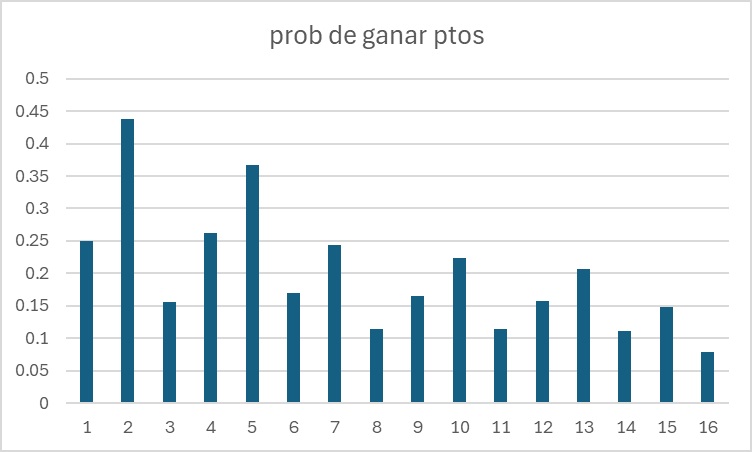
Veamos el gráfico hasta 100
Pues también hay bastante probabilidad de sacar más puntos si las contesto al tuntún, y observamos que siempre funciona la regla del máximo con resto 3 al dividir c entre 4. Paréntesis, lo que va en gris es eso, un paréntesis, se puede saltar Esta regla de un máximo cada 4 se debe a que el fallo resta 1/3, si el fallo restara 1/7 entonces sería un máximode cada 8 y el máximo estaría en los múltiplos de 8 menos 1
Y esto que sigue ocurre cuando cada fallo resta 3/5 de punto (3,3,2)
En la siguiente tabla se indica el patrón que sigue esta gráfica para diversos valores de lo que reste cada fallo
Por ejemplo si cada fallo resta 3/14 puntos, la gráfica sigue el patrón 6 6 5 como se ve aquí abajo
Es curioso, y si vemos una gráfica de
patrón 5 5 6 ya sabemos que en ella cada fallo resta 3/13 (3
porque es un patrón de 3 elemento, y 13 porque al primero le
quito 3 , queda 2 y lo sumo con los otros, 5 y 6.
3/(12+ 15 +16) Fin del paréntesis
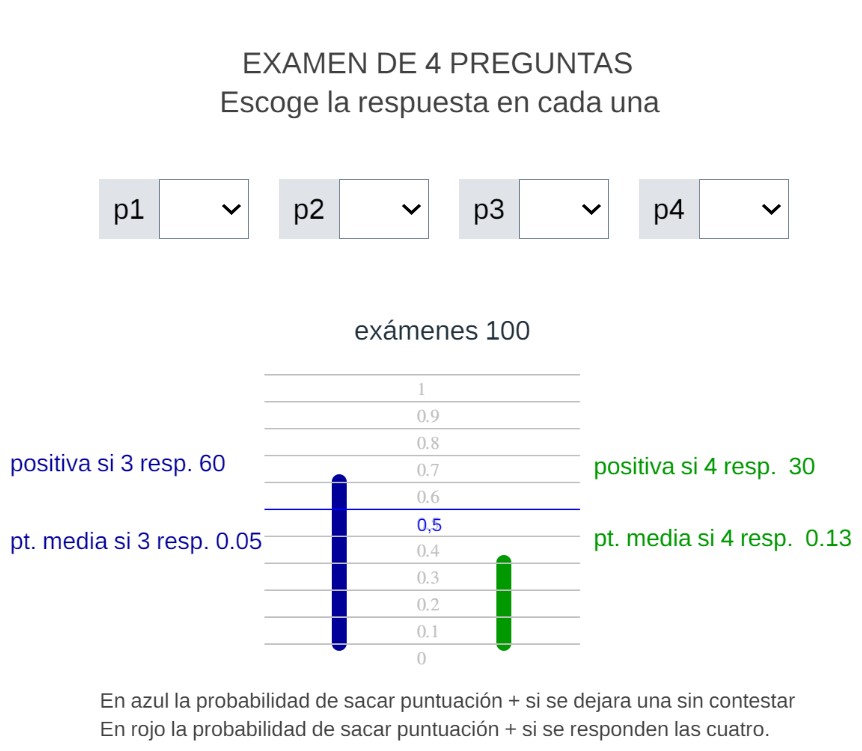
Dejamos dos capturas del resultado después de hacer cien exámenes al tuntún, las barras muestran la probabilidad de sacar puntuación positiva cuando respondo solo tres preguntas (barra verde) y cuando respondo las cuatro (verde)
Ha salido, como era de esperar, practicamente lo mismo que las barras 3 y 4 de la gráfica del caso 1.
Consolación Ruiz Gil Febrero 2024 https://www.matsolin.com/test/index.htm
|