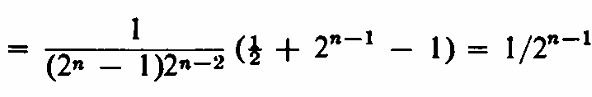|
Caballeros gemelos (a) Supongamos que el Rey Arturo realiza un torneo de justas donde las justas son por parejas como en un torneo de tenis. Ver Problema del subcampeón. Los 8 caballeros en el torneo son igualmente habilidosos, e incluyen a los caballeros gemelos A y B. ¿Cuál es la probabilidad de que los gemelos se encuentren en un partido durante el torneo?
Aquí puedes ver la probabilidad de encontrase A y B en la simulación anterior, pues se registran los resultados de cualquier usuario. ( b ) Reemplazar 8 por 2n en el problema anterior . Ahora, ¿cuál es la probabilidad de que se encuentren?
Solución ( a ) Designar a los gemelos como A y B. Colocar a A en el primer brazo ( primera línea de la escalera ) . Entonces B está en el mismo brazo ( par de líneas ) , o en el siguiente , o en la mitad inferior . La probabilidad de que B esté junto a A es 1/7 , y entonces la probabilidad de que se encuentren es 1. La probabilidad de que B esté en el siguiente par a A es 2/7 , y entonces la probabilidad de que se encuentren es 1/4 , porque , para encontrarse , cada uno debe ganar su primer partido . Finalmente , la probabilidad de que B esté en la mitad inferior es 4/7 , y entonces su probabilidad de encontrarse es 1/24 = 1/16 porque ambos deben ganar 2 partidos . Por lo tanto la probabilidad total de que se encuentren es : 1/7·1 + 2/7·1/4 + 4/7·1/16 = 1/4 ( b ) Notar que para un torneo de tamaño 2 es seguro que se encuentren . Para 22 = 4 partici pantes , su probabilidad de encontrarse es 1/2 ; para 2³ = 8 participantes , hemos calculado su probabilidad de ser 1/4 = 1/22 . Por lo tanto, una conjetura razonable es que para un torneo de tamaño 2 " , su probabilidad de encontrarse es 1/2n-1 . Vamos a demostrar esta conjetura por inducción . Consideremos primero el caso en el que los caballeros están en mitades opuestas de la escalera, luego el caso en el que están en la misma mitad . La probabilidad de que tanto A como B estén en mitades opuestas de la escalera es 2n-1 / ( 2n– 1 ) , como sabemos del problema del tenis im- mediatamente anterior . Si están en mitades opuestas, A y B solo pueden encontrarse en la final . Un caballero tiene una probabilidad de 1/2n-1 de llegar a la final porque debe ganar n - 1 justas . La probabilidad de que tanto A como B lleguen a la final ( 1/2n-1 ) ² = 1 / 22n-2 . Por lo tanto, la probabilidad de que estén en mitades opuestas y se encuentren es [ 2n-1 / ( 2n– 1) ] ( 1 / 22n-2) . A esta probabilidad se debe agregar la probabilidad de que estén en la misma mitad y se encuentren . Su probabilidad de estar en la misma mitad es ( 2n-1- 1 ) / ( 2n– 1 ) , y según la hipótesis de inducción, su probabilidad de encontrarse en una torneo de n-1 rondas es 1/2 n-2 . Si la hipótesis de inducción es verdadera , su probabilidad total de encontrarse es [ 2n-1 / ( 2n– 1) ] ( 1 / 22n-2) + ( 2n-1- 1 ) / ( 2n– 1 ) ·(1/2 n-2 )=
que era la hipótesis de inducción que esperábamos verificar . Eso completa la inducción .
Créditos
Vídeo introducción con
lumen5.com
Simulación realizada por chatGPT
Consolación Ruiz Gil Abril 2024
https://www.matsolin.com/caballeros/index.htm
|