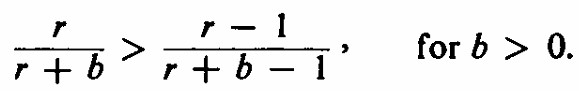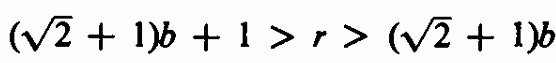|
El cajón de los calcetines Bienvenido al fascinante mundo del cajón de los calcetines, donde la probabilidad y la lógica se entrelazan en un desafío intrigante. En este misterioso cajón, se ocultan calcetines rojos y blancos, desafiando nuestra intuición y habilidades matemáticas. ¿Cuántos calcetines necesitamos tener en este cajón para que la probabilidad de extraer dos calcetines rojos al azar sea exactamente del 50%? Este enigma, extraído del libro "Fifty challenging problems in probability" de Frederick Mosteller, nos invita a explorar las complejidades de la probabilidad y encontrar la solución óptima. Acompáñanos en este viaje de descubrimiento y desafía tu mente con este intrigante acertijo. Un cajón contiene calcetines rojos y calcetines blancos. Cuando se extraen dos calcetines al azar, la probabilidad de que ambos sean rojos es 50%. (a) ¿Cuál es el menor número de calcetines en el cajón para que la probabiblidad de sacar dos rojos sea 1/2? (b) ¿Y si el número de calcetines blancos es par? (Fifty challenging problems in probability. Frederick Mosteller) Solución sean b y r el número de calcetines blancos y rojos respectivamente, la probabilidad de que ambos sean rojos es
Y teniendo en cuenta que
podemos escribir las desigualdades
Y operando concluimos que
Luego el menor r es cuando b=1 y el único r con las desigualdades anteriores y b=1 es r=3 Con estas dos desigualdades también se concluye que la probabilidad de dos rojo nunca puede ser 1/n2 pues quedaría (n+1)b+1>r>(n+1)b y no hay ninún número natural entre dos naturales consecutivos.
(b) ¿Y si el número de calcetines blancos es par? Construyamos la tabla
Así que el menor r es r=15 b=6
Si quisiéramos saber el siguiente valor de r (aunque b no par) con esta
probabilidad igual a 1/2 estaríamos ante un problema de teoría de
números y ello nos llevaría a la ecuación diofántica de
Pell , los siguientes valores son r=85 b=35 Hasta aquí se ha puesto una casi copia o traducción del artículo de Mosteller Ahora en una hoja de cálculo hemos puesto los posibles valores de la probabilidad de sacar al menos dos calcetines rojos cuando en el cajón se meten entre 2 y 10 calcetines rojos y entre 1 y 100 blancos,
Vamos a ordenarla según r
Está claro en estos casos que cuando r/b>=3, p>=1/2 La pregunta que ahora surge es ¿será esto cierto para cualquier r y cualquier b aunque no sean menores que 10 y 100? Cierto, pues p como función de r, f(r), para una b determinada es una función creciente , producto de dos funciones crecientes. luego si r>=3b, p= f(r)>=f(3b)=3/4 · (3b-1)/(4b-1) Y esta última función, como función de b también es creciente, así que teniendo en cuenta que b>=1, 3/4 · (3b-1)/(4b-1) >= 3/4 · (3-1)/(4-1) = 1/2 Hemos visto que
¿Y el recíproco? ¿si r<3b, p<1/2? es decir ¿si r<=3b-1, p<1/2? Pues no, en la tabla tenemos el contraejemplo r=8 b=3 Mosteller nos dió más contraejemplos r=15 b=6 r=85 b=35 Volviendo a la hoja de cálculo (r<=10, b<=100) nos fijamos en los valores que dan una probabilidad de dos rojos mayor o igual que 1/3
Si nos fijamos en r/b:
observamos que r/b es siempre mayor que 3/2 p como función de r, f(r), para una b determinada es una función creciente, producto de dos funciones crecientes. luego si r>=3/2 b, p= f(r)>=f(3/2 b)=3/5 · (3/2 b-1)/(5/2 b-1) Y esta última función, como función de b también es creciente, así que teniendo en cuenta que b>=1, 3/5 · (3/2 b-1)/(5/2 b-1) >= 3/5 · 1/3 = 1/5 Vemos ahora que
Busquemos una fórmula general Si r/b>=c , p>=¿? una mera sustitución, con el mismo procedimiento anterior nos demuestra que
PROBLEMA 2 Planteemos ahora otro problema con tres colores de calcetines
Tenemos 16 calcetines blancos, 12 negros, 18 rojos ¿Cuál es el número mínimo de calcetines que tengo que sacar sin mirar para saber que voy a tener un par de calcetines del mismo color? Y, la segunda: ¿cuántos calcetines tendría que sacar del cajón a oscuras, sin mirar, para estar seguro de tener un par rojo?
Solución Para tener un par del mismo color bastaría con sacar 4 calcetines, porque si se sacan 3, puede que sea uno de cada color, el cuarto ya repetiría. Para estar seguro de que salga un par rojo, habrá que sacar 30 calcetines, porque a puede pasar que salgan todos los blancos (16) y todos los negros (12) que suman 28, si se sacan 30 ya habrá al menos dos rojos.
Saquemos más jugo al problema. Estoy dispuesto a ir uno de cada dos días sin dos calcetines rojos, es decir, me da igual que el 50% de los días me vean sin dos calcetines rojos, porque otro 50% de los días me verán elegantemente vestido con mis dos calcetines rojos. La pregunta es ¿cuántos calcetines debo sacar para ir con mis dos calcetines rojos el 50% de los días. Solución Si saco x calcetines quiero que la probabilidad de que no haya dos rojos sea menor que 1/2, así habrá dos rojos más del 50% de las veces. Esta probabilidad es igual a
la probabilidad de no sacar dos rojos es
Si x=2 esa probabilidad es 28 / 46 · 63 / 45 = 0,85217... Si x=3 esa probabilidad es 28 · 27 / (46 · 45) · 80 / 44 = 0.6640... Si x=4 esa probabilidad es 28 · 27 · 26 / (46 · 45 · 44) · 97 / 43 = 0.4868... menor del 50% que es lo que buscábamos Luego tendré que sacar cuatro calcetines para que el 50% de los días vaya bien elegante con dos calcetines rojos. En esta calculadora se simulan x extracciones de y calcetines, una extracción cada día.
CRÉDITOS Fifty challenging problems in probability. Frederick Mosteller Reto matemático de onda cero dirigido por José Ángel Muncia el 30 de junio de 2020 (Programa Más de uno).
AGRADECIMIENTOS
Equipo Descartes, por las imágenes y sugerencias,
un gran equipo docente.
Consolación Ruiz Gil Febrero 2024 https://www.matsolin.com/calcetines/index.htm
|