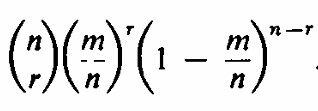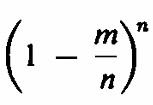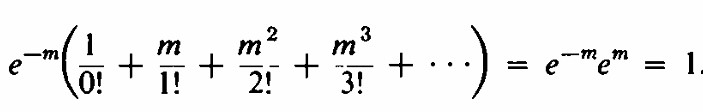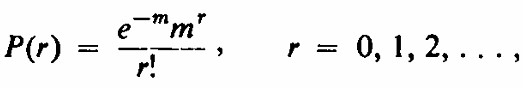|
Atrapando al falsificador codicioso El acuñador del rey coloca sus monedas n en una caja. Cada caja contiene m monedas falsas. El rey sospecha del acuñador y saca al azar una moneda de cada una de las n cajas y las hace probar. ¿Cuál es la probabilidad de que la muestra de n monedas contenga exactamente r falsas? Solución Cada una de las monedas en la muestra del rey se extrae de una caja nueva y tiene una probabilidad m / n de ser falsa. Las extracciones son independientes, y por lo tanto obtenemos la probabilidad binomial para r falsas y n-r verdaderas
Veamos qué sucede cuando n crece mientras que r y m están fijos. Escribimos P (r monedas falsas) como
A medida que n crece, 1 / r! no cambia, mr no cambia,
cada uno es estos dos factores tienden a 1 y
tiende a e-m De modo que la probabilidad de r monedas falsas cuan n crece tiende a
Estos términos suman 1 , es decir para r de 0 a infinito
el paréntesis es la expansión en serie de potencias de em Distribución de Poisson La distribución cuyas probabilidades son
se llama distribución de Poisson y representa el comportamiento probabilístico de muchos procesos físicos . Puede leer sobre la distribución de Poisson en M. J. Moroney , Datos de cifras , 3ª ed. , Penguin Books , Ltd. , Baltimore , Maryland , 1956 , pp . 96-107 . 2 8 23
SIMULACIÓN CON CHATGPT
A continuación se simula con chat GPT la robabilidad de obtener exactamente r monedas falsas en una extracción la probabilidad teórica si n es grande es
SIMULACIÓN 2 CON CHATGPT
Créditos
Vídeo introducción con
lumen5.com
Simulación realizada por chatGPT
Consolación Ruiz Gil Abril 2024
https://www.matsolin.com/codicioso/index.htm
|