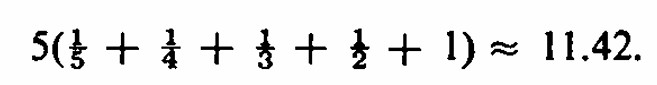|
Recopilando cupones Constante de
Euler-Mascheroni ϒ Los cupones en las cajas de cereales están numerados del 1 al 5 , y se necesita conseguir los 5 números obtener un premio . Con un cupón por caja , ¿cuántas cajas en promedio se necesitan para completar un conjunto completo?
se ve el promedio conseguido por todos los usuarios que van entrando en esta página y participan en la simulación del problema. Solución Obtenemos uno de los números en la primera caja. Ahora la el promedio de cajas abiertas para obtener un nuevo número de la siguiente caja, usando el resultado del problema Primer 6 es 1/(4/5) = 5/4 Cuando ya tenemos dos números diferentes, el promedio de cajas necesarias para obtener el tercer número es
1/(3/5) = 5/3
Aproximación de Euler para los términos de la serie armónica Si la serie de cupones fuera más larga, n números diferentes, sería conveniente utilizar la constante de Euler-Mascheroni
El 0.57721 ... se conoce como la constante de Euler . El primer miembro es el término n-ésimo de la serie armónica. Para n cupones en un conjunto , el número promedio de cajas es aproximadamente n logen + 0.577 n + 1 . Dado que loge5 es 1.6094 , la aproximación de Euler para n = 5 da como resultado 11.43, muy cerca de 11.42 . A menudo omitimos el término 1/2n en la aproximación de Euler
Créditos
Vídeo introducción con
lumen5.com
Simulación realizada por chatGPT
Consolación Ruiz Gil Abril 2024
https://www.matsolin.com/cupones/index.htm
|