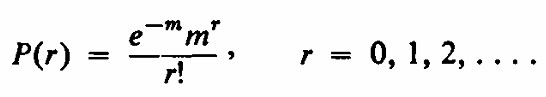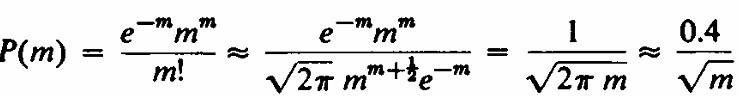|
Gelatina mohosa Las esporas en el aire producen pequeñas colonias de moho en placas de gelatina en un laboratorio . Las muchas placas tienen un promedio de 3 colonias por placa . ¿Qué fracción de placas tiene exactamente 3 colonias ? Si el promedio es un número entero grande m, ¿qué fracción de placas tiene exactamente m colonias?
Solución Considere la superficie de una placa como dividida en n pequeñas áreas iguales . Para cada área, la probabilidad de una colonia es p , pero el número medio es np = 3 . Queremos áreas pequeñas . A medida que n crece , p se vuelve pequeño , porque el área de una subregión tiende a cero . En lugar de fijarnos en un número promedio de 3 , mantengamos un promedio general , m = np. Es posible que te preocupes de que en algunas áreas puedan ocurrir 2 o más colonias , pero tranquilo , porque las regiones pequeñas serán tan pequeñas que apenas podrán contener una colonia. Entonces la probabilidad de exactamente r colonias en n áreas pequeñas es la binomial
donde p= m/n Reemplaza p por m/n.Entonces,la fórmulaes nuestro viejo amigo del Falsificador Codicioso , Problema 28. Dejemos que n tienda a infinito , y nuevamente obtenemos la distribución de Poisson
Para m=3 , y r = 3 , esto da como resultado 0.224 . Puedes verificar a partir de la definición que m es el promedio de la distribución de la siguiente manera :
Actualmente hay varias buenas tablas de la distribución de Poisson:
Para obtener los resultados para un valor grande de m, donde r = m, podríamos usar las tablas o aplicar la aproximación de Stirling. La aproximación de Stirling da
Ejemplos numéricos:
SIMULACIÓN CON CHATGPT
del problema 28
Créditos
Traducción del problema 29 del libro Fifty
challenging problems in probability ,
MOSTELLER
Vídeo introducción con
lumen5.com
Simulación realizada por chatGPT
Consolación Ruiz Gil Abril 2024
https://www.matsolin.com/gelatina/index.htm
|