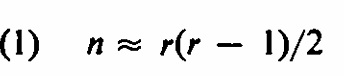Si r personas comparan cumpleaños en el problema de las parejas, la probabilidad de que al menos 2 tengan el mismo cumpleaños es Pr.

¿Cuánto deb valer n en el problema personal de encontrar compañero de nacimiento para que tu probabilidad de éxito sea aproximadamente Pr?

Solución

Por ejemplo, cuando r = 23,

n debería ser aproximadamente

23 (22) / 2 = 253,

lo cual concuerda exactamente con nuestros hallazgos en los dos problemas anteriores.

Aquellos que deseen profundizar en esto podrían ver "Entendiendo el problema del cumpleaños", Maestro de Matemáticas, Vol. 55, 1962, pp. 322-5.

En los dos problemas anteriores encontramos que, para n mucho menor que N (N=365), la probabilidad de no encontrar a su compañero de nacimiento entre n personas es aproximadamente

e^{-n / N}.

De manera similar, encontramos en el problema de las parejas de cumpleaños que, para valores pequeños en comparación con N, la probabilidad de no encontrar una pareja con cumpleaños idénticos es aproximadamente

e ^{- r (r-1 ) / 2N.}

Para que las dos probabilidades sean casi iguales,

la expresión (1) debe cumplirse. Este ataque directo a través de la aproximación nos da una forma de entender la relación entre los problemas. La discusión anterior deja claro que

r ( r - 1 ) / 2

tiene la interpretación física "número de oportunidades" que proporcionó otra explicación para comparar n con

 r ( r − 1 ) / 2.