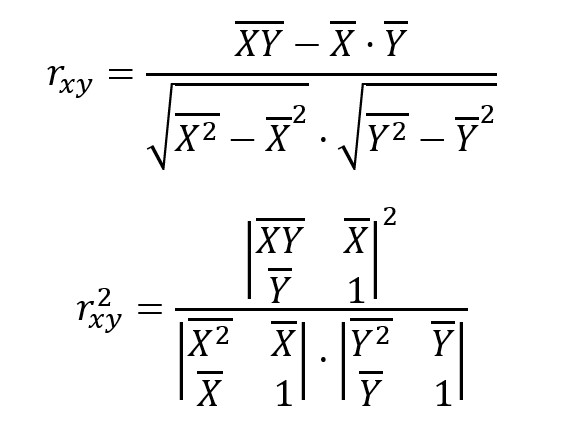
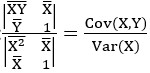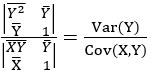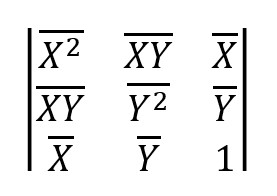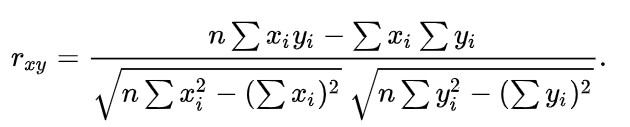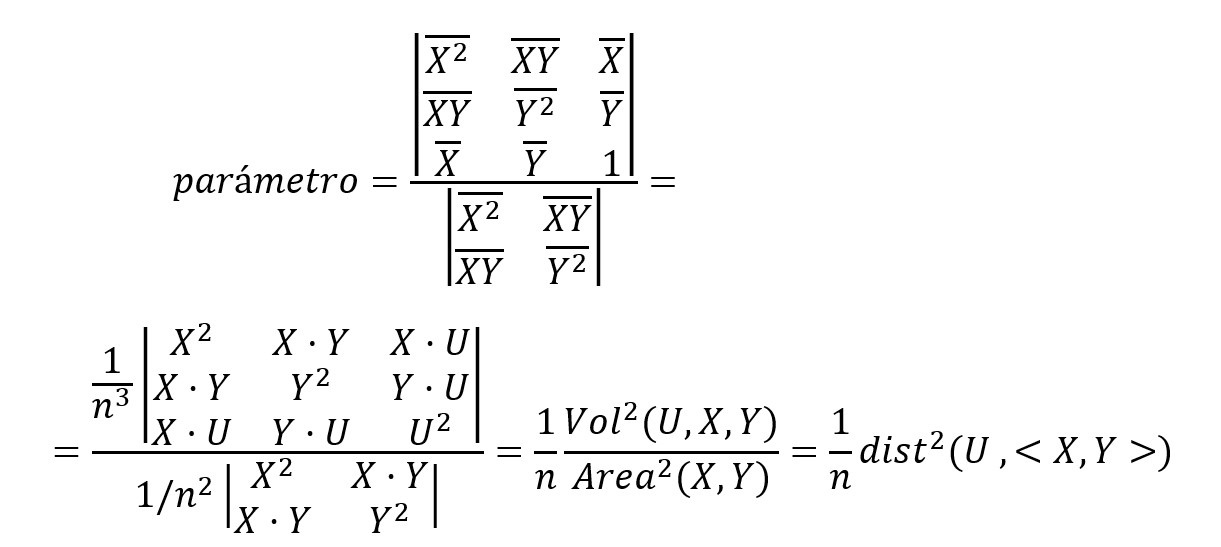Recta de regresión

Consideremos dos vectores en IR^m, X, Y vamos a calcular las rectas de regresión de X e Y, aX+bY=U  siendo U= ( 1, … , 1 )

Por tanto la pendiente de esta recta de regresión de Y/X  es   -a/b:

Por tanto la pendiente de esta recta de regresión de Y/X  es   -a/b:

Por tanto la pendiente de esta recta de regresión de Y/X  es   -a/b:

Los métodos de los mínimos cuadrados para el módulo de Y- f(X) siendo y=f(x) la ecuación de una recta, da la primera recta; si hacemos el método de mínimos cuadrados para el módulo de X-g(Y), siendo g la ecuación de la recta, da la segunda recta. Y la tercera no se suele tomar.

¿Cómo es esa tercera recta?

Si pensamos en los tres vectores U, X, Y la primera recta es el vector combinación lineal de U y X cuya distancia a Y es mínima (mínimos cuadrados), el resultado es el pie de la perpendicular desde Y a <U X>, esto es lo que hace el método de los mínimos cuadrados, y es lo que hacemos con las ecuaciones pues este pie al estar en <U X> es de la forma mX+nU y al restárselo a Y es perpendicular a U y  a X de modo que

(mX+nU-Y)·U=0

(mX+nU-Y)·X=0

es decir, la recta aX+bY-U=0 se esta multiplicando por U y por X

La segunda recta es la combinación lineal de U, Y cuya distancia a X es mínima, que es el pie de la perpendicular desde X a <U Y>

¿Y la tercera recta? ¿Es el pie de la perpendicular desde U a <X Y>?

Supongamos que el pie de la perpendicular desde U al plano <X Y> es aX+bY, entonces
U-aX-bY, es perpendicular a X y a Y,
U·X-aX·X-bY·X=0

U·Y-aX·Y-bY·Y=0
que son justo las ecuaciones (1) y (3) , ahora es fácil entender que el método de los mínimos cuadrados y el de resolver los tres sistemas anteriores coinciden.

Un coeficiente para medir cuando y cuanto se aproxima la nube de puntos de los pares (xi, yi) a una recta, es el siguiente determinante:

Pues está claro que forman una recta si el elemento de volumen de U, X, Y es cero, entonces cuanto más cerca de cero esté este elemento, más cerca se estará de que los tres vectores sean coplanarios.  El determinante es igual a

1/n³·Vol²(U,X,Y).

Este determinante lo vemos calculado en las siguientes escenas así como el coeficiente de correlación lineal

que dividiendo por n² el numerador y el denominador resulta,

Calculamos otro parámetro, al tomarlo se está pensando en la distancia de U a <X, Y>, pero como para el cálculo tomamos las medias y el elemento de volumen al cuadrado, este será igual al cuadrado de esa distancia dividido por n

X·Y es la suma de los xi·yi, y si tomo la media estoy dividiendo esa suma por n, es decir X·Y/n

esta distancia de U a  <X, Y>)será menor que el módulo de U, raiz de n, por ello el nuevo parámetro sale menor que 1

En la escena se generan dos vectores X, Y en IR²⁰ , el punto naranja es el de sus medias y vermos dibujadas las tres rectas anteriores, hay veces que X e Y son casi proporcionales, entonces la recta amarilla se separa mucho de las otras dos.

Este último parámetro entre 0 y 1 indica que la nube es casi una recta cuando es casi 0 y cuando es casi 1 habrá mucha dispersión.

Esta interpretación geométrica de los parámetros es interesante, pues por ejemplo la varianza de X es
 

La media de X es el producto escalar X·U dividido entre n, es decir el X·U/U·U

Estos determinantes de orden n cuyos términos son productos escalares de   vectores con n coordenadas son iguales a la suma de los menores al cuadrado de la matriz definida por esos vectores, por tanto la varianza es igual también  1/n² · suma de los (xi-xj)².

Vease regresion 2