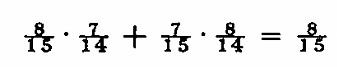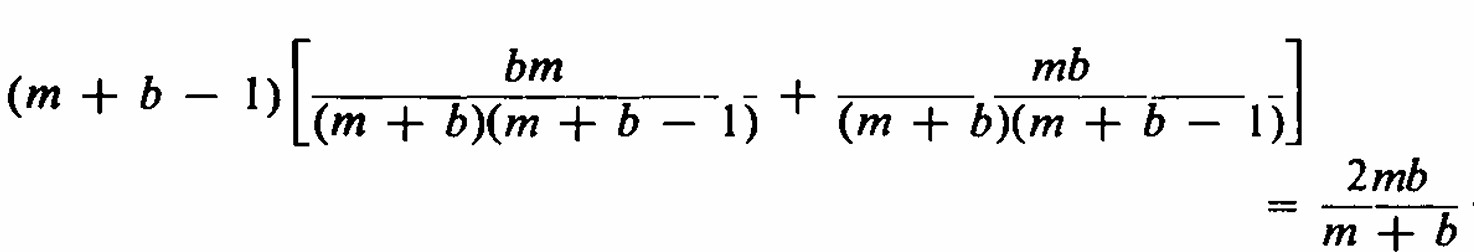La fila del teatro

Ocho hombres y 7 mujeres compraron aleatoriamente asientos individuales en la misma fila de 15 asientos de un teatro .

¿En promedio , cuántas parejas de asientos adyacentes están reservadas para parejas mixtas?

Solución

La secuencia podría ser ( B para soltero , M para modelo )

HHMMHHMHMHMHHMM,

y ocurren 9 pares de HM o MH.

Queremos el número promedio de pares adyacentes diferentes. Para que sean diferentes, debemos tener HM o MH.

La probabilidad de una pareja mixta en los primeros dos asientos es

Mira las primeras dos posiciones. Si son diferentes, obtenemos una pareja mixta, si son iguales, obtenemos cero. Como la probabilidad de pareja mixta es 8/15

8/15·(1)+7/14·(0)

Concluimos que 8/15  es también la media al contar el número de parejas mixtas en las dos primera butacas.

Este mismo cálculo se aplica a cualquier par adyacente. Como son 14 pares adyacentes, pues el promedio de pares mixtos será la suma de 8/15 catorce veces

14·8/15

Más general, con b elementos de un tipo y m de otro, dispuestos aleatoriamente en una línea, el número esperado de elementos adyacentes diferentes es

En nuestro ejemplo b= 8 , m = 7 , dando

14·8/15

El teorema clave utilizado aquí es que el promedio de una suma es la suma de los promedios . Encontramos el número promedio de parejas mixtas en cada posición , en el ejemplo y los sumamos para cada par adyacente.

Se presenta una derivación de este teorema en PWSA pp . 214–216