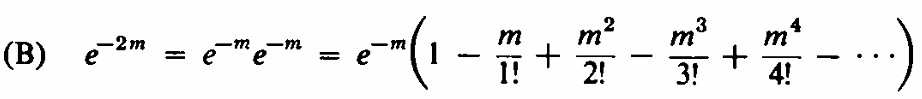|
Igualando las ventas Un vendedor de pan vende en promedio 20 pasteles en una ronda de su ruta. ¿Cuál es la probabilidad de que venda un número par de pasteles? (Suponemos que las ventas siguen la distribución de Poisson.)
Solución ¿Por qué asumir una distribución de Poisson? En parte porque el problema queda bien de esa manera. En parte porque la distribución puede ser cercana a una distribución de Poisson debido a que el vendedor tiene muchos clientes, cada uno con una pequeña probabilidad de comprar un pastel. Puede que te preocupes por la variación de un día a otro durante la semana, lo cual está bien —yo solo estoy pensando en los martes de verano. La mayoría de nosotros adivinaría sobre eso la probabilidad de vender un número par en un día es 1/2. La probabilidad de que él venda exactamente r pasteles es e - 2020r / r !, como sabemos del Problema 28. Trabajar con la media general m en lugar de 20 aclarará la estruc tura del problema. Entonces, la suma de las probabilidades de Poisson es
Queremos eliminar los términos correspondientes a números impares de pasteles. Recuerde que
La suma de las expresiones ( A ) y ( B ) nos daría el doble de la probabilidad de un número par de panes, porque los términos con potencias impares de m se anulan y los términos con potencias pares tienen un coeficiente de 2. Consecuentemente, después de dividir por 2, obtenemos la probabilidad de un número par (1+e-2m)/2. Para m=20 el resultado es extremadamente cercano a 0.5 porque e-40 es despreciable.
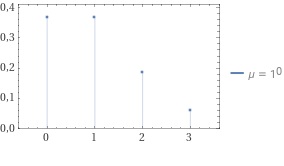
Por otro lado, si vende en promedio una tarta especial de cumpleaños por viaje en la ruta, la probabilidad de vender un número par de tartas especiales de cumpleaños es aproximadamente 0.568
Créditos
Traducción del problema 30 del libro Fifty
challenging problems in probability ,
MOSTELLER
Vídeo introducción con
lumen5.com
Imágenes creados por chatGPT (DALL-E)
Consolación Ruiz Gil Abril 2024
https://www.matsolin.com/ventas/index.htm
|