Victorias sucesivas

Para alentar la prometedora carrera tenística de Elmer, su padre le ofrece un premio si gana (al menos) dos sets seguidos de tenis en una serie de tres sets alternativamente con su padre y el campeón del club: padre-campeón-padre o campeón-padre-campeón, según la elección de Elmer. El campeón es mejor jugador que el padre de Elmer. ¿Qué serie debería elegir Elmer?
Solución

Dado que el campeón juega mejor que el padre, parece razonable que se jueguen menos sets con el campeón. Por otro lado, el set del medio es clave, porque Elmer no puede tener dos victorias seguidas sin ganar el del medio.

Sea C el campeón, P el padre y  G y D la victoria y la derrota de Elmer.

Sean

p la probabilidad de que Elmer le gane cualquier set a su padre,

c la probabilidad correspondiente de ganarle al campeón.

La tabla muestra las únicas secuencias posibles de premio junto con sus probabilidades, dada la independencia entre conjuntos, para las dos elecciones.

Contra Padre 1º   Contra el Campeón 1º
P C P prob.   C P C prob.
G G G pcp   G G G cpc
G G D pc(1-p)   G G D cp(1-c)
D G G (1-p)cp   D G G (1-c)pc

Total

 pc(2-p)  

Total

 pc(2-c)

 


Como es más probable que Elmer supere a su padre que al campeón,

p es mayor que c

y

2 - p es menor que 2 - c,

por lo que Elmer debería elegir C-P-C.

Por ejemplo, para p = 0,8, c = 0,4, la probabilidad de ganar el premio con PCP es 0,384, la de C-P-C es 0,512.

Por tanto, la importancia de ganar el segundo juego supera la desventaja de jugar dos veces contra el campeón.

Muchos de nosotros tendemos a suponer que cuanto mayor es el número esperado de éxitos, mayor es la probabilidad de ganar un premio y, a menudo, esta suposición resulta útil. Pero en ocasiones un problema tiene condiciones especiales que destruyen este razonamiento por analogía.

En nuestro problema, el número esperado de victorias bajo CPC es 2c + p,  menor que el número esperado de victorias para PCP, 2p + c.

En nuestro ejemplo con p = 0,8 y c = 0,4, estas medias son 1,6 y 2,0 en ese orden. Esta oposición de respuestas le da al problema su sabor. La idea de eventos independientes se explica en PWSA.

Para abordar la situación de manera que se intuya lógico optar por la secuencia C-P-C, consideremos que se disputan cuatro sets alternativos: primero contra el Campeón (C), luego contra su Padre (P), nuevamente contra el Campeón y finalmente contra su Padre. Podemos decidir de antemano si los tres primeros sets o los tres últimos contarán para el premio. La dinámica es similar a la del problema, y de todas las combinaciones posibles, las que otorgan premio solo con una opción y no con la otra son estos casos, los de la primera columna otorgan premio si se escoge CPC  y no lo otorgan con la opción PCP

1º set contra C G  
2º set contra P G D
3º set  contra C D G
4º set contra P   G

La segunda columna muestra los casos en los que Elmer ganaría premio si escoge PCP pero perdería si hubiera escogido CPC

Los casos de cada columna frente a los de la otra difieren en perder contra el Campeón (la primera), frente a perder contra su padre (la segunda) y es más probable perder contra el campeón de modo que a Elmer le interesa que empiece a contar como primer set uno jugado contra el campeón.

 

PROBLEMA 2

Elmer además de mirar la probabilidad de ganar el premio que le ofrece su padre también quiere considerar su esfuerzo, pue jugar un partido contra el campeón le supone más esfuerzo que jugarlo contra su padre.
¿Como podríamos cuantificar el esfuerzo de Elmer?
Podríamos decir que en cada juego el esfuerzo gane o pierda es inversamente proporcionar a la probabilidad de ganar al rival

Pongamos que el esfuerzo para jugar con C es 1/c (gane o pierda) y con su padre, 1/p

Construyamos la tabla del esfuerzo

Contra Padre 1º   Contra el Campeón 1º
P C P esf.   C P C esf.
      2/p+1/c         2/c+1/p

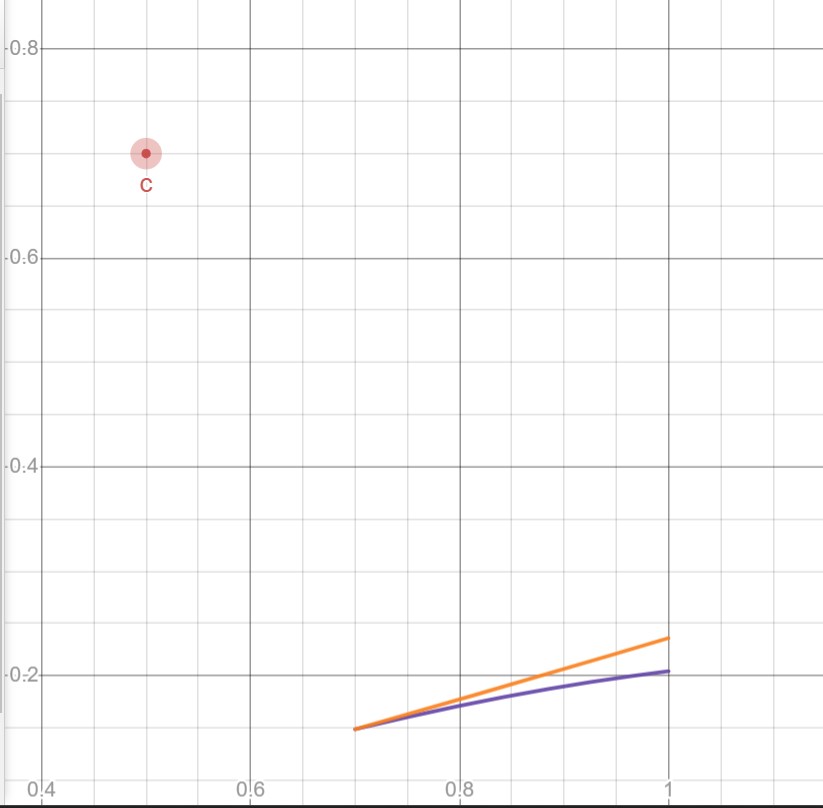
En la opción contra el Padre 1º el esfuerzo es

(2c+p)/pc

En la opción contra el Campeón 1º el esfuerzo es

(2p+c)/pc

Elmer quiere maximizar la probabilidad de ganar premio y minimizar el esfuerzo que le supone. Podríamos estudiar la función prob/esf en cada caso.

Comparar con qué estrategia es mayor el cociente prob/esf.

(2-p)(pc)2/(2c+p)   o    (2-c)(pc)2/(2p+c) 

https://www.desmos.com/calculator/lqetmczgzl

mueve el punto rojo para variar c
x en la gráfica es p

A Elmer según sean los valores de c y p  le interesa tomar la estrategia primero con C si es que la gráfica naranja va por encima de la azul, en los otros casos tomara la estrategia de comenzar con P, pues aunque tenga menos probabilidad de ganar, el esfuerzo va a ser menor

Dejamos dos capturas de cómo se comportan las dos curvas según dos valores de c


 

Por ejemplo cuando c=0,7 y p=0,9 , deberá empezar a jugar con el Campeón

Cuando c=0,1 y p=0,5 Elmer empezará contra su padre, pero

Hagamos algunos cálculos de la probabilidad de ganar el premio y el esfuerzo de Elmer

p c 1º prob esf 1º prob esf
0,5 0,1 P 0.075 14 C 0.095 22
0,9 0,7 P 0,693 3.65 C 0.819 3.97

En la hoja de cálculo se pueden ver estos valores y los de la función que hemos tomado para ayudar a Elmer a decidirse tomando la estrategia que

maximice prob/esf

En gris se señalan los casos en los que le recomendaríamos a Elmer jugar primero con el Campeón pues

prob de ganar el premio / esfuerzo

es mayor o igual empezando con el campeón que con su padre.
 

c p prob si 1º P esf si 1º P prob/esf prob si 1º C esf si 1º C prob/esf
0.1 0.2 0.036 20.000 0.002 0.038 25.000 0.002
0.1 0.3 0.051 16.667 0.003 0.057 23.333 0.002
0.1 0.4 0.064 15.000 0.004 0.076 22.500 0.003
0.1 0.5 0.075 14.000 0.005 0.095 22.000 0.004
0.1 0.6 0.084 13.333 0.006 0.114 21.667 0.005
0.1 0.7 0.091 12.857 0.007 0.133 21.429 0.006
0.1 0.8 0.096 12.500 0.008 0.152 21.250 0.007
0.1 0.9 0.099 12.222 0.008 0.171 21.111 0.008
0.1 1.0 0.100 12.000 0.008 0.190 21.000 0.009
0.2 0.3 0.102 11.667 0.009 0.108 13.333 0.008
0.2 0.4 0.128 10.000 0.013 0.144 12.500 0.012
0.2 0.5 0.150 9.000 0.017 0.180 12.000 0.015
0.2 0.6 0.168 8.333 0.020 0.216 11.667 0.019
0.2 0.7 0.182 7.857 0.023 0.252 11.429 0.022
0.2 0.8 0.192 7.500 0.026 0.288 11.250 0.026
0.2 0.9 0.198 7.222 0.027 0.324 11.111 0.029
0.2 1.0 0.200 7.000 0.029 0.360 11.000 0.033
0.3 0.4 0.192 8.333 0.023 0.204 9.167 0.022
0.3 0.5 0.225 7.333 0.031 0.255 8.667 0.029
0.3 0.6 0.252 6.667 0.038 0.306 8.333 0.037
0.3 0.7 0.273 6.190 0.044 0.357 8.095 0.044
0.3 0.8 0.288 5.833 0.049 0.408 7.917 0.052
0.3 0.9 0.297 5.556 0.053 0.459 7.778 0.059
0.3 1.0 0.300 5.333 0.056 0.510 7.667 0.067
0.4 0.5 0.300 6.500 0.046 0.320 7.000 0.046
0.4 0.6 0.336 5.833 0.058 0.384 6.667 0.058
0.4 0.7 0.364 5.357 0.068 0.448 6.429 0.070
0.4 0.8 0.384 5.000 0.077 0.512 6.250 0.082
0.4 0.9 0.396 4.722 0.084 0.576 6.111 0.094
0.4 1.0 0.400 4.500 0.089 0.640 6.000 0.107
0.5 0.6 0.420 5.333 0.079 0.450 5.667 0.079
0.5 0.7 0.455 4.857 0.094 0.525 5.429 0.097
0.5 0.8 0.480 4.500 0.107 0.600 5.250 0.114
0.5 0.9 0.495 4.222 0.117 0.675 5.111 0.132
0.5 1.0 0.500 4.000 0.125 0.750 5.000 0.150
0.6 0.7 0.546 4.524 0.121 0.588 4.762 0.123
0.6 0.8 0.576 4.167 0.138 0.672 4.583 0.147
0.6 0.9 0.594 3.889 0.153 0.756 4.444 0.170
0.6 1.0 0.600 3.667 0.164 0.840 4.333 0.194
0.7 0.8 0.672 3.929 0.171 0.728 4.107 0.177
0.7 0.9 0.693 3.651 0.190 0.819 3.968 0.206
0.7 1.0 0.700 3.429 0.204 0.910 3.857 0.236
0.8 0.9 0.792 3.472 0.228 0.864 3.611 0.239
0.8 1.0 0.800 3.250 0.246 0.960 3.500 0.274
0.9 1.0 0.900 3.111 0.289 0.990 3.222 0.307


 

 

CRÉDITOS

Fifty challenging problems in probability. Frederick Mosteller

Probabilidad y aplicaciones estadísticas Paul L. Meyer

Desmos calculator

Animación inicial con Chat GPT

 

Consolación Ruiz Gil Febrero 2024  https://www.matsolin.com/victorias/index.htm