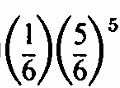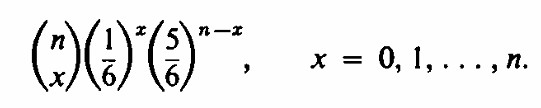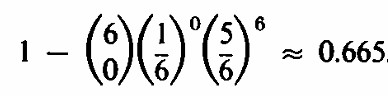Pepys escribió a Newton para preguntar cuál de los tres eventos es más probable:

que una persona obtenga

(a) al menos 1 seis cuando se lanzan 6 dados,

(b) al menos 2 seis cuando se lanzan 12 dados, o

(c) al menos 3 seis cuando se lanzan 18 dados.

¿Cuál es la respuesta?

Simulación

Sí, Samuel Pepys le escribió una larga y complicada carta a Isaac Newton sobre una apuesta que planeaba hacer.

Para decidir cuál opción era la favorable, Pepys necesitaba la respuesta a la pregunta anterior.

Puede que desee leer la correspondencia en American Statistician, Vol. 14, No. 4, Oct., 1960, pp . 27–30 , “ Samuel Pepys , Isaac Newton , y Probabilidad , "discusión por Emil D. Schell en "Preguntas y Respuestas , " editado por Ernest Rubin ; y comentario adicional en el númerodefebrero de 1961 , Vol . 15 , No. 1 , p . 29.

Hasta donde yo sé, esta es la única incursión de Newton en la probabilidad .

Dado que 1 es el número promedio o medio de seises cuando se lanzan 6 dados ,

2 el número promedio para 12 dados ,

y 3 el número promedio para 18 ,

uno podría pensar que las probabilidades de los tres eventos deben ser iguales .

Y muchos pensarían que es igual a 1/2.

Ese pensamiento sería otro ejemplo de confusión entre promedios y probabilidades .

Cuando el número de dados lanzados es muy grande, entonces la probabilidad de que el número de seises sea igual o mayor que el número esperado es ligeramente mayor que 1/2 .

Así que para un gran número de dados , la suposición es casi cierta , pero no para un número pequeño .

Para un gran número de dados,la distribución del número de seises es aproximadamente simétrica alrededor de la media, y el término en la media es pequeño, pero para un pequeño número de dados, la distribución es asimétrica y la probabilidad de obtener exactamente el número medio es sustancial.

Comencemos calculando la probabilidad de obtener exactamente 1 seis cuando se lanzan 6 dados.

La probabilidad de obtener 1 seis y 5 resultados diferentes en un or den específ ico es

Necesitamos multiplicar por el número de órdenes para 1 seis y 5 no seises.

En una división pareja al lanzar una moneda, problema 50 caras, aprendimos a contar el número de órdenes y obtenemos la probabilidad de exactamente C6,1=6, luego la probabilidad de un solo seis es

De manera similar, la probabilidad de exactamente x seises cuando se lanzan 6 dados es

Esta fórmula da los términos de lo que se llama una distribución binomial.

La probabilidad de obtener 1 o más seises con 6 dados es el complemento de la probabilidad de obtener 0 seises:

Cuando se lanzan 6n dados, la probabilidad de obtener n o más seises es

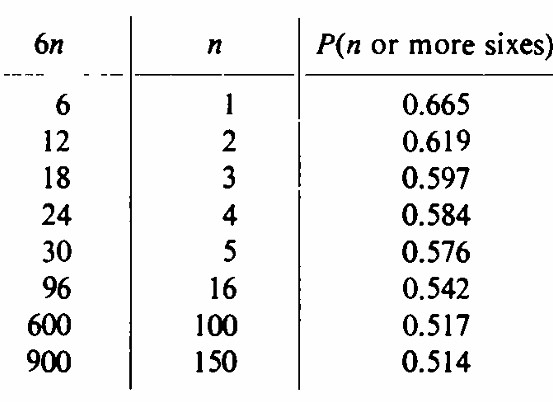
Desafortunadamente, Newton tuvo que calcular las probabilidades a mano, pero nosotros podemos usar las Tablas de la distribución binomial acumulativa, Harvard University Press, 1955. (Nosotros hoy contamos con wolfram mathemática, Mosteller con la tabla).

Nuestra tabla corta muestra las probabilidades, redondeadas a tres decimales, de obtener uno o más seises cuando se lanzan 6n dados.

 Claramente Pepys lo hará mejor con la apuesta de dados de 6 caras que con 12 o 18. Cuando se enteró de eso, decidió no cumplir con su apuesta original. La distribución binomial se trata extensamente en PWSA, Capítulo 7, ver espe cialmente pp. 241-257

Créditos
Traducción del problema 19 del libro Fifty challenging problems in probability , MOSTELLER

Vídeo introducción con lumen5.com