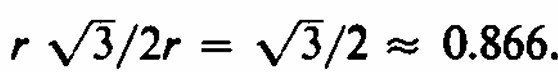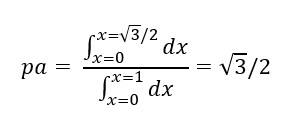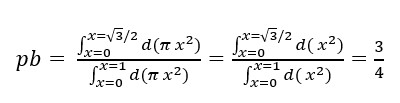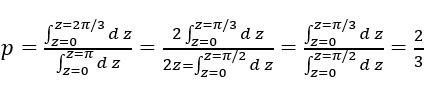|
Problema 25 del libro de Mosteller Longitudes de Cuerdas Aleatorias Si se selecciona al azar una cuerda en un círculo fijo, ¿cuál es la probabilidad de que su longitud supere el radio del círculo?
El libro explica así las soluciones Algunas Soluciones Plausibles Hasta que la expresión "al azar" se haga más específica, la pregunta no tiene una respuesta definitiva. Las tres suposiciones plausibles siguientes, junto con sus tres probabilidades diferentes, ilustran la incertidumbre en la noción de "al azar" que a menudo se encuentra en problemas de probabilidad geométrica. No podemos garantizar que ninguno de estos resultados coincida con los obtenidos de algún proceso físico que el lector pueda usar para elegir cuerdas al azar, de hecho, el lector puede disfrutar estudiando empíricamente si alguno coincide. Sea r el radio del círculo.
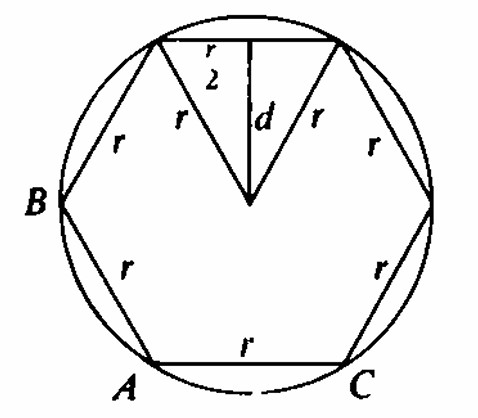
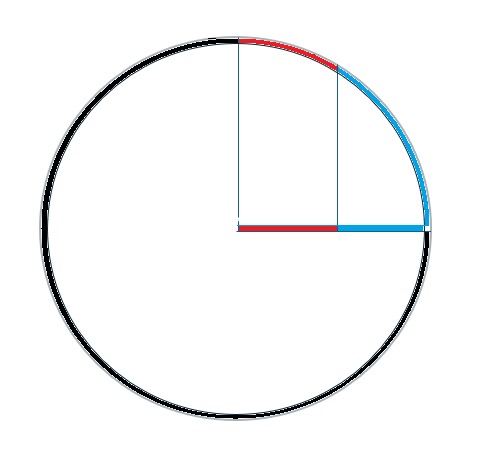
(a) Supongamos que la distancia de la cuerda desde el centro del círculo está distribuida uniformemente de 0 a r. Dado que se puede inscribir un hexágono regular de lado en un círculo, para obtener la probabilidad, simplemente encuentre la distancia d desde el centro y divida por el radio. Tenga en cuenta que d es la altura de un triángulo equilátero de lado r. Por lo tanto, desde la geometría plana obtenemos
Consecuentemente, la probabilidad deseada es
( b ) Supongamos que el punto medio de la cuerda está distribuido uniformemente en el interior del círculo . Consultando nuevamente la figura , vemos que la cuerda es más larga que el radio cuando el punto medio de la cuerda está a una distancia menor que d del centro . Así, todos los puntos en el círculo de radio d, concéntricos con el círculo original, pueden servir como puntos medios de la cuerda . Su fracción, en relación con el área del círculo original, es πd² / πr² = d² / r² = 0.75 . Esta probbilidad es el cuadrado del resultado que obtuvimos de la suposición ( a ) anterior . ( c ) Si con cada punto de la circunferencia consideramos las cuerdas que están en el arco de 180º a partir de él, tendremos todas las cuerdas. Y con cada punto las cuerdas que son menor que erl radio son las que abarcan menos de 60º, de modo que hay 60º para las que son menores y de 60 a 180º se definen las cuerdas que miden más que el radio, esto da un probabilidad de 2/3. Hasta aquí la traducción del libro de Mosteller, problema 25. El problema es una versión de la paradoja de Bertrand, en el enlace se puede ver publicado en su libro "Cálculo de probabilidades" (1889). Después de reflexionar sobre el problema se explica la conclusión
Quisiera poner énfasis en la distinción del azar escogido y la medida de probabilidad tomada, En (a) el azar está definido escogiendo aleatoriamente (a, b) donde "a" es un número entre 0 y 1, "b" entre 0 y 2п. Ese es el azar, sus representaciones pueden ser diferentes, y la medida de probabilidad que tomemos también, si con este azar representamos cuerdas y medimos radios, podemos definir los casos de cuerdas mayores que el radio=1 como la medida de ese radio límite , raíz(3)/2 , que al dividirla entre la medida del radio total nos da la probabilidad "pa" , esto es,
O podemos medir con el área,
La variable x en ambos casos es el parámetro "a", el radio, estoy tomando diferentes medidas con el mismo azar y salen proporciones diferentes. También podemos medir con el arcos(x) es decir, el arco que define el radio,
Hemos tomado en (a) diferentes medidas con un mismo azar, los casos (a) y (b) explican probabilidades "pa" y "pb" obtenidas con el mismo azar pero diferentes medidas. En (c) no se tomó el mismo azar que en "pc", en (c) tomamos un parámetro "a" entre 0 y п y otro parámetro b entre 0 y 2п, sus valores determinan un arco en la circunferncia. El arco de extremos (cos b, sen b) (cos (b+a), sen (b+a)) Para la medida en "p" tomamos la medida de los arcos, misma medida que en (a) con "pc" pero diferente azar.
z representa el parámetro "a"entre 0 y п . Comparando "p" con "pc", la diferencia es el cambio de variable, vemos que cambiar de azar es solo un cambio de variable, de x (entre 0 y 1) a z (entre 0 y п) y la probabilidad se conserva, ya que no hemos cambiado de medida.
Puede descargarse en pdf esta explicación
A continuación de añaden más casos y sus simulaciones caso (d) Con el mismo azar de (a), "a" es un valor entre 0 y 1 y "b" entre 0 y 2pi Con "b" fijo, por ejemplo b=0 y "a" entre y raíz(3)/2 y 1, y considerando que (a, b) define el centro de las cuerdas, estas rellenan un casquete, tomaremos la probabilidad de que "a" mayor que raíz(3)/2 como el área de ese casquete entre el área del casquete total (de áreza pi/2)
el área del casquete que definen estas cuerdas rojas es 1/2 · ( pi/3- raíz(3)/2) el área del casquete total es pi/2 La probabilidad de que las cuerdas sean mayor que 1 es el cociente de pi/2-1/2 · ( pi/3- raíz(3)/2) entre pi/2
Por si teníamos pocos resultados para esta probabilidad, uno más
Similemos diferentes medidas con el mismo azar de (a) SIMULACIÓN CON CHATGPT DE (a) Se ajusta su probailidad a (b), (c) y (d) Lo que produce estas diferencias se puede explicar con esta simulación, aquí el azar es igual en pa, pb, pc y pd, pero pb, pc, y pd llevan ajustes que explicamos después, primero veamos que funciona, pa=raíz(3)/2, pb=3/4, pc=2/3, pd=0,943 aprox
Explicamos el código de la escena, se escogen aleatoriamente los valores de a entre 0 y 1 y b entre 0 y 2pi y se dibuja el punto P a(cos(b), sen(b)) centro de una cuerda, la perpendicular a PC que pasa por P, siendo C el centro de la circunferencia. Se ve dibujada la última cuerda, o sea, la correspondiente al último punto P o centro. Si la cuerda es mayor que el radio se añade uno al valor de M, es decir, M cuenta las cuerdas mayores que el radio. Los puntos escogidos si dan longitud de cuerda mayor que el radio se pintan de rojo, sino de azul. En el texto "pa"es el cociente M/Cuerdas. O sea la probabilidad según (a) "pb" es esa probabilidad ponderada por áreas, se ha dividido el circulo en 1000 coronas concéntricas según distintos valores de "a" por milésimas. Está claro que si tomamos m[i] como el número de puntos que nos salen aleatoriamente al escoger "a" y "b" en la corona i, al hacer el experimento muchas veces estos 1000 valores son muy similares, y sin embargo el área de las coronas no, entonces se multiplica cada m[i] por 2i+1 ya que el área de esa corona es el área de la corona de m[0] por 2i+1, y para que la probabilidad total sea 1 tenemos que dividir por m[0]1+m[1]3+m[2]5+...+m[999]19999, p= (suma de m[i]·(2i+1)) cuandoi=0,1,...8660 dividido por (esa suma, cuando i=0,1,...999) En realidad pb es el cociente Suma de los m[i]·diferencias (áreas coronas), i de 0 a 8660 entre Suma de los m[i]·diferencias (áreas coronas) i de 0 a 10000 es decir , en el límite , un cociente de integrales, ponderando el cambio
Nota: "pa" es lo mismo pero con dx, en pb al considerar coronas pues las diferencias (con el cociente) quedan dx2 o diferencias de áreas. Con esta ponderación pb =probabilidad del caso (b)
Para el cálculo de "pc" hemos tenido en cuenta que en (a, b) si
dejamos "a" ajustado a las milésimas entre una milésima y otra, todos los
(i/10000, b) diferen en una milesima de los ((i+1)/10000, b) pero en su
representación real los (i/10000, b) son las cuerdas con extremo en el arco de
coseno i/10000, los ((i+1)/10000, b) son las cuerdas con extremo en el arco de
coseno (i+1)/10000 m[i] * (1 / Math.sqrt(1 - (i / 10000) ** 2)) ya que d(acosx)= dx Los valores de a son de longitudes, y cada intervalo de esa longitud se pondera así para que se corresponda con el intervalo que determinan esas cuerdas en la representación en el arco. Con esta ponderación pc es la probabilidad del caso (c)
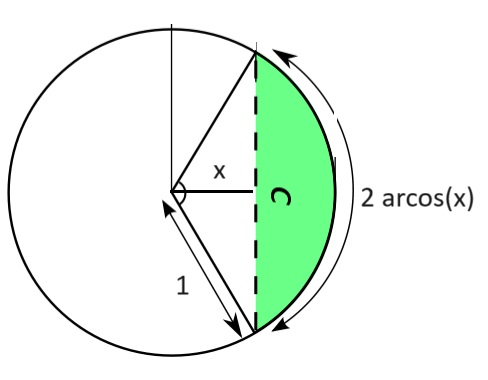
En (d) las diferencias son d(A(x)), siendo A(x) el área del casquete verde de la figura siguiente, por eso en el código para calcular pd se han puesto las sumas de m[i] *2* Math.sqrt(1 - (i / 10000)**2) ya que A(x)=arcos(x)-sen(arcos(x)), el área del casquete
A(x)'= Esta probabilidad pd es la que sale en el caso (d) vemos que también sale con (a) al ponderar según d(A(x)) , es decir las diferencias de las áreas de los sectores.
En los cuatro casos el azar ( parámetros elegidos ) es el mismo pero la función de distribución que define la probabilidad es diferente.
Caso (e) Con a entre 0 y 1 y b entre o y 2pi se define un punto de
la circunferencia de radio 1 y un radio “a” con estos datos hay dos cuerdas con
centro en la de radio a y un punto (cos b, sen b) De esta manera el mismo azar (a) lleva su resultado al
extremo de una cuerda. La longitud de la cuerda en función de a y b es 2
raiz(1-a^2), tenemos el mismo azar de (a) pero en lugar de calcular centros
calculamos extremos de cuerdas.
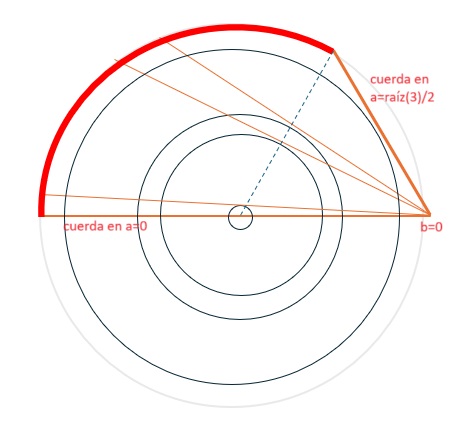
Para definir la probabilidad nos fijamos para a entre 0 y raíz(3)/2 que son los valores que dan una cuerda de longitud mayor que 1 . Para un b fijo , por ejemplo 0, si se toman los valores de "a" entre 0 y raíz(3)/2 obtenemos el otro punto de la cuerda (cuerdas rojas) en el arco rojo que abarca una longitud de 120º
por tanto los casos favorables a cuerdas mayores que la unidad abarcan un arco de longitud 2pi/3, mientras que los posibles abarcan un arco de longitud pi. Probabilidad 2/3.
A continuación dejamos la simulación del caso (c) con el azar diferente al de (a), vemos que su probabilidad coincide con la probabilidad "pc" anterior. SIMULACIÓN CON CHATGPT DE (c)
Explicamos el código de la escena, se escogen aleatoriamente los valores de a entre o y 2pi y b entre 0 y pi y se dibuja la cuerda de extremos (cos(a), sen(a)) y (cos(a+b), sen(a+b)) . Se toma la distancia d entre estos dos puntos Si d es mayor que el radio se añade uno al valor de M, es decir, M cuenta las cuerdas mayores que el radio. En el texto inferior P es el cociente M/Cuerdas.
Por seguir la misma nomenclatura de las variables pongamos que a entre 0 y pi y b entre 0 y 2pi, esto es lo que define el azar en (c), y vamos a compararlo con pc, ahí el azar estaba definido por a entre 0 y 1 , b entre 0 y 2pi
Agradecimientos
El problema es muy interesante. Agradezco al Catedrático de estadística Dr.
Cuesta Albertos sus explicaciones, y su paciencia escuchando siempre cualquier
comentario.
También agradezco las indicaciones del profesor D Pedro
Arias Castanedo que nos ha proporcionado este documento
de la web (original en inglés).
Créditos
Vídeo introducción con
lumen5.com
Simulación realizada por chatGPT
Consolación Ruiz Gil Abril 2024
https://www.matsolin.com/cuerdas/index.htm
|